
同,即1C(s) =TS +1这时相同的输出称为脉冲响应记作g(t),因为g()=L-[G(s)],其表达式为letc(t) = -1≥0(3-5)T3.2.3一阶系统的单位斜坡响应Unit-ramp Response of first-order Systems1当 R(s) =S?T211T1C(s) = Φ(s)R(s) =TS+1'522S1+ TS对上式求拉氏反变换,得:)=1-T+Te7c(t)=t-T(1-eT(3-6)因为e(1)=r(t)- c(t)= T(1-e(3-7)r(t) c(t)4r(t)c(t)←t01图3-5一阶系统的斜坡响应所以一阶系统跟踪单位斜坡信号的稳态误差为es=lime(t)=T上式表明:①一阶系统能跟踪斜坡输入信号。稳态时,输入和输出信号的变化率完全相同 r(t)=1 ,c(t)=1054
54 同,即 1 1 ( ) + = TS C s 这时相同的输出称为脉冲响应记作 g(t),因为 ( ) [ ( )] 1 g t L G s − = ,其表达式为 0 1 ( ) = − e t T c t T t (3-5) 3.2.3 一阶系统的单位斜坡响应 Unit-ramp Response of first-order Systems 当 2 S 1 R(s) = TS T S T TS S S C s s R s + = − + + = = 1 1 1 1 1 ( ) ( ) ( ) 2 2 2 对上式求拉氏反变换,得: t T t T c t t T e t T Te 1 1 ( ) (1 ) − − = − − = − + (3-6) 因为 ( ) ( ) ( ) (1 ) 1 t T e t r t c t T e − = − = − (3-7) r(t) c(t) r(t) c(t) t 0 图 3-5 一 阶 系 统 的 斜 坡 响 应 所以一阶系统跟踪单位斜坡信号的稳态误差为 e e t T t ss = = → lim ( ) 上式表明:①一阶系统能跟踪斜坡输入信号。稳态时,输入和输出信号的变化率完全相 同 ( ) = 1 , ( ) = 1 → t r t c t

②由于系统存在惯性,c(t)从0上升到1时,对应的输出信号在数值上要滞后于输入信号一个常量T,这就是稳态误差产生的原因。③减少时间常数T不仅可以加快瞬态响应的速度,还可减少系统跟踪斜坡信号的稳态误差。3.2.4一阶系统的单位加速度响应1T1r(t) =R(s) =S3S+2TT2T2BcDT111AC(s) = Φ(s)R(s) =52s152153S3S3TS+1sS+S+TTc(t) =2-Tt+T(1-(t≥0). (3 8)-ee(t)=r(t)-c(t)= Tt-T2(1-eT (3 8)上式表明,跟踪误差随时间推移而增大,直至无限大。因此,一阶系统不能实现对加速度输入函数的跟踪。表3-1一阶系统对典型输入信号的响应式输入信号输出响应传递函数1o*8(t)1(t≥0)微微分分11(t)1-et≥0s1t11ttt-T+TeT1≥0S2TS+11!P-Tt+T?(1-e)1≥0-S32等价关系:系统对输入信号导数的响应,就等于系统对该输入信号响应的导数:系统对输入信号积分的响应,就等于系统对该输入信号响应的积分:积分常数由零初始条件确定。线性定常系统的一个重要特性,适用于任何阶线性定常系统,但不适用于线性时变系统55
55 ②由于系统存在惯性, c(t) 从 0 上升到 1 时,对应的输出信号在数值上要滞 后于输入信号一个常量 T,这就是稳态误差产生的原因。 ③减少时间常数 T 不仅可以加快瞬态响应的速度,还可减少系统跟踪斜坡信 号的稳态误差。 3.2.4 一阶系统的单位加速度响应 2 2 1 r(t) = t 3 1 ( ) S R s = T S T 1 1 + T S T S T S T S T S D S C S B S A TS S C s s R s 1 1 1 1 ) 1 1 ( ) ( ) ( ) ( 2 2 3 3 2 3 2 + = − + − + = + + + + = = (1 ) ( 0) (3 8) 2 1 ( ) 1 2 2 = − + − − − c t t Tt T e t t T ( ) ( ) ( ) (1 ) (3 8) 1 2 = − = − − − − t T e t r t c t Tt T e 上式表明,跟踪误差随时间推移而增大,直至无限大。因此,一阶系统不能实现对加速 度输入函数的跟踪。 表 3-1 一阶系统对典型输入信号的响应式 输入信号 输出响应 传递函数 微 分 (t) 1 ( 0) 1 − e t T T t 微 分 1 1 TS + 1(t) S 1 1− 0 − e t T t t 2 1 S − + 0 − t T Te t T t 2 2 1 t 3 1 S (1 ) 0 2 1 2 2 − + − − t Tt T e t T t 等价关系:系统对输入信号导数的响应,就等于系统对该输入信号响应的导数; 系统对输入信号积分的响应,就等于系统对该输入信号响应的积分;积分常 数由零初始条件确定。 线性定常系统的一个重要特性,适用于任何阶线性定常系统,但不适用于线性时变系统
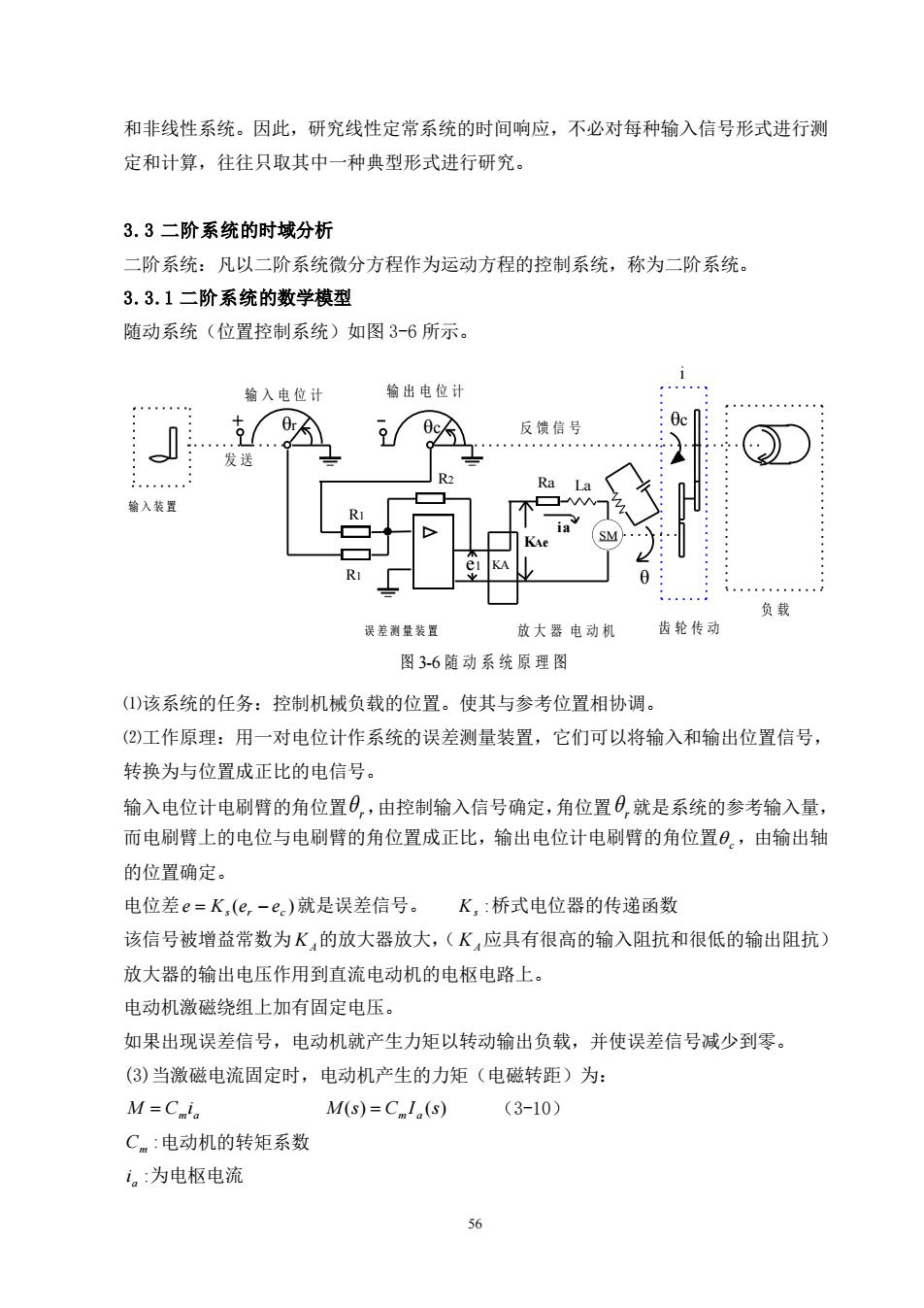
和非线性系统。因此,研究线性定常系统的时间响应,不必对每种输入信号形式进行测定和计算,往往只取其中一种典型形式进行研究。3.3二阶系统的时域分析二阶系统:凡以二阶系统微分方程作为运动方程的控制系统,称为二阶系统。3.3.1二阶系统的数学模型随动系统(位置控制系统)如图3-6所示。输出电位计输入电位计Ocec反馈信号aT发送R2Ra输入装置RIKAKAelR1aD负载齿轮传动误差测量装置放大器电动机图3-6随动系统原理图(1)该系统的任务:控制机械负载的位置。使其与参考位置相协调。(2)工作原理:用一对电位计作系统的误差测量装置,它们可以将输入和输出位置信号,转换为与位置成正比的电信号。输入电位计电刷臂的角位置,由控制输入信号确定,角位置就是系统的参考输入量,而电刷臂上的电位与电刷臂的角位置成正比,输出电位计电刷臂的角位置。,由输出轴的位置确定。电位差e=K,(e,-e.)就是误差信号。K,桥式电位器的传递函数该信号被增益常数为K,的放大器放大,(K应具有很高的输入阻抗和很低的输出阻抗)放大器的输出电压作用到直流电动机的电枢电路上。电动机激磁绕组上加有固定电压。如果出现误差信号,电动机就产生力矩以转动输出负载,并使误差信号减少到零。(3)当激磁电流固定时,电动机产生的力矩(电磁转距)为:M=CmiaM(s)=CmI.(s)(3-10)Cm:电动机的转矩系数i。:为电枢电流56
56 和非线性系统。因此,研究线性定常系统的时间响应,不必对每种输入信号形式进行测 定和计算,往往只取其中一种典型形式进行研究。 3.3 二阶系统的时域分析 二阶系统:凡以二阶系统微分方程作为运动方程的控制系统,称为二阶系统。 3.3.1 二阶系统的数学模型 随动系统(位置控制系统)如图 3-6 所示。 + 图 3-6 随 动 系 统 原 理 图 输 入 电 位 计 输 出 电 位 计 θr θc 发 送 反 馈 信 号 SM θc ia 输 入 装 置 e1 KA KAe La R1 R1 R2 θ i 放 大 器 电 动 机 齿 轮 传 动 负 载 误 差 测 量 装 置 Ra ⑴该系统的任务:控制机械负载的位置。使其与参考位置相协调。 ⑵工作原理:用一对电位计作系统的误差测量装置,它们可以将输入和输出位置信号, 转换为与位置成正比的电信号。 输入电位计电刷臂的角位置 r ,由控制输入信号确定,角位置 r 就是系统的参考输入量, 而电刷臂上的电位与电刷臂的角位置成正比,输出电位计电刷臂的角位置 c ,由输出轴 的位置确定。 电位差 ( ) s r c e = K e − e 就是误差信号。 : Ks 桥式电位器的传递函数 该信号被增益常数为 KA 的放大器放大,( KA 应具有很高的输入阻抗和很低的输出阻抗) 放大器的输出电压作用到直流电动机的电枢电路上。 电动机激磁绕组上加有固定电压。 如果出现误差信号,电动机就产生力矩以转动输出负载,并使误差信号减少到零。 (3)当激磁电流固定时,电动机产生的力矩(电磁转距)为: m a M = C i M(s) C I (s) = m a (3-10) : Cm 电动机的转矩系数 : a i 为电枢电流
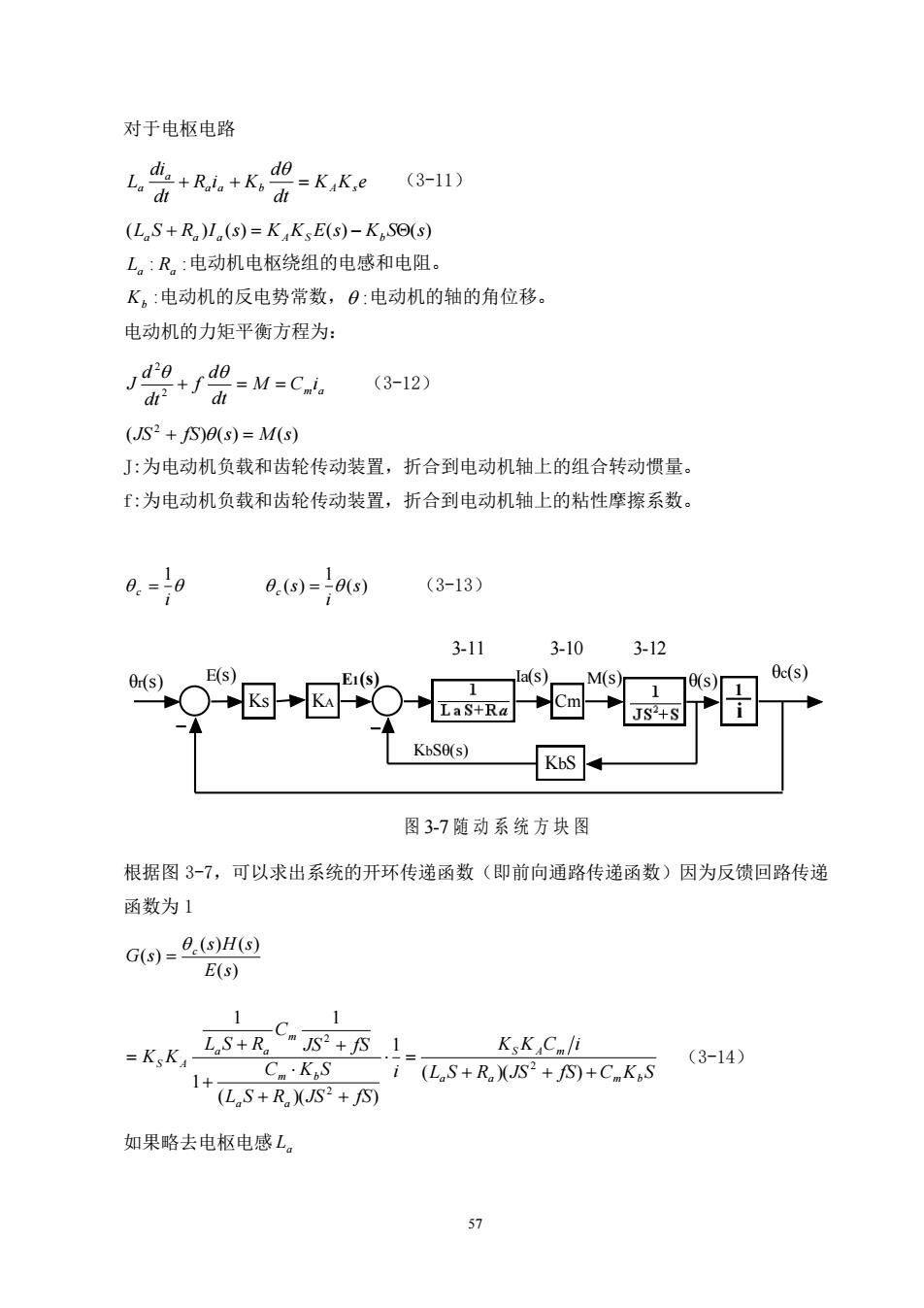
对于电枢电路dia+Ria+KpdeL(3-11)=K,K,edtdt(L,S+R)I.(s)=K K,E(s)-K,SO(s)L。:R:电动机电枢绕组的电感和电阻。K,:电动机的反电势常数,9:电动机的轴的角位移。电动机的力矩平衡方程为:derde=M=Cmia(3-12)+fdt?dt(JS? + fS)O(s) = M(s)J:为电动机负载和齿轮传动装置,折合到电动机轴上的组合转动惯量。f:为电动机负载和齿轮传动装置,折合到电动机轴上的粘性摩擦系数。0.(s) :(3-13)0(s)H73-113-103-120c(s)E(s)la(s)M(s)E1(s)Or(s)0(s)111HKsKsCm-LaS+RaiJS*+sKbSe(s)Kbs图3-7随动系统方块图根据图3-7,可以求出系统的开环传递函数(即前向通路传递函数)因为反馈回路传递函数为10.(s)H(s)G(s) = E(s)1JS? + fSL,S+R.K,K,Cm/i(3-14)=K,KC.K,S(L.S+R.)(JS2 + fS)+C.K,S1+(L,S+ R.)(JS? + JS)如果略去电枢电感L。57
57 对于电枢电路 K K e dt d R i K dt di L a a b A s a a + + = (3-11) (L S R )I (s) K K E(s) K S (s) a + a a = A S − b : : La Ra 电动机电枢绕组的电感和电阻。 : Kb 电动机的反电势常数, : 电动机的轴的角位移。 电动机的力矩平衡方程为: m a M C i dt d f dt d J + = = 2 2 (3-12) ( ) ( ) ( ) 2 JS + fS s = M s J:为电动机负载和齿轮传动装置,折合到电动机轴上的组合转动惯量。 f:为电动机负载和齿轮传动装置,折合到电动机轴上的粘性摩擦系数。 i c 1 = ( ) 1 ( ) s i s c = (3-13) Ks KA Cm i 1 KbS θr(s) E(s) E1(s) Ia(s) M(s) θ(s) θc(s) 3-11 3-10 3-12 KbSθ(s) 图 3-7 随 动 系 统 方 块 图 根据图 3-7,可以求出系统的开环传递函数(即前向通路传递函数)因为反馈回路传递 函数为 1 ( ) ( ) ( ) ( ) E s s H s G s c = L S R JS f S C K S K K C i i L S R JS f S C K S JS f S C L S R K K a a m b S A m a a m b m a a S A + + + = + + + + + = ( )( ) 1 ( )( ) 1 1 1 2 2 2 (3-14) 如果略去电枢电感 La
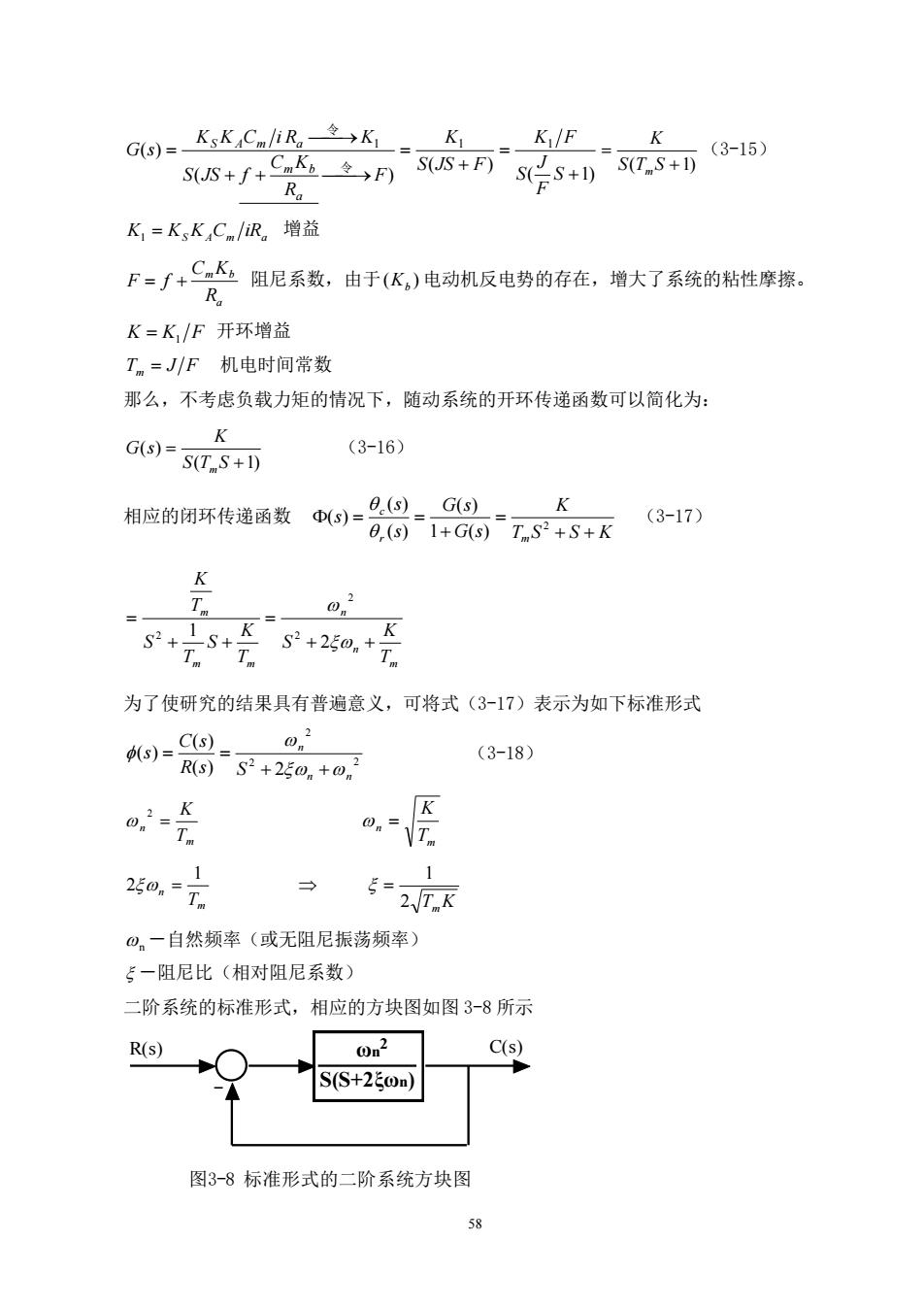
令K,K,K.Cm/iR>K,K,/FK(3-15)G(s) =CmKSyS(JS + F)S(T.S+1)→F)S(JS + f +S+1)RaFK,=K,K,Cm/iR。增益F=f+CmK,阻尼系数,由于(K,)电动机反电势的存在,增大了系统的粘性摩擦。R.K=K/F开环增益T,=J/F机电时间常数那么,不考虑负载力矩的情况下,随动系统的开环传递函数可以简化为:K(3-16)G(s) =S(T.S+I)K0,(s)G(s)相应的闭环传递函数(3-17)(s) =1+G(s)T.S?+S+K0,(s)K03T.S+KK-S+S?+250,+TmTmTm为了使研究的结果具有普遍意义,可将式(3-17)表示为如下标准形式a?C(s)d(s) =(3-18)R(s)$?+250,+02Ko-KO.VT.T.11L5=250, =Tm2/TKの.一自然频率(或无阻尼振荡频率)5一阻尼比(相对阻尼系数)二阶系统的标准形式,相应的方块图如图3-8所示On?C(s)R(s)S(S+260n)图3-8标准形式的二阶系统方块图58
58 ( 1) ( ) ( ) ( ) 1 1 1 + = + = + + ⎯⎯→ ⎯⎯→ = S F J S K F S JS F K F R C K S JS f K K C i R K G s a m b S A m a 令 令 ( +1) = S T S K m (3-15) S A m a K1 = K K C iR 增益 a m b R C K F = f + 阻尼系数,由于 ( ) Kb 电动机反电势的存在,增大了系统的粘性摩擦。 K = K1 F 开环增益 Tm = J F 机电时间常数 那么,不考虑负载力矩的情况下,随动系统的开环传递函数可以简化为: ( 1) ( ) + = S T S K G s m (3-16) 相应的闭环传递函数 T S S K K G s G s s s s r m c + + = + = = 2 1 ( ) ( ) ( ) ( ) ( ) (3-17) m n n m m m T K S T K S T S T K + + = + + = 2 1 2 2 2 为了使研究的结果具有普遍意义,可将式(3-17)表示为如下标准形式 2 2 2 ( ) 2 ( ) ( ) n n n R s S C s s + + = = (3-18) m n T K = 2 m n T K = m n T 1 2 = 2 Tm K 1 = n -自然频率(或无阻尼振荡频率) -阻尼比(相对阻尼系数) 二阶系统的标准形式,相应的方块图如图 3-8 所示 S(S+2ξωn) ωn R 2 (s) C(s) 图3-8 标准形式的二阶系统方块图 _