
0<5<1时,亦可用1,=1+0.75(书3-20)(3-27)On(2)②t,(上升时间)h(t,)=1 ,求得o sin(ot, +β)=0/1-at,+β=π, =元-β(3-31书)(3-28)Od一定,即β一定,→の,个→t,响应速度越快(3)③t,(峰值时间)对式(3-21)(书3-14)求导,并令其为零,求得Eone-5o sin(Oat+ β)-Oae cos(0at+ β) = 0Vi-5?Vi-52tg(oat+β)= : tgβ=A5at,=0,元,2元,…,根据峰值时间定义,应取0,=元,=-12元_1(3 - 29)(书3-22)T0d20d2一定时,の,个(闭环极点离负实轴的距离越远)→t,(4)④%orM,的计算,超调量超调量在峰值时间发生,故h(t,)即为最大输出1e-5odp sin(Oatp + β)h(tp)=1-Vi-22h(t,)=1+e""/N-:sin(元+β)=-sinβ=-/1-≤2h(tp)- h(o0)2×100%=e×100%0%=(3-30)(书3-23)h(o)64
64 0 1 时,亦可用 n d t 1+ 0.7 = (3-27) (书 3-20) ⑵ r t (上升时间) h(t r ) =1 ,求得 sin( ) 0 1 1 2 + = − − d r t e t n d t r + = d r t − = (3-28) (3-31 书) 一定,即 一定, →n →t r ,响应速度越快 ⑶ (峰值时间) p t 对式(3-21)(书 3-14)求导,并令其为零,求得 sin( + ) − cos( + ) = 0 − e t e t d t d d t n n n 2 1 ( ) − tg d t + = 2 1− tg = = 0,,2, d p t ,根据峰值时间定义,应取 d t p = (3 29) 2 2 1 2 1 = = = d − d d t p T (书 3-22) 一定时,n (闭环极点离负实轴的距离越远)→t p ⑷ % or M p的计算,超调量 超调量在峰值时间发生,故 ( ) p h t 即为最大输出 sin( ) 1 1 ( ) 1 2 + − = − − d p t p h t e t n p 2 1 ( ) 1 − − h t = + e p 2 sin( + ) = −sin = − 1− 100% 100% ( ) ( ) ( ) % 2 1 = − = − − e h h t p h (3-30) (书 3-23)
10090807060雪辉5040302010n00.10.20.30.40.50.60.70.80.9阻尼比图3-14§C(s)OnR(s) $? +250,S+0,25=0时,%=100%=0.4时,%=25.4%5=1.0时,0%=0当=0.4~0.8时%=1.5%~25.4%(5)③调节时间t,的计算典型二阶系统欠阻尼条件下的单位阶跃响应h(t) =1-e- sin(oat+ β)1≥0V1-52书式(3-14)βB=arctg= arccos5令^表示实际响应于稳态输出之间的误差,则有111(In+ IntsEOn△5Vi-65
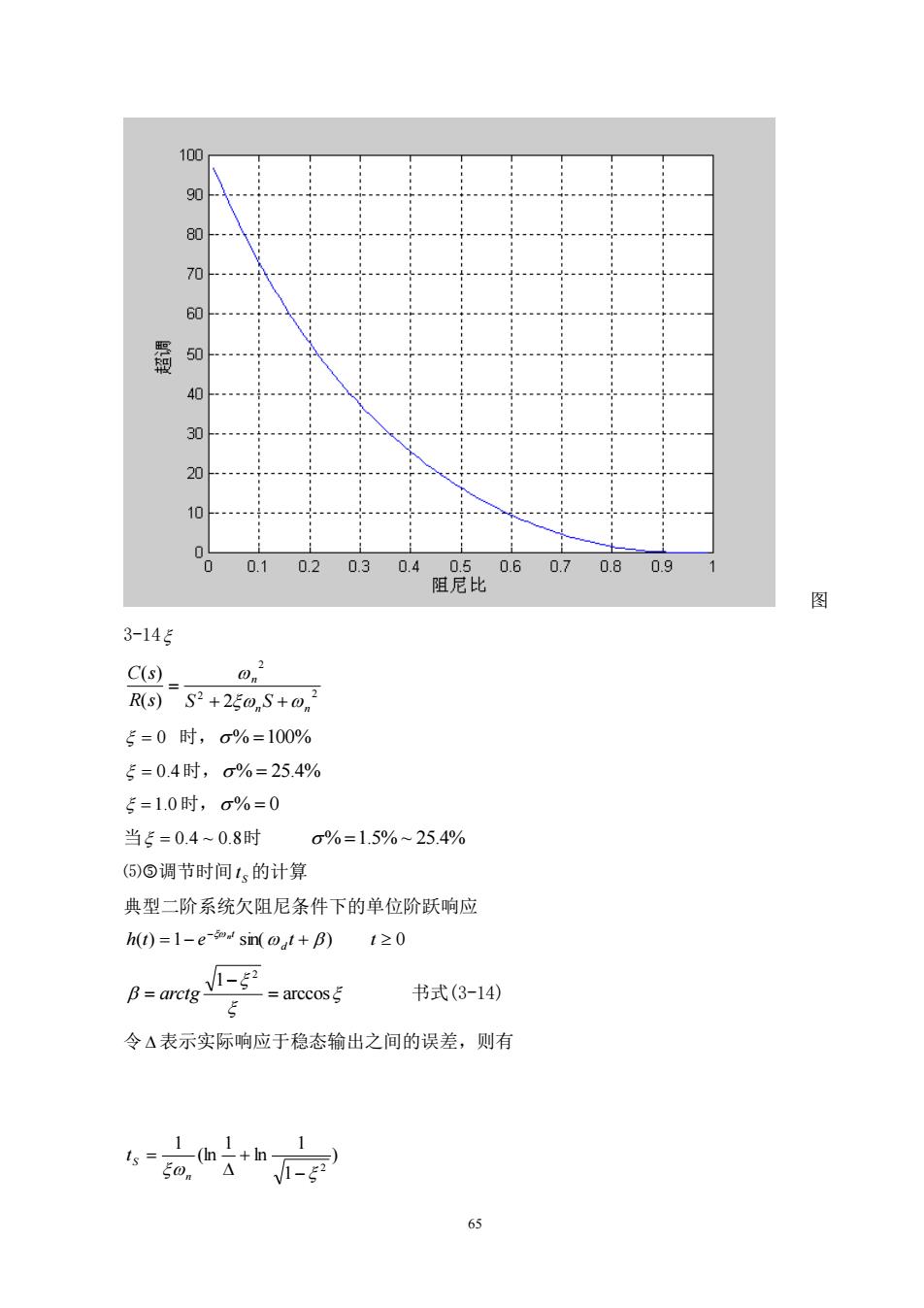
65 图 3-14 2 2 2 ( ) 2 ( ) n n n R s S S C s + + = = 0 时, % =100% = 0.4 时, % = 25.4% = 1.0 时, % = 0 当 = 0.4 ~ 0.8 时 % =1.5% ~ 25.4% ⑸调节时间 S t 的计算 典型二阶系统欠阻尼条件下的单位阶跃响应 ( ) = 1− sin( + ) 0 − h t e t t d t n arccos 1 2 = − = arctg 书式(3-14) 令 表示实际响应于稳态输出之间的误差,则有 ) 1 1 ln 1 (ln 1 2 − + = n S t