
12运动方程 21 前面将相空间区分为 4-空间(基中相点代表一 个分子的运动状态),它是 6(=2×3)维的相空间和 T-空间(其中相点代表由 N个粒子组成的体系的运 动状态),它是6N(=2× P 3V)维相空间。因此,一 图1,15 般地说,对自由度为f 的体系,相空间是2f维的空间影含N个分了时,∫=3N,故是 6N维的相空间,它的体积元为: dr=(dqidq,dqadp:dpadps) (dqadqsdgodp dpsdps).. (dqasdqawdqaspaxd Pas-d pas) (1.60)

第二章统计系综和Liouville定理 统计力学研究的体系包含着大量粒子(~10之8个),个别 分子的运动状态与整个体系的宏观性质不是简单地加合关系, 大量粒子的集会体产生了新的运动规律。所以要想确切地知道 每个分子运动状态是不可能的,即使知道每个分子的运动状态, 也无法准确地描述体系的运动状态。因此,不能沿用传统的经 典力学解微分运动方程的办法,而是根据概率理论,用统卧方 法求微观量的统计平均值 我们知道,已知某体系的宏观性质是在一定条件下对该体 系多次观测值的平均结果。每一·次观测是在宏观上很短时间内 进行的,而从微观上看,这个时闻是很长的。因此,每-…个观 测值是微观性质在其微观上长时间内的平均值。在此徽观长时 间内,体系的微观状态已经有了很多次的变化,则每一次观测 的结果儿乎就是…切可能微观状态的平均结果。所以,统计力 学中所求的平均值不是对时间求平均,而是在-·定宏观条件下 对一切可能微观状态的平均值。在求平均值时,各种微观状态 出现的几率可能不同。假设有一个处在不同微观状态体系的集 合,则可以就这个集合对体系进行几率描述。这就需要引入统 计系综的概念

$2,1统计系综和相密度 23 §2,1统计系综和相密度 己知在相空间中的代表点是表示所讨论体系的微观状态 的。如果把每个代表点看成一个力学体系时,则将相空间中这 些代表点的总和叫做统计系综。所以统计系综是由大量的性质 完全相同而各处于不同微观运动状态的力学体系所组成的。这 个定义表明,统计系综是研究力学体系所有可能运动状态总和 的-种形象化概念。它是相似休系的集合。 例如,研究某个体系,对它进行观测时,就相当于对它摄 一部电影。影片上显示出它经历的各种微观状态的画面.一次 观测结果是各个镜头画面一微观状态的平均值。-·个宏观性 质是次观硎的平均值,相当于这种部影片的平均效果. 在统计系综中,有”个性质相同的体系,各用矿个电影 机对准系综中?个体系拍摄,就得到P部影片。这样就得到 系综中各体系的全部观测结果。对于体系在t时划的统计描 述,可由观察犷部影片在t时刻的全部镜头画面得知。由于 ”料当大,在1时刻的个镜头就代表了体系随时间发生的 一切变化, 如果每个镜头画面代表体系的一种微观状态,在·时刻, 系综巾的”个体系就有”个镜头画面分别代表这些体系所处 的各种微观状态.各种微观快态出现的儿率不同。这样即可得 到统计系综中出现某-一个特殊结果的几率。虽然对单个体系的 行为不能预言,但是可以导出整个系综的统计行为。 在T空间中,体系的运动状态和相点是一一对应的,系 综中的个体系的运动状态,就有r个相点.个相点在相
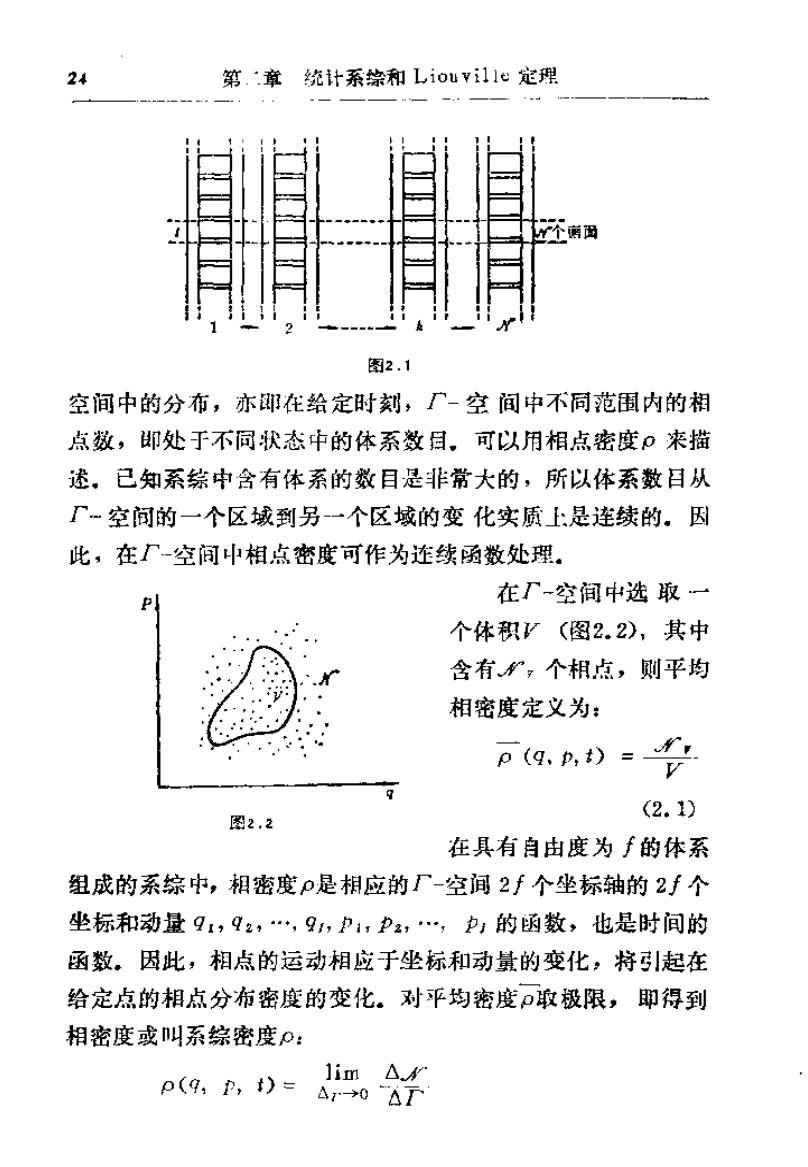
24 第.∴章统计系综和Liouvil1e定理 图2.1 空间中的分布,亦在给定时刻,-空间中不同范围内的相 点数,邯处于不同状态中的体系数目,可以用相点密度·来描 述。已知系综中含有体系的数目是非常大的,所以体系数目从 一空间的一个区域到另一个区域的变化实质上:是连续的。因 此,在厂-空间中相点密度可作为连续函数处理。 在T一空间中选取一 个体积V(图2.2),其中 含有,个相点,则平均 相密度定义为: p(9、p,t)=r (2.1) 图2.2 在具有自由度为∫的体系 组成的系综中,相密度·是相应的厂-空间2手个坐标轴的2f个 坐标和动量9,92,·,9,p1,p2…,;的函数,也是时间的 函数,因此,相点的运动相应于坐标和动量的变化,将引起在 给定点的相点分布密度的变化。对平均密度ρ取极限,即得到 相密度或叫系综密度P: 1im△ p(g,卫,=4r0△T

$2,1统计系综和相密度 25 (2.2) 因此P(9,力,)的物理意义是,在程9,…,9,卫1,…,p表示的 点,更确切地,即在厂-空间的无限小区城内找到体系数目的 度量.这个小区域是坐标位于g1和q:+d9:,92和g2+d92,…, 9,和9:+d9!之间和动量位于p1和p1+dp:,p2和p2+dp2, …,P5和p+dp之间的··个区域,其体积元为: dT=dg,dq2…dq dp:dp2…dpr (2.3) 则该休积元中的体系数且d为: dr=pdg,dgz…dq;dp,dp2…dpi (2.4) 或简记为: df”=pd9dp-pT 在统计系综中体系的总数是很大的,因此从厂-空间的一个区 域到另·个区城时,1d纩都可以认为是连续变化的。所以 系综中体系总数“可刑下列积分求得: f=∫dr=∫oddp=∫nodr (2.5) 式中积分号下标T表示对整个相空间求积分。 在T-空间中,”个相点出现在体积元dT内的几率为: drpdr=j(q.p.dr (2.6) 式中 f(9,p、t)sp/r (2.7) 称为相点的几率度或系综分布函数。将(2.7)式代人(2.5) 式,得 er-frrrfr 则 fdr=1 (2.8)