
16 第一章相空间及amilton方程 这里的考察适用所有的遵守经典力学的体系。在经典力学 中,能量是可以连续变化的。因此,由各能量决定的相迹便可 一条紧挨-一条地布满整个相空间。如果有一个孤立体系,它在 相空间的相点就必然作:恒定能量的表面上运动. 对·编谐振子,其二阶微分运动方程式(1.21) F,=i- d2x dia 可以化简为个一阶分运动方程式: dn. dE (1.42) w冒 px=F。s- 和 di 2 (1.43) 以及 E=器+k” 2 (1.44) 把笛卡尔坐标x推广到广义坐标9,相应的动量p:推广为广 义动量P,能量E推广为广义能量函数H(9,)。H(9,p)叫 做Hamilton函数。Hamilton函数可以看做是用坐标和共轭动 量表示的总能量(动能与势能之和).那么,对一维运动有一组 方程: 9= dH和书=-d只 (1.45) dq 称为Hamilton方程. 则对自由度为f的Hamilton运动方程为: aH 3p: (=1,2、…yf) (1.46) 卫:=- aH aq:
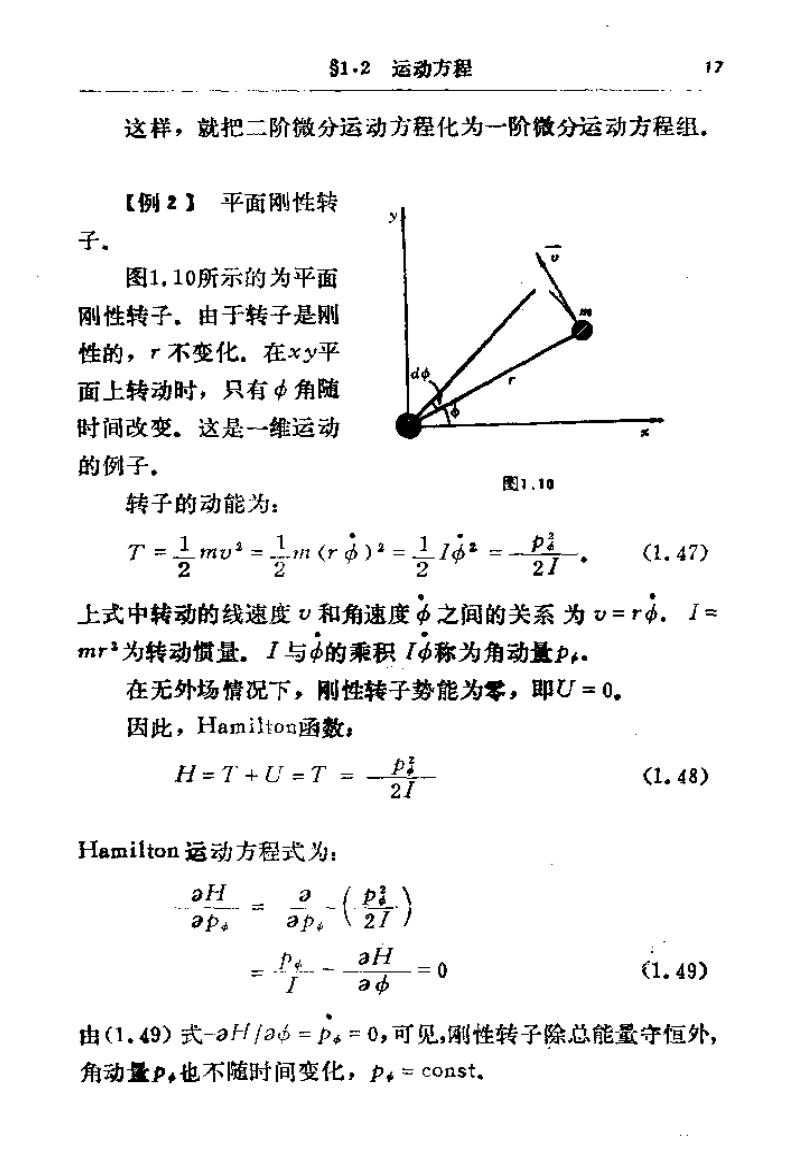
$1,2运动方程 17 这样,就把二阶微分运动方程化为一阶微分运动方程组. 【例2】平面刚性转 y 子 图1,10所示的为平面 刚性转子。由于转子是刚 性的,T不变化.在xy平 面上转动时,只有中角随 时间改变。这是一维运动 的例子。 图1.10 转子的动能为: (1.47) 2 上式中转动的线速度v和角速度中之间的关系为v=r.I= mr2为转动惯量。I与中的乘积I中称为角动量p 在无外场情况下,刚性转子势能为零,即U=0。 因此,Hamilton函数: H=T+U=T=-好 2 (1.48) Iamilton运动方程式为: ap。 品(》) aH -=0 ad 1.49) 由(1.49)式-aH/心=P。=0,可见,刚性转子除总能量守恒外, 角动量P,也不随时间变化,卫-co卫st

18 第一章相空间及Hamilton方程 刚性转予的相积分为: n.i.=∮p,d6=∫gdb =p,小d6=2p. (1.50) 因为平面刚性转子的角动 量D。是常数(M),则其 相积分P。I。=2xM是横 轴和纵坐标p。=M的直 线与纵轴和横坐标中=2π 的直线所围成的矩形面 2 积. 图1.12 ǐ例3】一维箱中的自由粒子。 ·个质量为m的粒子,作一维自由运动。假定粒子被限制 在长度为1的箱中,从而粒子的位置坐标必须在0运x≤1的 范围内、粒子在箱中不受力的作用。因此, 势能tJ=0. 动能7=号州正= (1.52) 27a .其amilton函数f1为: I1=1+U=p超 (1.52) 2m ~维箱中自由粒拉子的下amilton运动方程为: l=T.=.. ap。2p ,h p,=、 aH ax a=0 ax
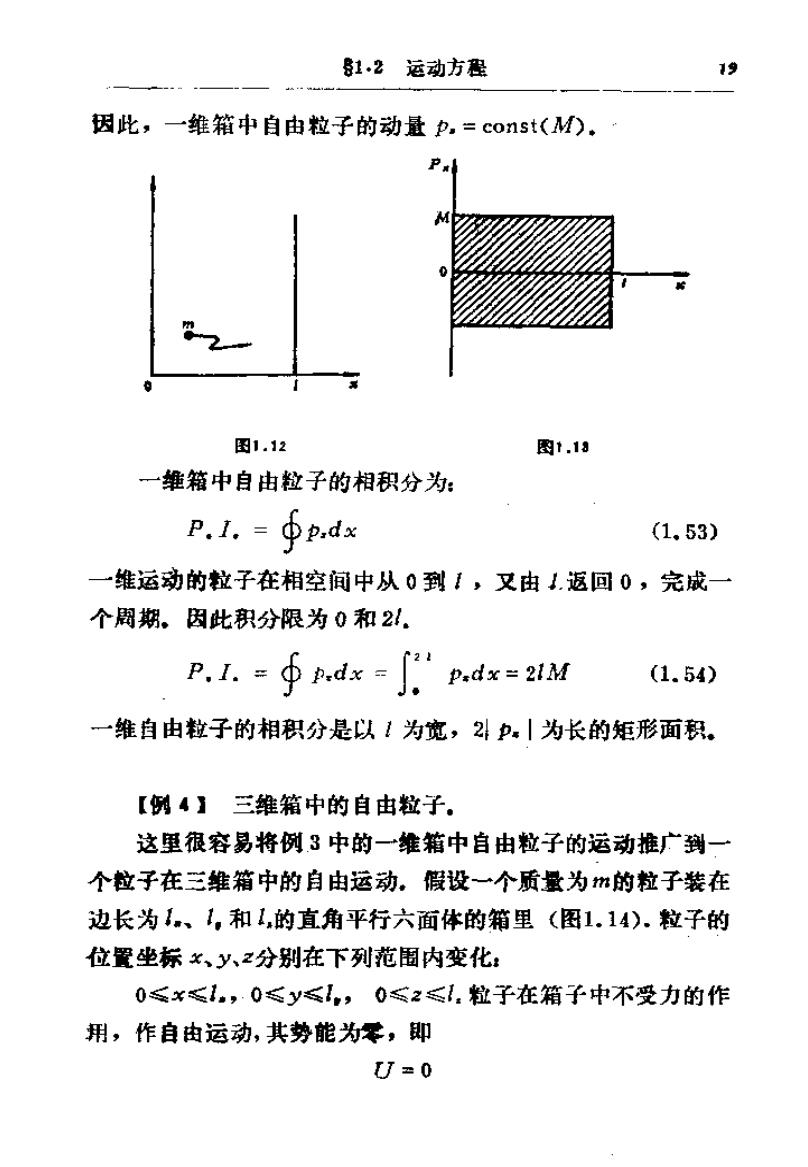
1.2运动方程 19 因此,一维箱中自由粒子的动量p,=const(M)。 图1.12 图1.1a 一维箱中自由粒子的相积分为: p.1.=∮p,dx (1.53) 一维运动的拉子在相空间中从0到1,又由1远回0,完成一 个周期。因此积分限为0和21. P,1.=∮dx=ig x=21M (1.54) 一维自由粒子的相积分是以1为宽,2p,|为长的矩形面积。 【例4】三维箱中的自由粒子。 这里很容易将例3中的一维箱中自由粒子的运动推广到一 个粒拉子在三维箱中的自由运动。假设一个质量为m的粒子装在 边长为1、1,和1,的直角平行六面体的箱里(图1.14).粒子的 位置坐标x、y、z分别在下列范围内变化: 0≤x≤1,0≤y≤I,0≤2≤l.粒子在箱子中不受力的作 用,作自由运动,其势能为零,即 U=0

20 第一草相空阀和Hami祖ton方程 其动能为: 2m 自由粒子的Hamilton阅 数为: H=E=T+U= p* 2 m (1.55) 因此,其动量为: 图1,14 p=√2m2 在三维箱巾作自由运动的粒子,有3个自由度,其相空间 是6维的相空间。在六维相空间中的体积元dTs为: drs=dxdydzdp dp,dp. (1.56) 某一能量E的等能面所包围的相体积就是对上式承积分: r。=Jdr=∫dxdydzdp.dh,dn, .dxf dy,dej∬dp.dp,dp. =Fj∬dp.d,dp. (1.57) 式中V=.1,l 对动量空间的积分,由图1.15可以看出: ∬dp.dp,dp.=4apd=亭xp (1.58) 因此,6维相空间的体积: r。=音xFp=号拉2mE)i (1.59) 这是分子相空间(:.空间)的体积: