
11体系状态的描述 11 相空闻是一个描述质点运动状态的空间。在相空间中,每 个点都代表着质点的一种运动状态,反之,质点的每一种运动 状态在相空间中都有一个代表点或相点.。当质点从一种运动状 态开始,经过一段时间后,变到另一种状态,则它在相空间中 就从一个相点移到另一个相点。在相空问中,连续移动的相点 可画出一条曲线,叫做相迹或相轨道,它就反映了质点的运动 规律。 对一个自由度为∫的分子,就需要2f维.相空间来描述其 运动状态。这种描写一个分子运动状态的相空间做4一空间, 也叫分子相空间。例如只有3.个平动自由度的质点,其相空间 就是2×3维的4空间。 由N个自由度为f的分子组成的体系,总自由度为Nf, 需要2fN维相空间来描述体系的运动状态,这种2fN维的相 空间叫做”=空间或气体空间。例如,每个质点自由度为3, 则需要6V维的T-空间来描述这N个质点组成的体系的运动软 态。T-空间中的一点,就代表W个质点在某瞬间的状态。 在4空间和”-空间中的体积元关系如下: 在“-空间中的体积元: 第1全分子为 (dxdydadp:dp,dp.)=dy 第2个分子为 (dxdydzdp.dpdp.)=dy: 第N个分子为 (dxdydzdp.dp,dp:)=dya 对N个分子组成的体系,在T-空间中其体积元为:
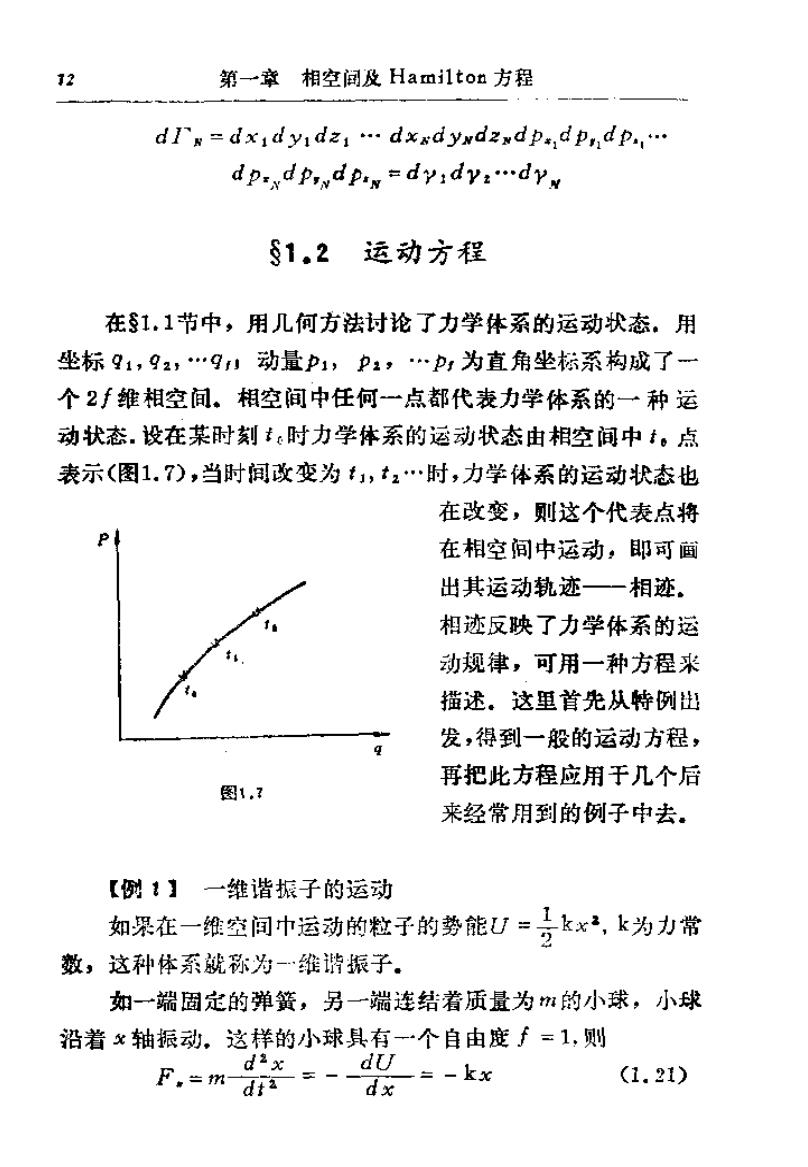
12 第一章相空闻及Hamilton方程 dIs=dx1dy1dz1…dxxdywdzxdp,dp,dp,… dpdpdp=dyidv:dy §1.2运动方程 在§1.1节中,用几何方法讨论了力学体系的运动状态。用 坐标91,92,…9」动量p1,p2,…p:为直角坐标系构城了一 个2f雏相空间。相空间中任何一点都代表力学体系的一种运 动状态.设在某时刻:时力学体系的运动状态由相空间中t。点 表示(图1.7),当时间改变为1,t2…时,力学体系的运动状态也 在改变,则这个代表点将 在相空间中运动,即可画 出其运动轨迹一一相迹。 相迹反映了力学体系的运 动规律,可用一种方程来 描述。这里首光从特例出 发,得到一般的运动方程, 再把此方程应用于几个后 图1. 来经常用到的例子中去. 【例】一维谐振子的运动 如哭在一维空间中运动的粒子的势能U=号k4,k为力常 数,这种体系就称为-…维谐振子. 如一端固定的弹簧,另一端连结着质量为m的小球,小球 沿着轴振动。这样的小球具有·个自由度f=1,则 P.m祭=-gka (1.21) dx

1,2运动方程 15 即小球所受的力F,和它 离开平衡位置(×=0)的 距离x成正比。“”号表 示受力和位移方向相反。 图1,s 解该微分方程,得 x三Acos(2rpt+a) (1.22) 式中A为振幅,y为频率,a为初相. x=-2Asin(2ayt+a) (1.23) x=-4πv24cos(2πyt+a) *-4π名y名X (1.24) 把(1.24)代入式mx=-kx中,得 ,/k (1.25) 式中上是常数,相当于虎克定律中的弹性常数。一维谐振子可 以模拟双原子分子中原子间振动、晶体中原子在晶格结点附近 的振动等。这些振动中,原子间引力的特性都反映在力常数上 中. 上面对一维谐振子运动的描述是经典力学中的Newton方 程,为二阶微分方程: F:=mx=m- dix dra (1.21) 在相空间中运用很不方便,不易求解。最好用一阶微分方程式 描述运动状态,故作如下变换。 -·维诺振子的总能量E是其动能T和势能U之和: E=T+U (1.26)

14 第一華相空间及Hamilton方程 对保守体系: E=T+U=const (1.27) 其中 (m) 2 (1.28) 2m p。=nx (1.29) p是动量的x方向分量. 势能J(x)只是坐标的函数: F.=m do,= = dp dt (1.30) F dx m dx dv,=mvdv. dt =dv:1dp: 2 2m (1.31) 或, (1.32) 对保守体系 =du dx dx (1.33) 因此 dp.=F.du dt dx (1.34) dU dx fdu-f kxdx (1.35) 因此总能量E为: E=+1kx 2m2 (1.36) 把k=4π2y*m代入(1.36)式: E=兰+2xy2mx 2 (1.37)

12运动方程 15 (1.37)式两边同除以E,即可得到一个椭圆方程式: x2 卫 (√E/2mrp2)2+(V2mE)=1 (1.38) 这是在xpx平面上的椭圆方程,其长半轴a=√E12mx2p, 短半轴b=V√2mE。可见在x和p.的二维相空间中,总能 量不变的曲线是一个椭圆。这是具有能量为E的谐振子的相点 在相空间中的相轨道(图1.9). 在相空间中,相迹围成的面 积叫做相积分P.I.(Phase Inte graI).相积分一般又称相体积, 即某一等能面所包围的相体积。 一维谐振子的相积分是一椭圆面 积: (1.39) 因为x=Aco3(2πy十a) 若初相a=0 图1. x=-2πvAsin(2xyt) p.=mx =-2mnvAsin(2nvt) P.1.p.diAmin(axvi)dt =2π*myA=-E (1.40) 在这种情祝下,振子的能量是: E=w…(P.I.) (1.41) 因此,在相空间中的体积元就与能量联系起来了