电路学习指导 第二章电阻电路的等效变换 第二章电阻电路的等效变换 一、基本要求 1.充分理解并掌握等效电路的概念。 2,熟练掌握电阻的分压公式和并联电阻的分流公式。 3.能熟练运用串联、并联等效电阻的公式对电阻混联电路进行化简 4.会运用电阻的三角形与星形联接相互变换的公式对电路进行化简。 5.熟练掌握对含源支路的等效变换。 6.能熟练掌握四种受控电源的电压电流关系,初步掌握含有受控电源的简单电路的计算。 二、本章要点 1.电路的等效变换 R3-. U U R R R (a) (b) 图2一1等效电阻电路 两个电路“等效”指他们对外电路的作用效果是相同的,即当电路中某一部分用其等 效电路代替后,未被代替部分的电压和电流均应保持不变。如图2一1所示电路中图(b) 称为图(a)的等效电路,即: U=U'1=' 2.电阻串并联电路 R1 Rz a Ist U U Rs (G.)(G2)G: b 图2一2电阻串联电路 图2一3电阻并联电路 (1)、电阻串联电路如图2一2所示, 11
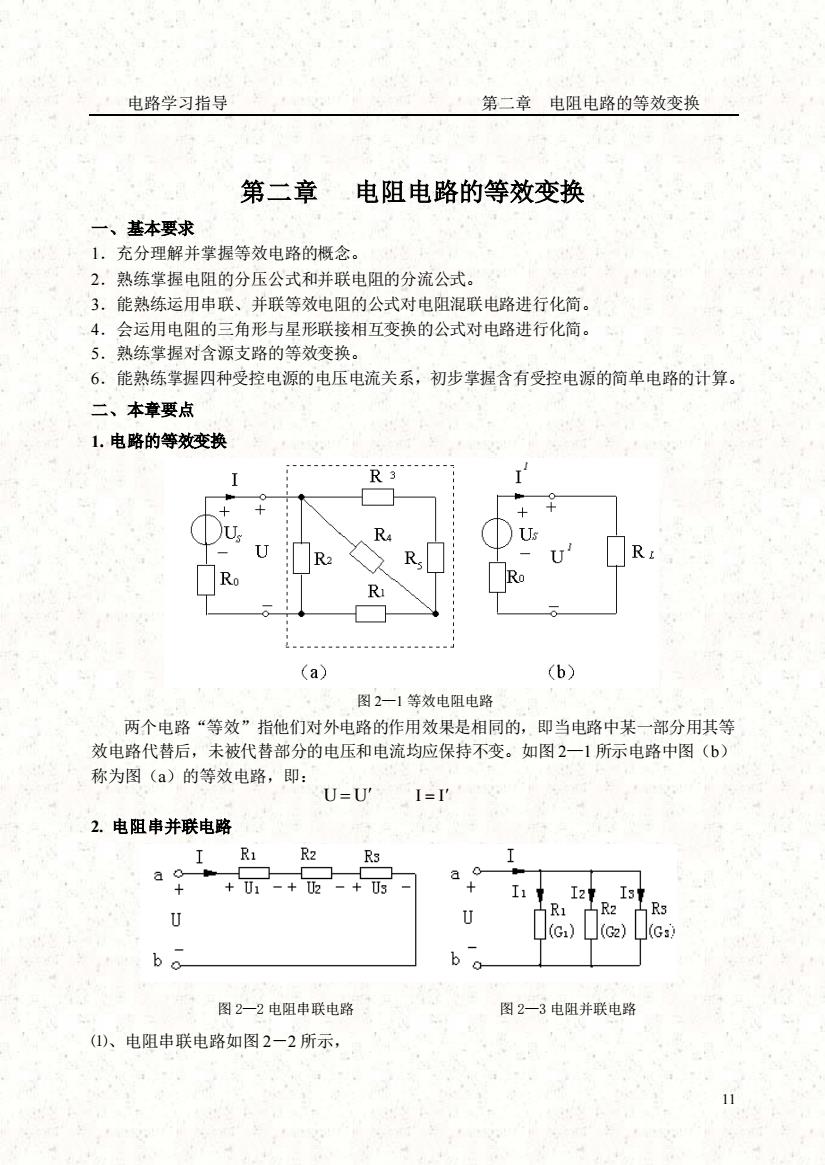
电路学习指导 第二章 电阻电路的等效变换 11 第二章 电阻电路的等效变换 一、基本要求 1.充分理解并掌握等效电路的概念。 2.熟练掌握电阻的分压公式和并联电阻的分流公式。 3.能熟练运用串联、并联等效电阻的公式对电阻混联电路进行化简。 4.会运用电阻的三角形与星形联接相互变换的公式对电路进行化简。 5.熟练掌握对含源支路的等效变换。 6.能熟练掌握四种受控电源的电压电流关系,初步掌握含有受控电源的简单电路的计算。 二、本章要点 1.电路的等效变换 图 2—1 等效电阻电路 两个电路“等效”指他们对外电路的作用效果是相同的,即当电路中某一部分用其等 效电路代替后,未被代替部分的电压和电流均应保持不变。如图 2—1 所示电路中图(b) 称为图(a)的等效电路,即: U = U I = I 2. 电阻串并联电路 图 2—2 电阻串联电路 图 2—3 电阻并联电路 ⑴、电阻串联电路如图 2-2 所示

电路学习指导 第二章电阻电路的等效变换 ①当n个电阻R、R.R串联时:串联等效电阻等于各电阻之和。 甲RR+R+R一含R ②分压公式为U:R。 Uk=1、2、n)即:各元件的电压与该元件的电阻值成正比 式中Rg为串联电路的等效电阻U为第k个电阻R上的电压,U为总电压 (②)、电阻并联电路如图2一3所示 当n个电阻R(或电导G)并联时: ①各电阻两端的电压是同一个电压。 ②并联等效电导等于各电阻元件电导之和。 即:G=G+G+G++G=2G ③分流公式为 =G1(为第k条支路G中的电流,I为 总电流)(k=1、2、3.) T ①当两个电阻并联时:等效电阻有R=R×R R+R2 分流公式可以写成为 图2一4两个电阻并联电路 3.如果能判断出电路的某一个支路中没有电流流过可以把这条支路拿掉,即作为开路:如果 能判断出电路中某两点的电位相等则可以把这两点短路。这在电路的分析、计算中常常是 很有用的。 4.电阻的星形(Y)和三角形(△)连接的等效变换。 (1)Y一△等效变换的公式: Y形电阻=△形相邻电阻的乘积 △形电阻之和 △形电阻=Y形电阻两两乘积之和 △形不相邻电阻之和 当三个电阻相等时,Ry=R。或R=3RY 5.含源支路的等效变换 ()当个理想电压源串联时,其可以用一个等效的理想电压源e米代替,且有 12
电路学习指导 第二章 电阻电路的等效变换 12 ①当 n 个电阻 R1 、R2.Rn 串联时:串联等效电阻等于各电阻之和。 即: Req=R1+R2+R3.Rn= = n k 1 Rk ② 分压公式为 U R R U eq k k = (k=1、2、.n) 即:各元件的电压与该元件的电阻值成正比. 式中 Req 为串联电路的等效电阻,Uk为第 k 个电阻 Rk 上的电压,U 为总电压 ⑵、电阻并联电路如图 2-3 所示 当 n 个电阻 R(或电导 G)并联时: ① 各电阻两端的电压是同一个电压。 ② 并联等效电导等于各电阻元件电导之和。 即:G=G1+G2+G3+.+Gn= = n k 1 Gk ③ 分流公式为 Ik= I G Gk (Ik为第 k 条支路 Gk中的电流,I 为 总电流)(k=1、2、3.n) ④ 当两个电阻并联时:等效电阻有 1 2 1 2 R R R R R + = 分流公式可以写成为 I R R R I 1 2 2 1 + = ; I R R R I 1 2 1 2 + = 图 2—4 两个电阻并联电路 3.如果能判断出电路的某一个支路中没有电流流过,可以把这条支路拿掉,即作为开路;如果 能判断出电路中某两点的电位相等,则可以把这两点短路。这在电路的分析、计算中常常是 很有用的。 4. 电阻的星形(Y)和三角形(△)连接的等效变换。 (1) Y-△等效变换的公式: 形电阻之和 形相邻电阻的乘积 形电阻 Y = 形不相邻电阻之和 形电阻两两乘积之和 形电阻 = 当三个电阻相等时, = R 3 1 R 或 R△=3RY 5.含源支路的等效变换 ⑴ 当 n 个理想电压源串联时,其可以用一个等效的理想电压源 es 来代替,且有

电路学习指导 第二章电阻电路的等效变换 6e1+eg+ter8e. (②)当个理想电流源并联时,其可以用一个等效的理想电流源1,来代替,且有 1=i+i如++in=2 (3)当若干个实际电压源串联时,可以简化成一个等效的电压源,其等效的电压源电压等于各 个电压源的电压的代数和,而其等效内阻等于各个电压源的内阻之和,且有 e-esl+eat+R++nR (④)当若干个实际电流源并联时,可以简化成一个等效的电流源,其等效的电流源电流等于 各个电流源的电流代数和,而其等效的内电导等于各个电流源的内导之和,且有 a+i++=a G-G:+G;++Gn-G (⑤)当若干个实际电流源串联时,应当先把它们变换成电压源,然后进行简化。 (⑥)当若干个实际电压源并联时,应当先把它们变换成电流源,然后进行简化。 (7)理想电压源和理想电流源不能进行等效变换 6.受控电源(非独立电源) 受控电源是一种非独立电源,其电压和电流与控制它的电压和电流成正比地变化。在 分析电路中,对受控原的处理与独立源并无原则区别,唯一要注意的是在对含有受控源的 电路进行化简时,必须要注意保留控制量所在的支路。 三、典型例题 1202 例2一1试求图2一5所示电路的等效电阻Rab 1209 解:从图可见,80Q两端被短接,即电阻值为零。 ao 120Q的三个电阻互相并联,然后与60Q的电阻串联, 120 80 故ab两端的等效电阻为: 609 R-60r写x120=100 b 例2一2试求图2一6所示电路的等效电阻Rab 图2-5例2-1图 解:从电路图可见是个平衡电桥,c,d两个点电位相等,可视为短路或开路。则 当cd短路时:Ra=(20/20)+60760F40Q 20 20 20g 20g 当cd开路时:Rab=(20+60)(20+60F40Q 可见:当cd等电位点的时候,将cd点开路或短路处 60/ 理对电路无任何影响。 0 e d 图2-6例2一2图
电路学习指导 第二章 电阻电路的等效变换 13 es=es1+es2+.+esn= = n k sk e 1 ⑵ 当 n 个理想电流源并联时,其可以用一个等效的理想电流源 is 来代替,且有 = = + + + = n k s s s sn sk i i i i i 1 1 2 ⑶ 当若干个实际电压源串联时,可以简化成一个等效的电压源,其等效的电压源电压等于各 个电压源的电压的代数和,而其等效内阻等于各个电压源的内阻之和,且有 es=es1+es2+.+esn= = n k 1 sk e ; R=R1+R2+.+Rn= = n k Rk 1 ⑷ 当若干个实际电流源并联时,可以简化成一个等效的电流源,其等效的电流源电流等于 各个电流源的电流代数和,而其等效的内电导等于各个电流源的内导之和,且有 = = + + + = n k s s s sn sk i i i i i 1 1 2 ; G=G1+G2+.+Gn= = n k Gk 1 ⑸ 当若干个实际电流源串联时,应当先把它们变换成电压源,然后进行简化。 ⑹ 当若干个实际电压源并联时,应当先把它们变换成电流源,然后进行简化。 (7)理想电压源和理想电流源不能进行等效变换 6.受控电源(非独立电源) 受控电源是一种非独立电源,其电压和电流与控制它的电压和电流成正比地变化。在 分析电路中,对受控原的处理与独立源并无原则区别,唯一要注意的是在对含有受控源的 电路进行化简时,必须要注意保留控制量所在的支路。 三、典型例题 例2-1 试求图 2—5 所示电路的等效电阻 Rab 解:从图可见,80Ω两端被短接,即电阻值为零。 120Ω的三个电阻互相并联,然后与 60Ω的电阻串联, 故 ab 两端的等效电阻为: Rab=60+ 120 3 1 =100Ω 例 2-2 试求图 2—6 所示电路的等效电阻 Rab 图 2—5 例 2—1 图 解:从电路图可见是个平衡电桥,c,d 两个点电位相等,可视为短路或开路。则 当 cd 短路时: Rab=(20//20)+(60//60)= 40Ω 当 cd 开路时: Rab=(20+60)//(20+60)= 40Ω 可见:当 cd 等电位点的时候,将 cd 点开路或短路处 理对电路无任何影响。 图 2—6 例 2—2 图

电路学习指导 第二章电阻电路的等效变换 例2-3试求图2-7所示电路的等效电阻Rab。 102 209 八20 102 109 102 609 (a) (b) 图2-7例2-3图 解:先把10Q的三个电阻进行Y-△等效变换,作出图2-6(a)的等效电路如图2 -6(b)所示,其中的30Q电阻是由Y-△等效变换而来的,即: R=3R¥=3×10-30Q 再计算Rab:Rab(10/30)MW[(20/30)+(30M60)]=6.075Q Rab=6.075Q 例2一4如图2-8(a)电路中,R1=R=R=R=30Q,试求下列三种情况下a、b两点 之间的等效电阻Rb:(1)S1和S闭合,其它断开:(2)S、S3和S5闭合,其它断开: (3)S1.、S3和S4闭合,其它断开。 R:R2 2-8例2-4
电路学习指导 第二章 电阻电路的等效变换 14 例 2-3 试求图 2—7 所示电路的等效电阻 Rab。 (a) (b) 图 2—7 例 2—3 图 解:先把 10Ω的三个电阻进行 Y-Δ等效变换,作出图 2-6(a)的等效电路如图 2 -6(b)所示,其中的 30Ω电阻是由 Y-Δ等效变换而来的,即: RΔ=3RY=3×10=30Ω 再计算 Rab:Rab=(10//30)//[(20//30)+(30//60)]=6.075Ω Rab=6.075Ω 例 2-4 如图 2-8(a)电路中,R1=R2=R3=R4=30Ω,试求下列三种情况下 a、b 两点 之间的等效电阻 Rab:(1)S1 和 S5 闭合,其它断开;(2)S2 、S3 和 S5 闭合,其它断开; (3)S1、S3 和 S4 闭合,其它断开。 图 2-8 例 2-4 图

电路学习指导 第二章电阻电路的等效变换 解:根据开关打开和闭合情况,适当改画电路进行分析。 (1)根据题意,当S1、Ss闭合时,电路图可改画成如图2一8(b)所示,可见R4被 短接,等效电阻Rab为: Rab=R1+R+R3=30+30+30=902 (2)当S2、S.、S闭合时,电路图可改画成如图2一6(c)所示,这相当于R、R、 R三个电阻并联,所以等效电阻Rab为: Rab-R+(R/R∥R)=30+×30=400 (3)当S1、S.、S4闭合时,电路图可改画成如图2-8()所示,此时R2、R3电阻 被短接,R和R并联,等效电阻Rab为: Rab-R1∥R=别9-15a 例2一5求图2-9所示电路的等效电路。 解:等效化简中将与电压源并联的电阻元件拆除,电流源支路中串联的电阻元件置 零。如图(b)所示,其余化简如图(c、(d)、(e)所示 (6) 5a (d) (e) 图2-9例2-5图 例2一6求图2-10所示电路的等效电路。 解:在图()电路中,根据电流源特性,3A电流源与6V电压源的串联等效为一个3A的电 流源如图b)所示,然后3A与2A的电流源合并为一个5A的电流源而5A的电流源与8 的电压源的串联等效为一个5A的电流源如图©)所示
电路学习指导 第二章 电阻电路的等效变换 15 解: 根据开关打开和闭合情况,适当改画电路进行分析。 (1)根据题意,当S1、S5 闭合时,电路图可改画成如图 2-8(b)所示,可见 R4 被 短接,等效电阻 Rab 为: Rab=R1+R2+R3=30+30+30=90Ω (2)当 S2、S3、S5闭合时,电路图可改画成如图 2-6(c)所示,这相当于 R2、R3、 R4 三个电阻并联,所以等效电阻 Rab 为: Rab=R1+(R2 ∥R3 ∥R4)=30+ 30 3 1 = 40Ω (3)当 S1、S3、S4 闭合时,电路图可改画成如图 2-8(d)所示,此时 R2、R3 电阻 被短接,R1 和 R4 并联,等效电阻 Rab 为: Rab= R1∥R4= 30 30 30 30 + =15Ω 例 2-5 求图 2-9 所示电路的等效电路。 解: 等效化简中将与电压源并联的电阻元件拆除,电流源支路中串联的电阻元件置 零。如图(b)所示,其余化简如图(c)、(d)、(e)所示 + - 10V 2Ω 6Ω 2A 3Ω - + 4V a b - 2Ω 2A b + 10V - 4V + a 2Ω 2A b - 4V + a 5A 14V 2Ω - b + - + 4V a + 2Ω - b 18V a (a) (b) (c) (d) (e) 图 2-9 例 2-5 图 例 2-6 求图 2-10 所示电路的等效电路。 解:在图(a)电路中,根据电流源特性,3A 电流源与 6V 电压源的串联等效为一个 3A 的电 流源如图(b)所示, 然后 3A 与 2A 的电流源合并为一个 5A 的电流源,而 5A 的电流源与 8V 的电压源的串联等效为一个 5A 的电流源如图(c)所示