
电路学习指导 第九章含有耦合电感的电路 第九章含有耦合电感的电路 一.基本要求 1.掌握互感线圈中电压、电流的关系,了解互感系数、同名端的含义。 2.会应用互感消去法(去耦法)分析计算含有互感的电路,这是本章的重点。 3.熟悉空心变压器的原、副边等效电路。 4.熟悉理想变压器的三个作用:变换电压、电流、阻抗。 二本章要点 1.两互感的伏安关系(耦合电感又称互感) 4=L±M 或0=joLd±joMis, lU2=joLi2±joMi dt 电压、电流取关联参考方向时,同名端为同侧时,互感电压取“+”号,同名端为异侧时, 互感电压取“-”号。 2.同名端 同名端又称对应端,电流分别从同名端流入时,所产生的互感磁通与自感磁通的方向一致 (互相增强)。 3.含互感电路的分析方法 1>可将互感电压用一个电流控制电压源(CCVS)替代,然后用一般分析方法进行分析计算 2>互感消去法(去耦法) <1>互感串联 两互感串联的等效电感为: L=山+山±2M顺接时取“4”号,。兴。 反接时取“一”号。 图9-1两互感串联电路 <2>一般情况(具有公共节点) 2 2 0 03) 图9-2互感消去等效电路 75
电路学习指导 第九章 含有耦合电感的电路 75 第九章 含有耦合电感的电路 一. 基本要求 1.掌握互感线圈中电压、电流的关系,了解互感系数、同名端的含义。 2.会应用互感消去法(去耦法)分析计算含有互感的电路,这是本章的重点。 3.熟悉空心变压器的原、副边等效电路。 4.熟悉理想变压器的三个作用:变换电压、电流、阻抗。 二.本章要点 1.两互感的伏安关系(耦合电感又称互感) = = dt di M dt di u L dt di M dt di u L 2 1 2 2 1 2 1 1 或 = = 2 2 2 1 1 1 1 2 j j j j U L I MI U L I MI 电压、电流取关联参考方向时,同名端为同侧时,互感电压取“+”号,同名端为异侧时, 互感电压取“-”号。 2.同名端 同名端又称对应端,电流分别从同名端流入时,所产生的互感磁通与自感磁通的方向一致 (互相增强)。 3.含互感电路的分析方法 1>可将互感电压用一个电流控制电压源(CCVS)替代,然后用一般分析方法进行分析计算。 2>互感消去法(去耦法) <1>互感串联 两互感串联的等效电感为: L = L1 + L2 2M 顺接时取“+”号, 反接时取“-”号。 图 9-1 两互感串联电路 <2>一般情况(具有公共节点) 图 9-2 互感消去等效电路

电路学习指导 第九章含有耦合电感的电路 4.空心变压器 ①0 Z22 ④①ioc Z22 a)原边等效电路 b)副边等效电路 图9-3 空心变压器等效电路 原边:1= U 乙,=丝为引入阻抗。 -Uo ,心c=兰心开路电压:乙=丝等效阻抗。 Zu Z 5.理想变压器 1 n1 图9-4 理想变压器电路 1)变电压: =n,0=n心,2》变电流:4 0=n2Z 3》变阻抗:Z= 6.耦合系数K 耦合系数K定量描述了两个耦合线圈耦合的紧密程度,K的大小与线圈的结构,两线 圈的相互位置及周围磁介质有关,耦合系数为K= M -s1。 L 三,典型例愿 例9-1图示电路已知R=R=1502,L4=3H,L2=10H,M=4.5H, 0=220∠0V,o=100md/s,求电流i及两线圈端电压0,02。 解:串联反接Z=(R+R2)+j0L+L2-2M0=(300+j400)2=500∠53.132
电路学习指导 第九章 含有耦合电感的电路 76 4.空心变压器 a)原边等效电路 b)副边等效电路 图 9-3 空心变压器等效电路 原边: Z Z r U I 11 1 1 1 + = 22 2 M 1 Z X Z r = 为引入阻抗, 副边: eq 22 OC 2 Z Z U I + − = , 1 11 M OC U Z Z U = 开路电压; 11 2 M eq Z X Z = 等效阻抗。 5.理想变压器 a) b) 图 9-4 理想变压器电路 1) 变电压: n U U = 2 1 ,U1 nU2 = 2) 变电流: I n I 1 2 1 = − , 1 2 1 I n I = − 3) 变阻抗: n Z I U Z 2 1 1 in = = 6.耦合系数 K 耦合系数 K 定量描述了两个耦合线圈耦合的紧密程度, K 的大小与线圈的结构,两线 圈的相互位置及周围磁介质有关,耦合系数为 1 1 2 = L L M K 。 三.典型例题 例 9-1 图 示 电 路 已 知 R1 = R2 =150 , L1 = 3H , L2 =10H , M = 4.5H , U = 2200V, =100rad /s ,求电流 I 及两线圈端电压 U1 ,U2 。 解:串联反接 Z = (R1 + R2 ) + j(L1 + L2 − 2M ) = (300 + j400) = 50053.13

电路学习指导 第九章含有耦合电感的电路 .i= .220∠0° Z300∠53.130=04∠-53.13A 两线圈端电压分别为 。色k U=(R+j@L-j@M)i h 02 =(150+j300-j450)×0.44∠-53.13° =93.3∠-98.1V Uz=(R+joL-joM)i 图9-5例题9-1图 =(150+j1000-j450)×0.44∠-53.13°=250.8∠21.65V 例9-2工频交流电源电压U=220V,两互感线圈串联,顺接时,电流为3A,功率 为225W,反接时电流为8A。求两线圈的互感M。 解:顺接时Z=(R+R2)+jO(L1+L2+2M) 反接时Z'=(R+R)+jo(L4+L2-2M) 顺接时:4-2”-7乃30 3 (L+l2+2M0=☑-R2=6894n 4+h+2M-684-022H0 314 反接时:Z1=20=2750 o(4+b2-2M0=-R2=1.462 L4+-2M=146=0.0365H② 314 互感M:M=4+。+20=4+L-2M_02-00365-00459H 4 4 例9-3图示电路,R=32,R2=52,oL=7.52,oL2=12.50,oM=62, U=50∠0V,分别求开关S打开和闭合时的电流。 解:1)S打开,两线圈为串联顺接 Z=(R+R2)+jo(L1+L2+2M0=(8+j32)2 Z8+3及=152∠-75.96A n
电路学习指导 第九章 含有耦合电感的电路 77 ∴ 0.44 53.13 A 500 53.13 220 0 = − = = Z U I 两线圈端电压分别为 U R L M I 1 = ( 1 + j 1 − j ) = (150 + j300 − j450)0.44−53.13 = 93.3 − 98.1V U R L M I 2 = ( 2 + j 2 − j ) 图 9-5 例题 9-1 图 = (150 + j1000 − j450)0.44−53.13 = 250.821.65V 例 9-2 工频交流电源电压 U = 220V ,两互感线圈串联,顺接时,电流为 3A ,功率 为 225W ,反接时电流为 8A 。求两线圈的互感 M 。 解:顺接时 Z = (R1 + R2 ) + j(L1 + L2 + 2M ) 反接时 Z = (R1 + R2 ) + j(L1 + L2 − 2M ) 顺接时: = = 73.33 3 220 Z P I R 2 = ,∴ = + = = = 25 3 225 2 2 1 2 I P R R R ( + + 2 ) = − = 68.94 2 2 L1 L2 M Z R 0.22H 314 68.94 L1 + L2 + 2M = = ① 反接时: = = 27.5 8 220 Z ( + − 2 ) = − =11.46 2 2 L1 L2 M Z R 0.0365H 314 11.46 L1 + L2 − 2M = = ② 互感 M : 0.0459H 4 0.22 0.0365 4 ( 1 2 2 ) ( 1 2 2 ) = − = + + − + − = L L M L L M M 例 9-3 图示电路, R1 = 3, R2 = 5 ,L1 = 7.5 ,L2 =12.5 ,M = 6 , U = 500V ,分别求开关 S 打开和闭合时的电流 I 。 解:1) S 打开,两线圈为串联顺接 Z = (R1 + R2 ) + j(L1 + L2 + 2M ) = (8 + j32) 1.52 75.96 A 8 32 50 0 = − + = = Z j U I
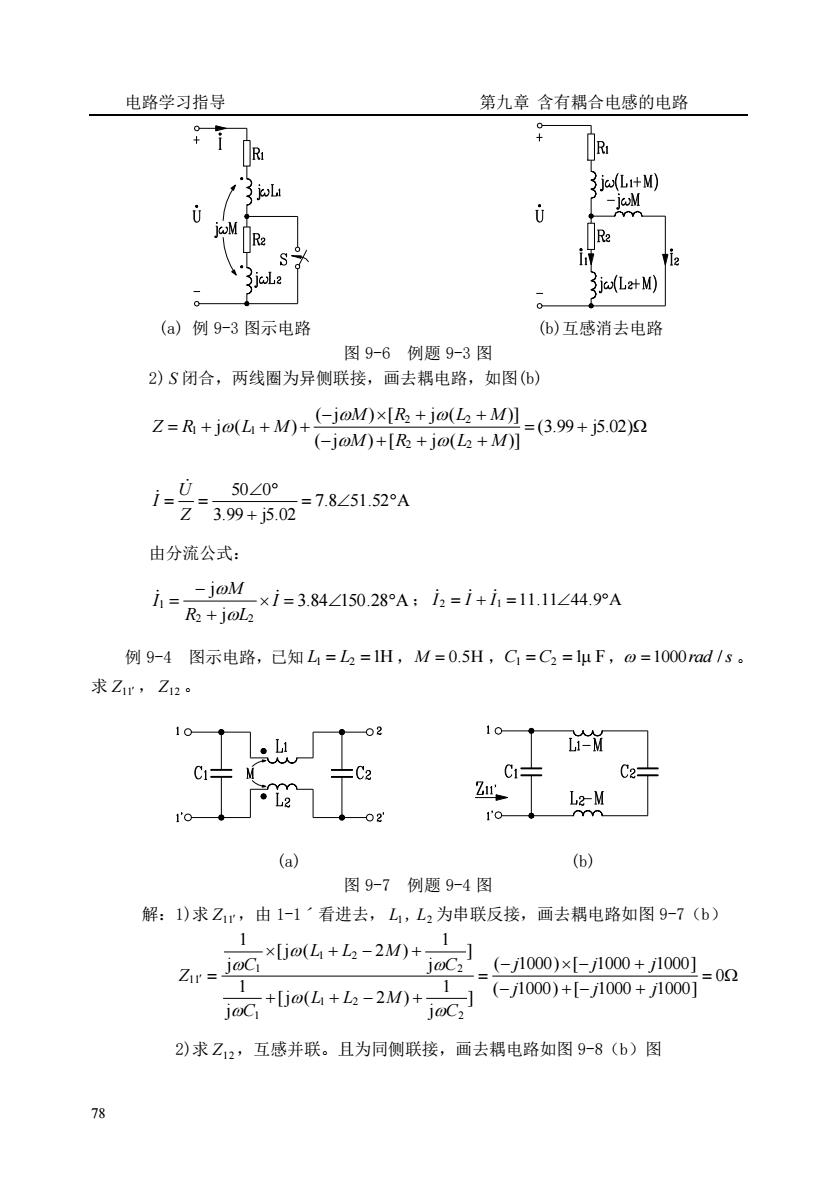
电路学习指导 第九章含有耦合电感的电路 R 8 jco(L+M) 2 3j(L2+M) (a)例9-3图示电路 (6)互感消去电路 图9-6例题9-3图 2)S闭合,两线圈为异侧联接,画去耦电路,如图(6) Z=R+j()+jMj()=(39+j5.02) (-joM)+[R+jo(L2+M)] 50∠0° FZ-39+50278∠51.52A 由分流公式: i=- -joM×i=3.84∠5028A:h=i+i=111∠4,9A 例9-4图示电路,已知L=L2=H,M=0.5H,C=C2=μF,o=1000md1s。 求Zr,Z12。 10 M C C2- 02 Le-M (a) (b) 图9-7例题9-4图 解:1)求Z,由1-1看进去,L1,L2为串联反接,画去耦电路如图9-7(b) Zr=Go4+6-2m joC2_(-1000)×-1000+j1000] =02 Go4+b-20+6G]0+00+7n0 2)求Z2,互感并联。且为同侧联接,画去耦电路如图9-8(b)图
电路学习指导 第九章 含有耦合电感的电路 78 (a) 例 9-3 图示电路 (b)互感消去电路 图 9-6 例题 9-3 图 2) S 闭合,两线圈为异侧联接,画去耦电路,如图(b) = + − + + + − + + = + + + (3.99 j5.02) ( j ) [ j ( )] ( j ) [ j ( )] j ( ) 2 2 2 2 1 1 M R L M M R L M Z R L M 7.8 51.52 A 3.99 j5.02 50 0 = + = = Z U I 由分流公式: 3.84 150.28 A j j 2 2 1 = + − = I R L M I ; I 2 = I + I 1 =11.1144.9A 例 9-4 图示电路,已知 L1 = L2 =1H ,M = 0.5H ,C1 =C2 =1μ F, =1000rad /s 。 求 Z11 , Z12 。 (a) (b) 图 9-7 例题 9-4 图 解:1)求 Z11 ,由 1-1ˊ看进去, L1 , L2 为串联反接,画去耦电路如图 9-7(b) = − + − + − − + = + + − + + − + = 0 ( 1000) [ 1000 1000] ( 1000) [ 1000 1000] ] j 1 [j ( 2 ) j 1 ] j 1 [j ( 2 ) j 1 2 1 2 1 2 1 2 1 11 j j j j j j C L L M C C L L M C Z 2)求 Z12 ,互感并联。且为同侧联接,画去耦电路如图 9-8(b)图
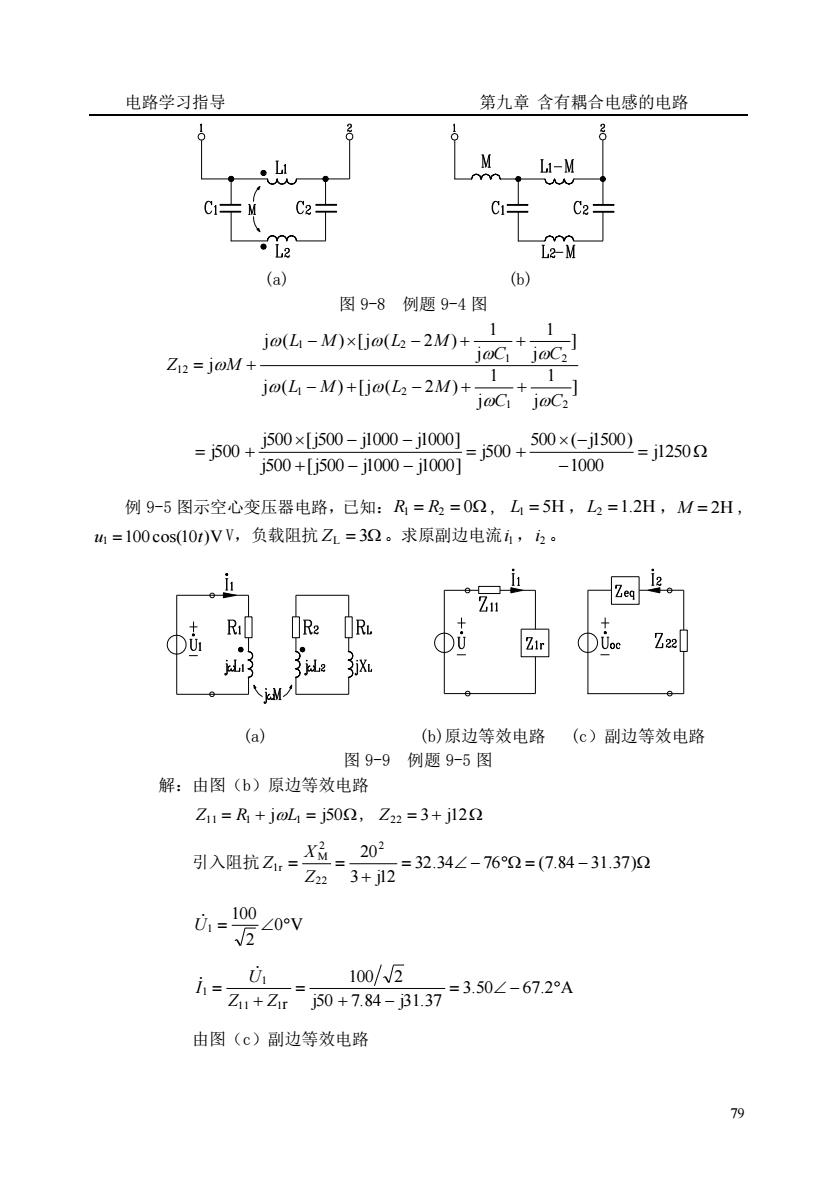
电路学习指导 第九章含有耦合电感的电路 8 M C÷C2 (a) (6) 图9-8例题9-4图 1 Zn2 =joM+ j()xi(M)+jacj 1 j@(L-M)+[j@(Lz-2M)+- ncjnc] -j50+i500×[5s00-j100-j1001-j500+50x150)-j1250n j500+[j500-j1000-j1000] -1000 例9-5图示空心变压器电路,已知:R=R=02,L1=5H,L2=1.2H,M=2H h=100cos(10)VV,负载阻抗Z1=32。求原副边电流i,2。 Zu Z22 13 八M儿 6 (6)原边等效电路 (c)副边等效电路 图9-9例题9-5图 解:由图(b)原边等效电路 Z1=R+joL1=j502,Z22=3+j122 引队抗2.装-2=23-6n0-1370 Z22 d,-100∠0v 100/W5 1=Z+50+174-17350<-672A 由图(c)副边等效电路 79
电路学习指导 第九章 含有耦合电感的电路 79 (a) (b) 图 9-8 例题 9-4 图 ] j 1 j 1 j ( ) [j ( 2 ) ] j 1 j 1 j ( ) [j ( 2 ) j 1 2 1 2 1 2 1 2 12 C C L M L M C C L M L M Z M − + − + + − − + + = + = − − = + + − − − − = + j1250 1000 500 ( j1500) j500 j500 [j500 j1000 j1000] j500 [j500 j1000 j1000] j500 例 9-5 图示空心变压器电路,已知: R1 = R2 = 0 , L1 = 5H ,L2 =1.2H ,M = 2H , u1 =100 cos(10t)V V,负载阻抗 ZL = 3 。求原副边电流 i1 ,i2 。 (a) (b)原边等效电路 (c)副边等效电路 图 9-9 例题 9-5 图 解:由图(b)原边等效电路 Z11 = R1 + jL1 = j50, Z22 = 3 + j12 引入阻抗 = − = − + = = 32.34 76 (7.84 31.37) 3 j12 202 22 2 M 1r Z X Z 0 V 2 100 U1 = 3.50 67.2 A j50 7.84 j31.37 100 2 11 1r 1 1 = − + − = + = Z Z U I 由图(c)副边等效电路