
平面及其方程 曲面方程与空间曲线方程概念 二、 平面的点法式方程 三、平面的一般方程 四、 两平面的夹角
平面及其方程 一、曲面方程与空间曲线方程概念 二、平面的点法式方程 三、平面的一般方程 四、两平面的夹角

>方程的建立 通过点M(xo,yo,o) 设平面· 垂直于非零向量=(A,B,C),一法向量 任取M(x,y,z)eΠ, →MoM1月 →MM·n=0 MoM=(x-x0,y-y0,2=20) A(x-xo)+B(y-y%)+C(2-0)=0 平面Π的点法式方程
z y x o M0 n ( , , ) 0 0 0 0 通过点 M x y z 垂直于非零向量 ( ) ( ) ( ) 0 A x − x0 + B y − y0 + C z − z0 = M 平面的点法式方程 设平面 M ( x, y,z) , n = (A , B, C), M M ⊥n 0 0 M0M n = 任取 ➢方程的建立 法向量
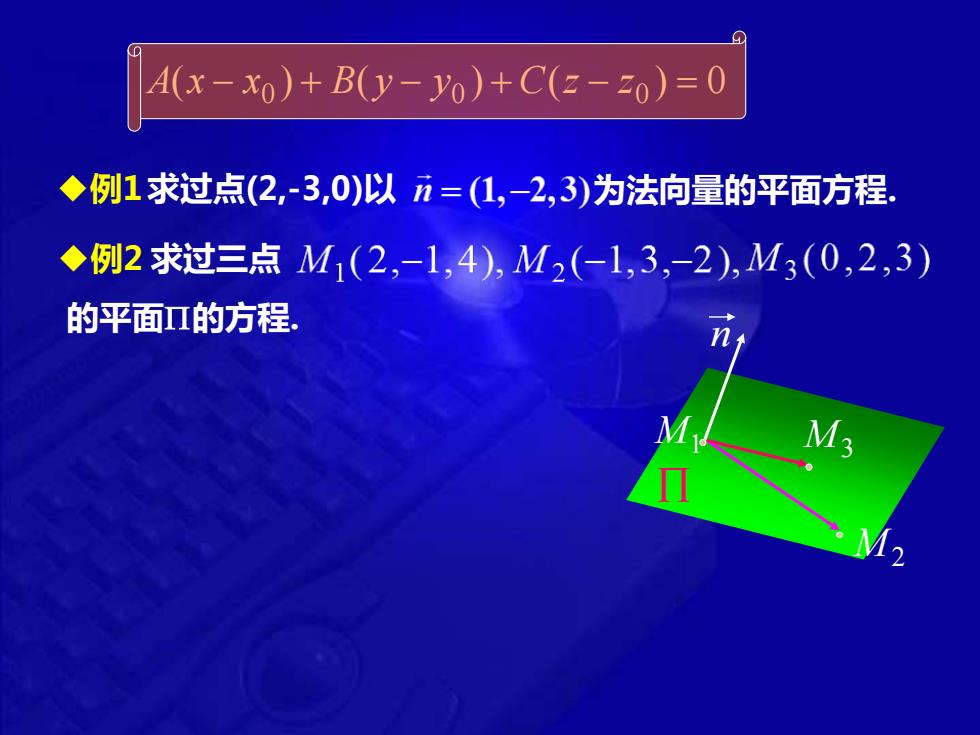
A(x-x0)+B(y-y0)+C(2-20)=0 ◆例1求过点(2,-3,0)以=(1,-2,3)为法向量的平面方程 ◆例2求过三点M1(2,-1,4),M2(-1,3,-2),M3(0,2,3) 的平面Π的方程, M3
M1 M2 M3 求过三点 的平面的方程. n ◆例2 ( ) ( ) ( ) 0 A x − x0 + B y − y0 + C z − z0 = ◆例1求过点(2,-3,0)以 为法向量的平面方程
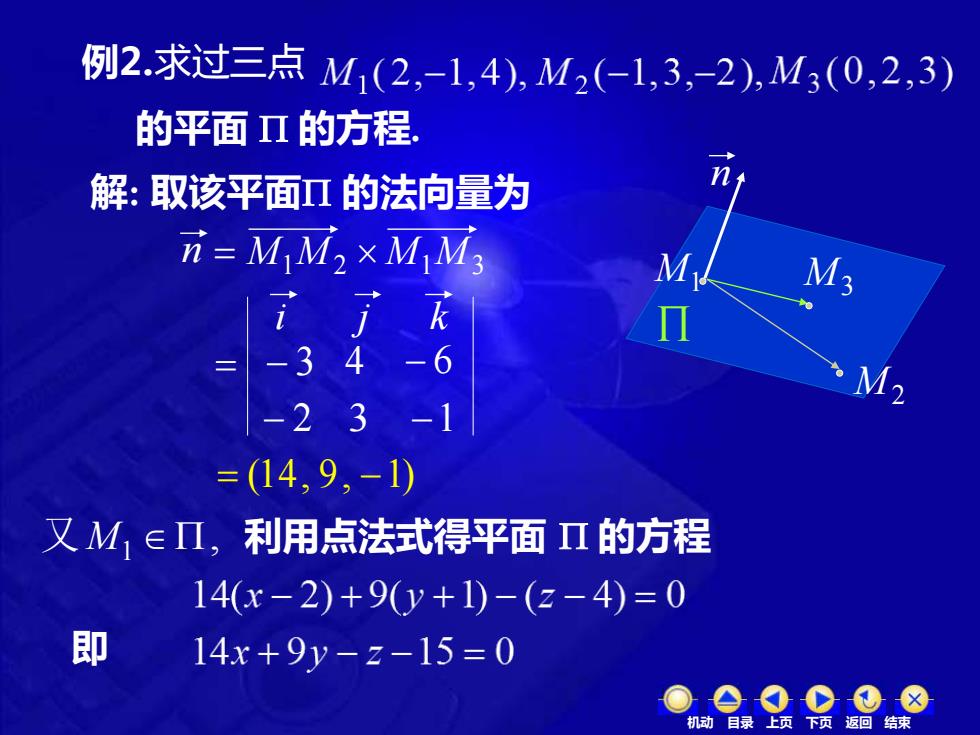
例2.求过三点M1(2,-1,4),M2(-1,3,-2),M3(0,2,3) 的平面Π的方程 解:取该平面Π的法向量为 n=MM2×MM3 M M3 Π -34-6 M2 -23-1 =(14,9,-1) 又M,∈·,利用点法式得平面Ⅱ的方程 14(x-2)+9y+1)-(2-4)=0 即 14x+9y-z-15=0 机动目录上页下页返回结束
i j k = 例2.求过三点 , 又M1 = (14, 9, −1) 即 M1 M2 M3 解: 取该平面 的法向量为 的平面 的方程. 利用点法式得平面 的方程 − 3 4 − 6 − 2 3 −1 n n = M1M 2 M1M3 机动 目录 上页 下页 返回 结束