2.3回路法和网孔法 二、特殊情况的处理 2、受控源的处理方法 例:用回路法求电压u。 0.1w 解:对回路1和3 i1=0.1w, 3=4 61 12V 对回路2 221 -2i1+26i2-20i3=12 上述一些方程中会出现受控源的控制变量u, 202 用回路电流表示该控制变量,有 92 40 u=20(i3-i2) 解得i2=3.6(A),u=8(V)。 小结★:对受控源首先将它看成独立电源;列方程后,再补一个方 程将控制量用回路电流表示。 11
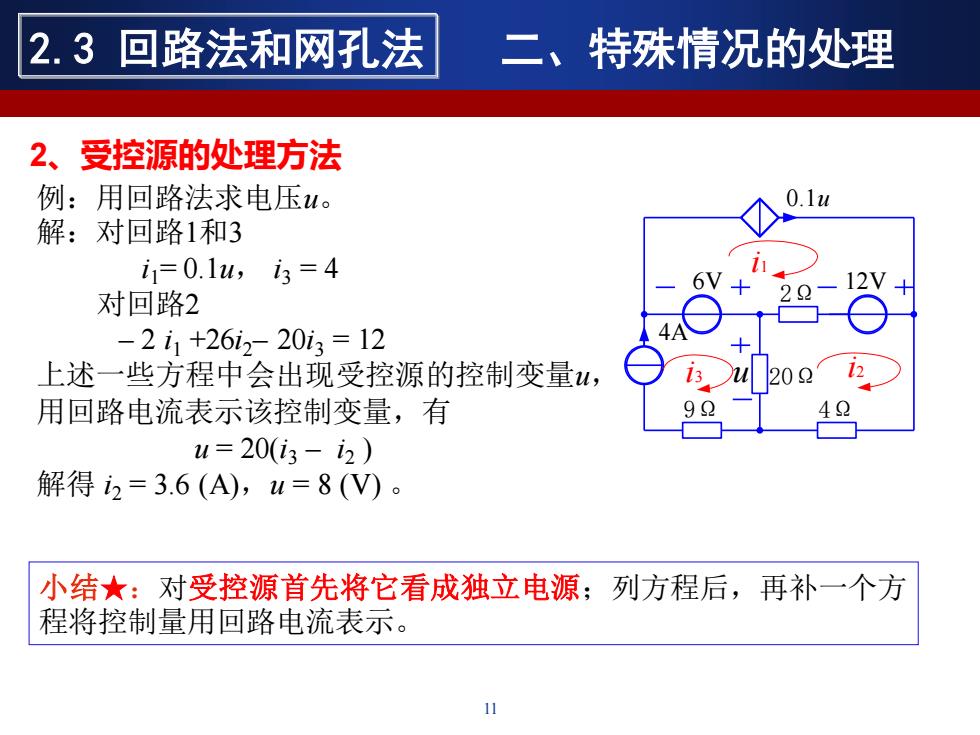
11 例:用回路法求电压u。 u 20Ω i1 0.1u i2 i3 2Ω 9Ω 4Ω 6V 12V 4A 解:对回路1和3 i1= 0.1u, i3 = 4 对回路2 – 2 i1 +26i2– 20i3 = 12 上述一些方程中会出现受控源的控制变量u, 用回路电流表示该控制变量,有 u = 20(i3 – i2 ) 解得 i2 = 3.6 (A),u = 8 (V) 。 小结★:对受控源首先将它看成独立电源;列方程后,再补一个方 程将控制量用回路电流表示。 2、受控源的处理方法 2.3 回路法和网孔法 二、特殊情况的处理
2.3回路法和网孔法 二、特殊情况的处理 2、受控源的处理方法 6 2 思考: 1.若受控电流源与20欧电阻互换位置,如何处理? (1)将受控电流源当成电流源,设电压,补“回路电流-电流源电 流”方程和“回路电流-受控变量”方程 (2)巧妙取独立回路! 2.若受控电流源变为受控电压源呢? 更简单!当成独立电压源,补“回路电流受控变量”方程即可
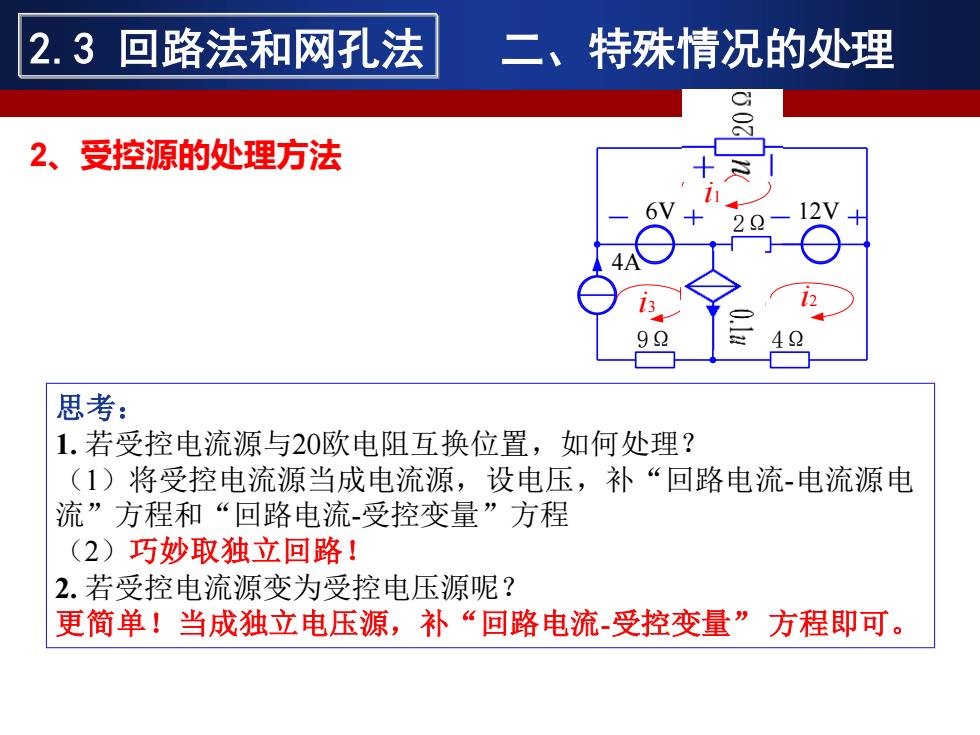
u 20Ω i1 0.1u i2 i3 2Ω 9Ω 4Ω 6V 12V 4A 思考: 1. 若受控电流源与20欧电阻互换位置,如何处理? (1)将受控电流源当成电流源,设电压,补“回路电流-电流源电 流”方程和“回路电流-受控变量”方程 (2)巧妙取独立回路! 2. 若受控电流源变为受控电压源呢? 更简单!当成独立电压源,补“回路电流-受控变量” 方程即可。 2、受控源的处理方法 2.3 回路法和网孔法 二、特殊情况的处理

2.4 节点法 一、节点法大 1、节点法:以节点电压为电路变量,并对独立节点用KCL列出用节 点电压表达有关支路电流的方程的求解方法。 列写方程个数:n-1 2、节点电压 在电路中任意选择一个节点为参考节点,其余节点与参考节点 之间的电压,称为节点电压或节点电位,各节点电压的极性均以 参考节点为“”极
2.4 节点法 13 2、节点电压 在电路中任意选择一个节点为参考节点,其余节点与参考节点 之间的电压,称为节点电压或节点电位,各节点电压的极性均以 参考节点为“-”极。 1、节点法:以节点电压为电路变量,并对独立节点用KCL列出用节 点电压表达有关支路电流的方程的求解方法。 一、节点法★ 列写方程个数:n - 1
2.4节点法 一、节点法 G1 如图电路,选节点4作参考点,其余各节 点的电压分别记为u1、2和3 G2 G3 支路电压可用节点电压表示为: u12=u1-W2,u23=u2-W3,u13=u1-3 ,u14=u1,u24=u2,u34=3. 对电路的任意回路,如回路A,有 u13-l23-U12 =41-43-(u2-u3)-(u1-w2)=0 节点电压的独立性 节点电压自动满足KVL方程。 和完备性。 14
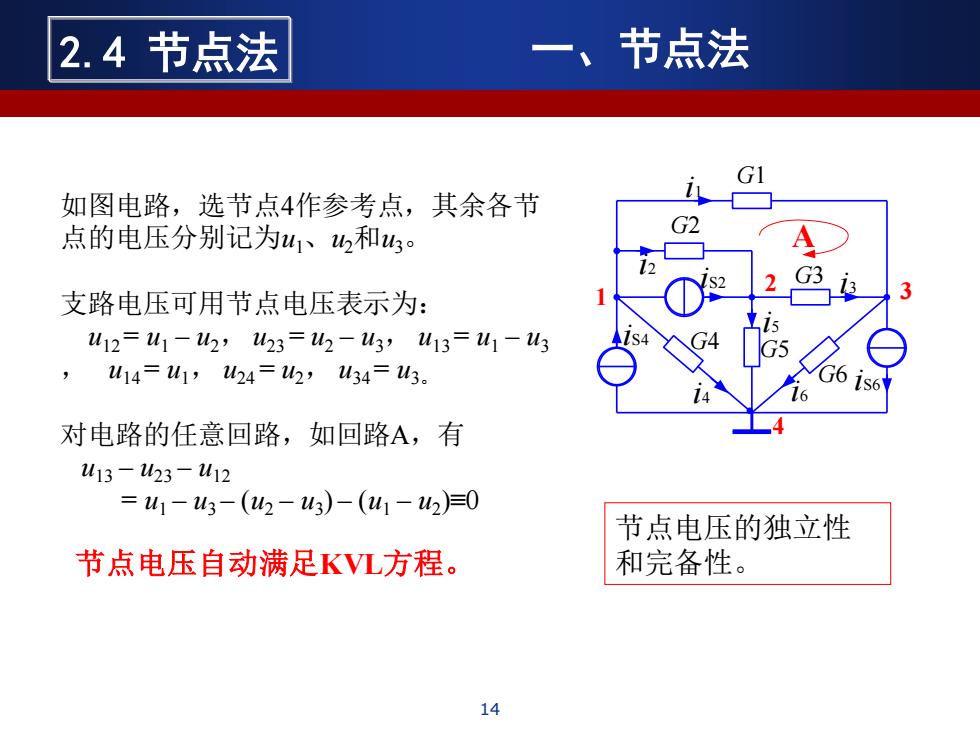
14 2.4 节点法 一、节点法 i4 G1 G2 G4 G6 1 i2 iS2 i5 A G3 G5 iS4 iS6 2 3 4 i1 i3 i6 如图电路,选节点4作参考点,其余各节 点的电压分别记为u1、u2和u3。 支路电压可用节点电压表示为: u12 = u1 – u2, u23 = u2 – u3, u13 = u1 – u3 , u14 = u1, u24 = u2, u34 = u3。 对电路的任意回路,如回路A,有 u13 – u23 – u12 = u1 – u3 – (u2 – u3 ) – (u1 – u2 )≡0 节点电压自动满足KVL方程。 节点电压的独立性 和完备性
2.4节点法 、节点法 3、节点法方程的列写规律 在节点1,2,3分别列出KCL方程:(设流出取正) 节点(1):i1+i2+is2+i4-is4=0 G2 节点(2):i3+i5-i2-is2=0 节点(3):i6+is6-i1-i3=0 根据OL将支路电流电流用节点电压表示 1S6 i1=G1(w1-w3),i2=G2(u1-w2),i3=G3(2-u3), i4=G4u1,i5=G52,i6=G6w3 代入KCL方程,合并整理后得 节点(1)(G1+G2+G4)u1 -G2u2 - Gn G12 G1 CIs) 节点(2) -G241+(G2+G3+G5)u2 G3u3= G21 G22 G23 节点(3) -G1u1 -G3u2+(G1+G3+G6)u3=-is6 G31 G32 G33 (1s3 15
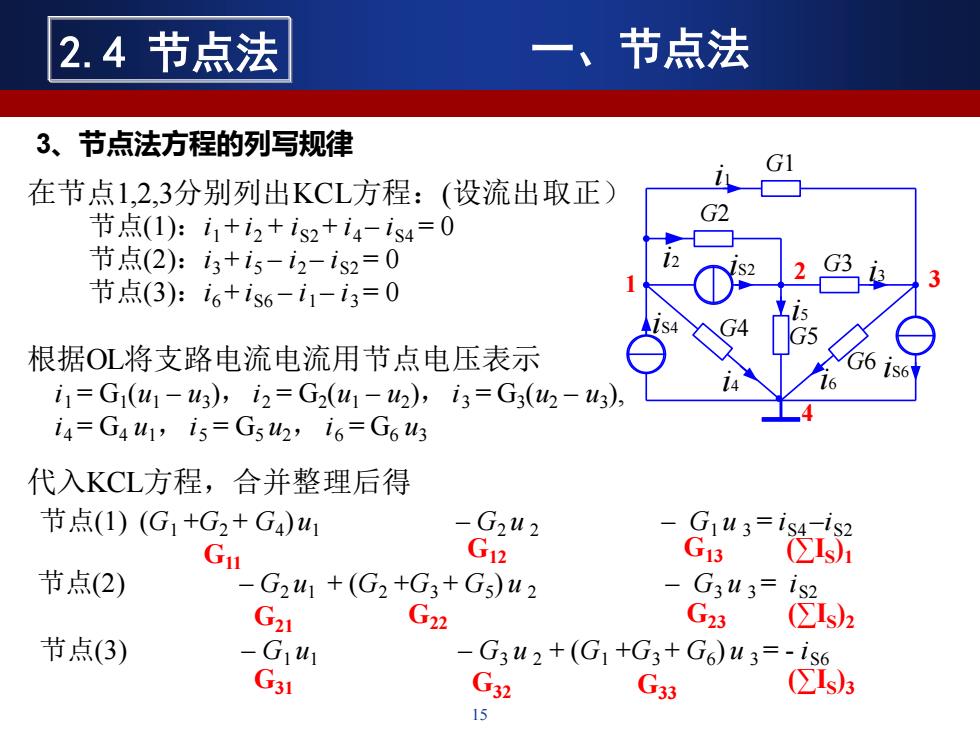
15 i4 G1 G2 G4 G6 1 i2 iS2 i5 G3 G5 iS4 iS6 2 3 4 i1 i3 i6 在节点1,2,3分别列出KCL方程:(设流出取正) 节点(1):i1 + i2 + iS2 + i4 – iS4 = 0 节点(2):i3 + i5 – i2 – iS2 = 0 节点(3):i6 + iS6 – i1 – i3 = 0 根据OL将支路电流电流用节点电压表示 i1 = G1 (u1 – u3 ), i2 = G2 (u1 – u2 ), i3 = G3 (u2 – u3 ), i4 = G4 u1, i5 = G5 u2, i6 = G6 u3 代入KCL方程,合并整理后得 节点(1) (G1 +G2 + G4 )u1 – G2 u 2 – G1 u 3 = iS4 –iS2 节点(2) – G2 u1 + (G2 +G3 + G5 ) u 2 – G3 u 3 = iS2 节点(3) – G1 u1 – G3 u 2 + (G1 +G3 + G6 ) u 3 = - iS6 G11 G22 G33 G12 G13 G21 G23 G31 G32 (∑IS )1 (∑IS )2 (∑IS )3 3、节点法方程的列写规律 2.4 节点法 一、节点法