
■给定作用 变化 R上 反馈控制系统具有良好的抗扰性能,它能 有效地抑制一切被负反馈环所包围的前向通 道上的扰动作用,但对给定作用则是唯命是 检清视出 从的。 与众不同的是在反锁环外的给定作用,如图中的 转速给定信号,它的些徽变化都会使被调量随之 变化,丝毫不受反馈作用的抑制。 S3.1.4闭环调速系统的反馈控制规律 ■结论: 3.系统的精度依赖于给定和反馈检测精度 给定精度一由于给定决定系统输出,输出精度自然取 反馈控制系统的规律是:一方面能够有 决于给定精度 效地地制一切被包围在负反幢环内邮向通 如果产生给定电压的电源发生波动,反债控制系统无 法鉴别是对给定电压的正常调节还是不应有的电压波动, 道上的忧功作用: 因此,高精度的调速系统必须有更高精度的给定稳压电 另一方面,紧紧地跟随着给定作用,对 源。 给定信号的任何变化都是唯命是从的。 检测辅度 一反绩检测装置的误差也是反债控制系统无 法克服的,因此检测精度决定了系统输出精度。 S3.1.5比例控制转速闭环系统的稳定性分析 §3,15比例控制转速闭环系统的稳定性分析 1比例控制直流调速系统的动态数学模型 。问题:增加比例调节器的比例系数,可以减小转速 、一个带有储能环节的线性物理系统的动态过程可以用线 降落,从而扩大调速范围。 性微分方程措述 5 。微分方程的解即系绕的动志过耀,它包括两部分:暂态 比钢系数可以感 响应和稳态响应。 。在动态过程中,从施加给定输入值的时刻开始,到输出 生意:设计系统首先要保证系统是稳定的】 达到稳态值以前,是系统的动态响应, 。系统达到稳态后, 可用稳态解来描述系统的稳态特性
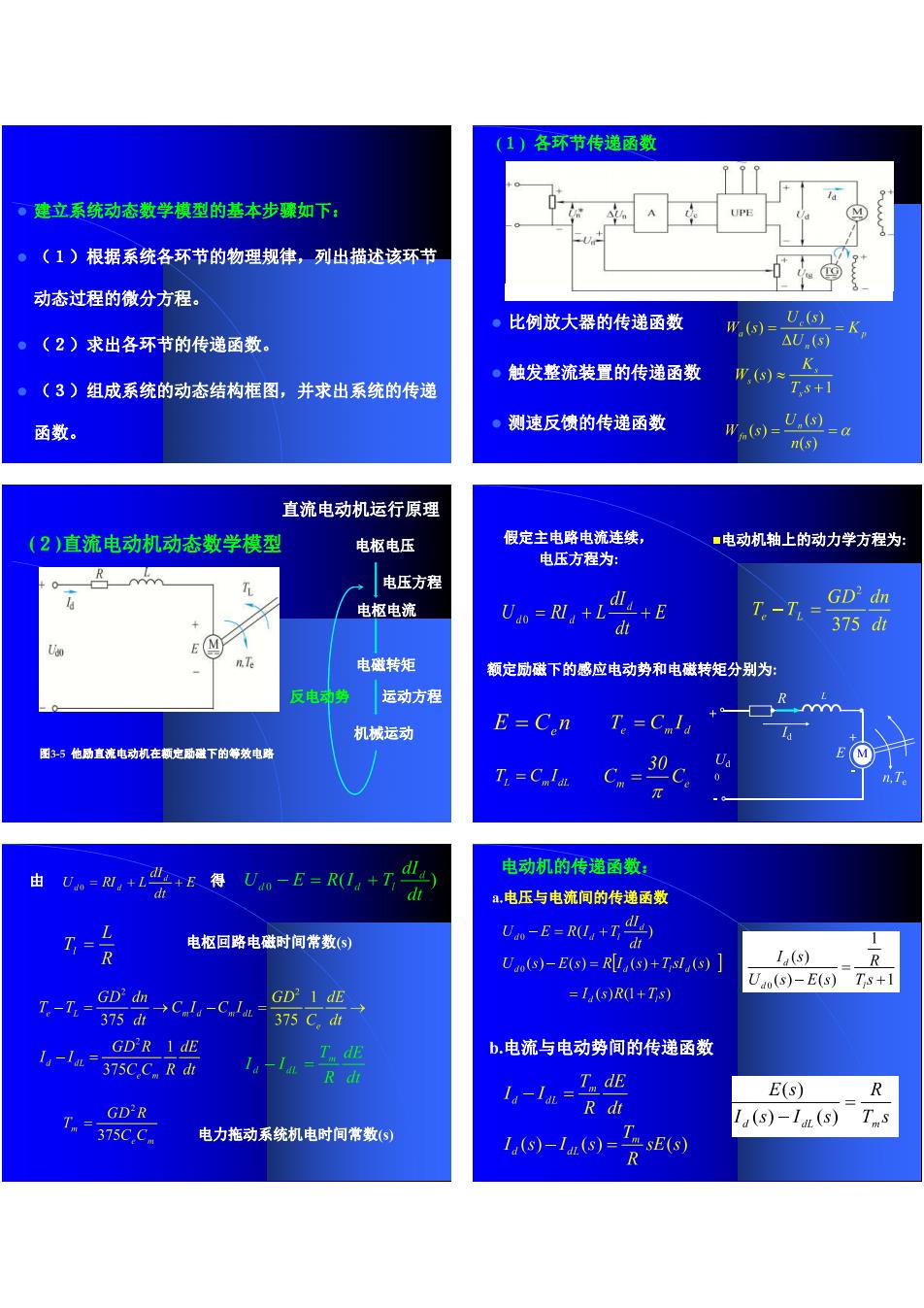
(1)各环节传递函数 。建立系统动态数学模型的基本步骤如下 ·(1)根据系统各环节的物理规律,列出描述该环节 动态过程的徽分方程。 ·比例放大器的传递函数 U.(s) 。(2)求出各环节的传递函数。 触发整流装置的传递函数 。(3)组成系统的动态结构框图,并求出系统的传递 函数。 ·测速反馈的传递函数 n(s) 直流电动机运行原理 (2)直流电动机动态数学模型 电据电压 假定主电路电流连续, ■电动机轴上的动力学方程为 电压方程为: 电压方程 Uw=刷+L GD dn 电枢电流 -+E T.-T=35d (M 电转矩 额定励磁下的感应电动势和电磁转矩分别为: 运动方程 R 机械运动 E=Cn T.=Cl 图35他扇直流电动机在 定磁下的等效电路 Tr =Cala 电动机的传递函数: 品,电压与电流间的传递函数 电枢回路电磁时间常数(付 -f,7尝 U)-E=R,+T,s)] L(s) GD'I dE =1()R+T Uao(s)-E(s)Ts+1 375d 375C,d GD'R I dE 1,-a-375C.C.R d T.de b.电流与电动势间的传递函数 R di E(s) R GD'R T.=375C.C. Rd山 I.(s)-Ia(s)Ts 电力施动系统机电时间常数何 1,-10= -sE(s)