
高等数学(下册)考试试卷(六)参考答案 、1、-》,2、6i+37+0:3、,fx+,fh: 1+y +、a6e;5V+x川+Gnd:6、-4mbcg 0-0*60-0:2g产,H<2 二、1、B:2、D;3、A:4、C;5、D6、C:7、C:8、A。 三◆6=22.则 G=RG=R,c石Ra-R0-1 于是过任意点P(x,0)处的切平面方程是: 2-0+2o-W-o+6-65Me-0 取x=a,y=b,:=c,上式被满足,即切平面过定点(a,b,c) [f=2(x-1)=0 四·=20-2)=0海在D内的鞋点M2. 令L=(x-1)2+0y-2)2+1+2x2+y2-20) =2x-0+2x=0 解方程组%三20V-2)+2=0得条件鞋点M24机M(2 0r+y-20-0 于是由f(M0=1,f(M)=6,f(M2)=46得所求的最大值为46,最小值为1。 五、如图D:sxs2 (ysxsy2
149 高等数学(下册)考试试卷(六)参考答案 一、1、 y x y + − 1 (1 ) 2 ;2、6i + 3 j + 0 k ;3、 + 1 ln 2 1 0 ln ln 2 1 ( , ) ( , ) 2 y e e e y y dy f x y dx dy f x y dx ; 4、 2 2 2 8 1 a b c ; 5、 z x y z x y dxdy x y 1 ( , ) ( , ) 2 2 + + ; 6、− 4abc ; 7、 1 1 2 2 2 3 1 c (y − y ) + c (y − y ) + y ; 8、 , 2 4 ( 1) 0 2 1 − = + x x n n n n 二、1、B; 2、D ; 3、A; 4、C; 5、D; 6、C; 7、C; 8、A。 三、令 ( , ) z c y b z c x a G F − − − − = ,则 x Fu z c G − = 1 , y Fv z c G − = 1 , [ ( ) ( )] ( ) 1 2 F x a F y b z c Gz u − + v − − = − 于是过任意点 ( , , ) 0 0 0 P x y z 处的切平面方程是: ( ) ( ) 0 0 x x z c Fu P − − − − − + ( ) ( ) 0 0 y y z c Fv P [( ) ( ) ( ) ( )]( ) 0 ( ) 1 2 0 0 0 0 − + − − = − x a F P y b F P z z z c u v 取 x = a, y = b,z = c ,上式被满足,即切平面过定点 (a,b, c) 四、 = − = = − = 2( 2) 0 2( 1) 0 f y f x y x 得 f (x, y) 在 D 内的驻点 M (1,2) , 令 ( 1) ( 2) 1 ( 20) 2 2 2 2 L = x − + y − + + x + y − 解方程组 = + − = = − + = = − + = 20 0 2( 2) 2 0 2( 1) 2 0 2 2 x y L y y y L x x x L 得条件驻点 (2,4), ( 2, 4) M1 M2 − − 于是由 f (M) =1, f (M1 ) = 6, f (M2 ) = 46 得所求的最大值为 46,最小值为 1。 五、如图 2 1 2 : y x y x D
所1-m六 四 =ji1-头扩 3 0 -ow-n受+om =2+): 六令r=R+y+F,P=于Q=片R=月 于是P+巴+那-0≠0m 作辅助曲面Σ,:x2+y2+:2=62,内侧,6使得8位于的内部,以2表示由2与Σ。 所围成的立体域,2,表示工。所围成的立体域,则 =Ⅱ+川-川 w公式架+器+-打++ 83 =0-川+t本+how公式-川3=-是音-标 七、因为一c=1,所以技积函数连续。 又acnW=中子2rkd am=亭2-r产k25Hs1 多
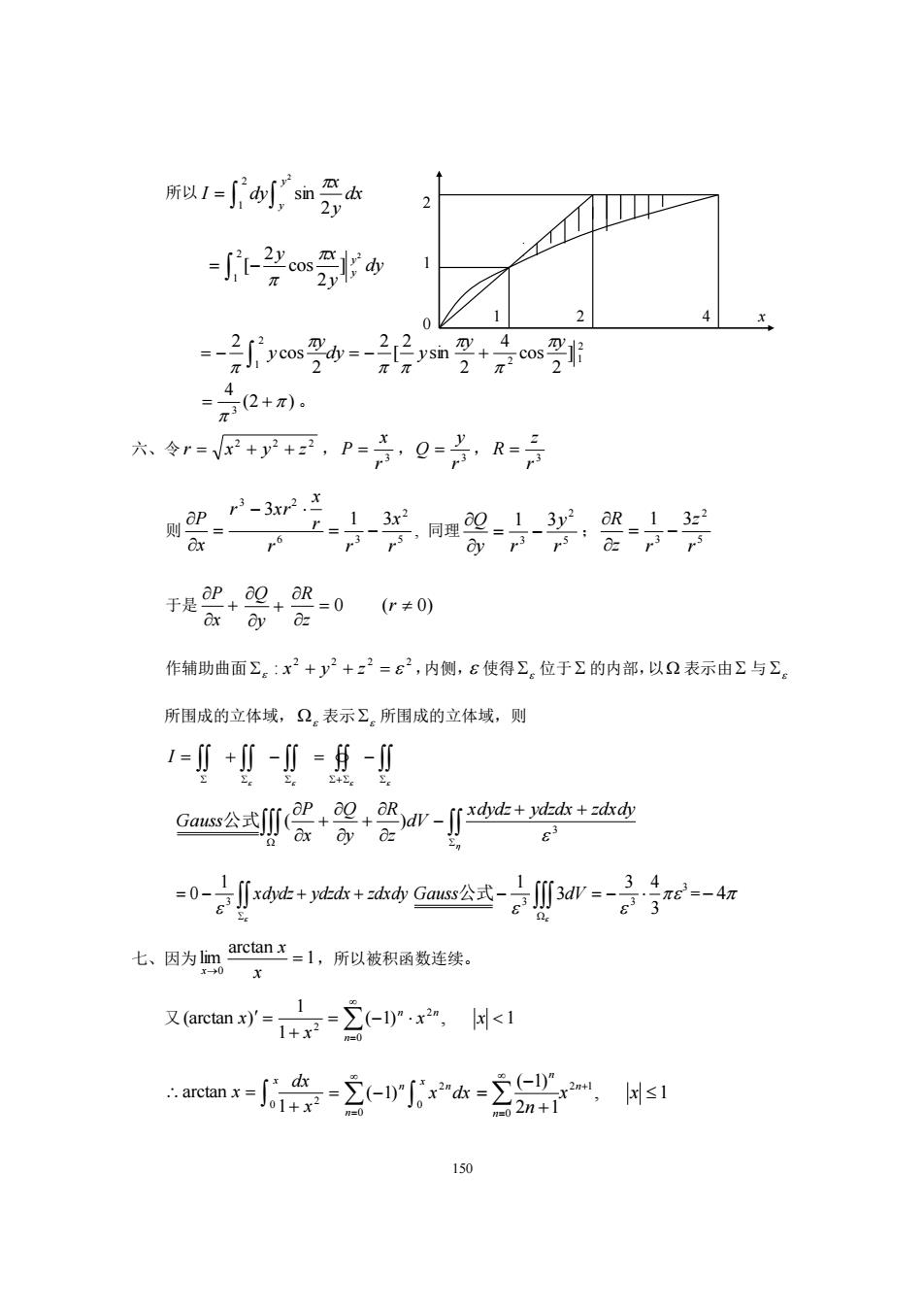
150 所以 = 2 1 2 2 sin y y dx y x I dy dy y y x y y 2 ] 2 cos 2 [ 2 1 = − 2 2 1 2 1 ] 2 cos 4 2 sin 2 [ 2 2 cos 2 y y dy y y y = − = − + (2 ) 4 3 = + 。 六、令 2 2 2 r = x + y + z , 3 r x P = , 3 r y Q = , 3 r z R = 则 5 2 6 3 3 2 1 3 3 r x r r r x r xr x P = − − = , 同理 5 2 3 1 3 r y y r Q = − ; 5 2 3 1 3 r z z r R = − 于是 + x P + y Q = 0 ( 0) r z R 作辅助曲面 2 2 2 2 : x + y + z = ,内侧, 使得 位于 的内部,以 表示由 与 所围成的立体域, 表示 所围成的立体域,则 + = + − = − I + + − + + 3 ( ) xdydz ydzdx zdxdy dV z R y Q x P Gauss公式 = − + + xdydz ydzdx zdxdy 3 1 0 3 3 3 3 3 4 3 1 − = − Gauss公式 dV = − 4 七、因为 1 arctan lim 0 = → x x x ,所以被积函数连续。 又 ( 1) , 1 1 1 (arctan ) 2 0 2 = − + = = x x x x n n n + = x x dx x 0 2 1 arctan = = − x n n n x dx 0 2 0 ( 1) , 1 2 1 ( 1) 2 1 0 + − = + = x x n n n n 2 1 0 1 2 4 x