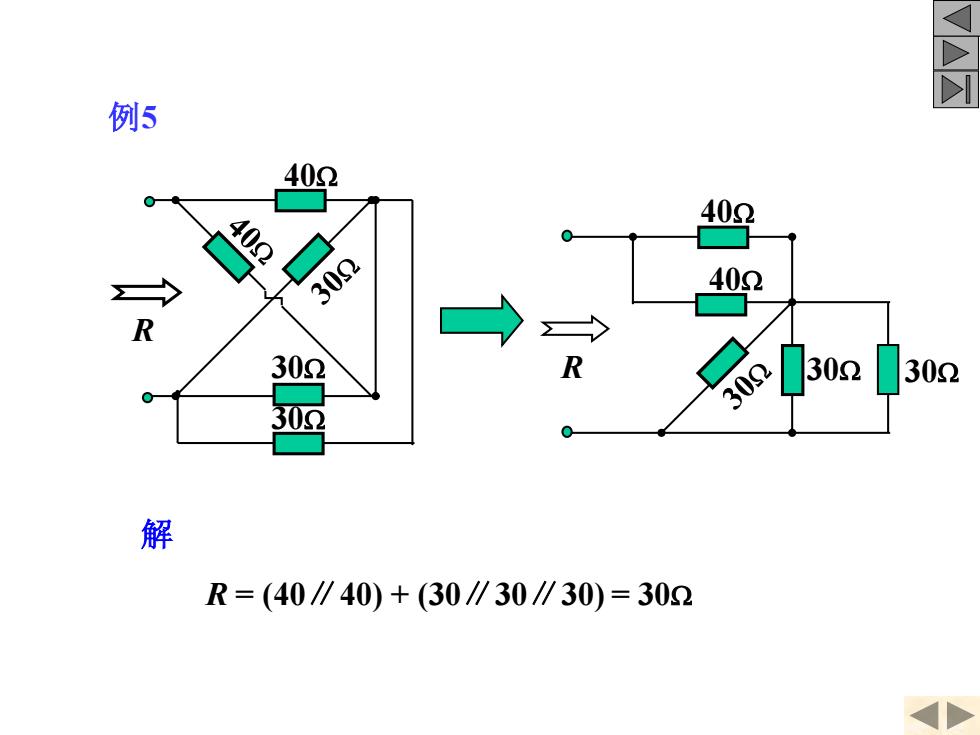
D I 例5 402 402 402 30 402 R 302 0 30 2302 302 0 解 R=(40∥40)+(30∥30∥30)=302
解 R = (40∥40) + (30∥30∥30) = 30W 例5 40W 30W 30W R 40W 40W R 30W 30W
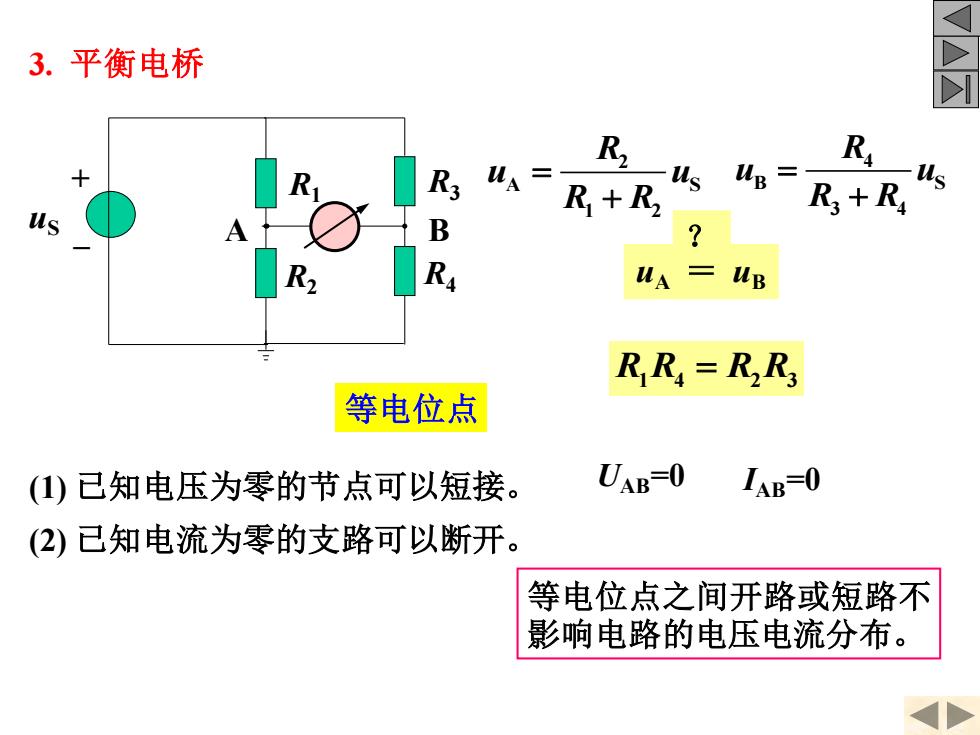
3.平衡电桥 WA= R R R3 R+R -us us up=R+R B R RR=RR 等电位点 (1)已知电压为零的节点可以短接。 UAB-0 IAB=0 (2)已知电流为零的支路可以断开。 等电位点之间开路或短路不 影响电路的电压电流分布
R1 R2 R3 R4 + _ uS A B 2 A S 1 2 R u u R R = + 4 B S 3 4 R u u R R = + uA = uB ? R R R R 1 4 2 3 = UAB=0 IAB=0 (2) 已知电流为零的支路可以断开。 (1) 已知电压为零的节点可以短接。 等电位点 等电位点之间开路或短路不 影响电路的电压电流分布。 3. 平衡电桥
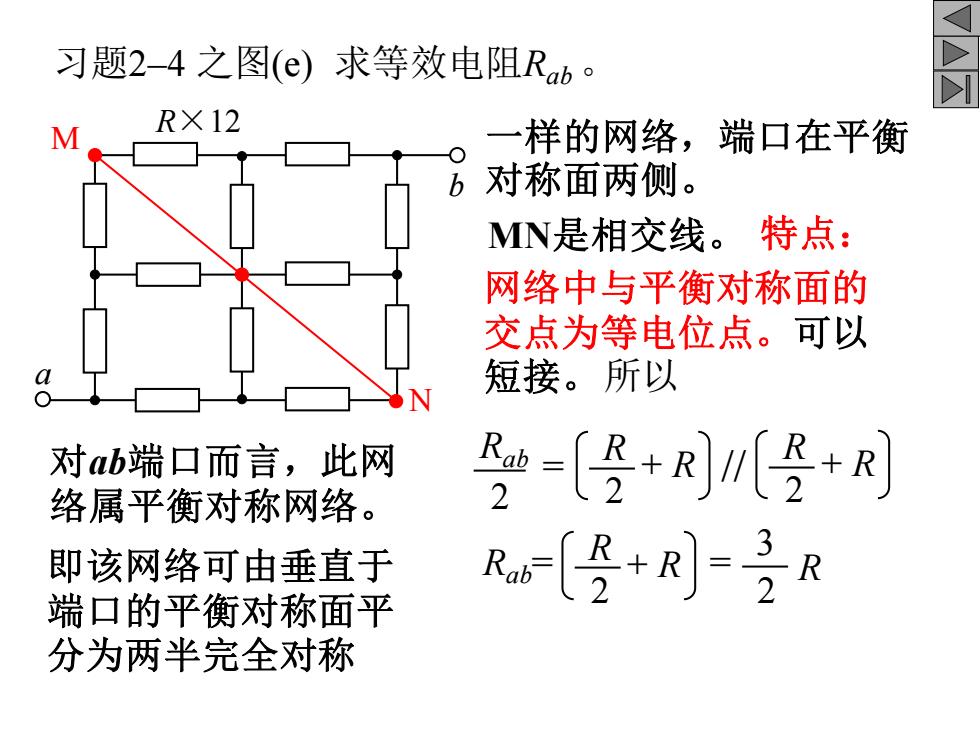
习题2-4之图(e)求等效电阻Rb。 R×12 一样的网络,端口在平衡 b对称面两侧。 MN是相交线。特点: 网络中与平衡对称面的 交点为等电位点。可以 短接。所以 对ab端口而言,此网 R=〔+R[5+R 络属平衡对称网络。 即该网络可由垂直于 Rb-(5+R=3R 端口的平衡对称面平 分为两半完全对称
习题2–4 之图(e) 求等效电阻Rab 。 R×12 b a Rab 2 = 2 R + R // 2 R + R Rab= 2 R + R = 2 3 R M N 对ab端口而言,此网 络属平衡对称网络。 即该网络可由垂直于 端口的平衡对称面平 分为两半完全对称 一样的网络,端口在平衡 对称面两侧。 MN是相交线。 网络中与平衡对称面的 交点为等电位点。可以 短接。 特点: 所以
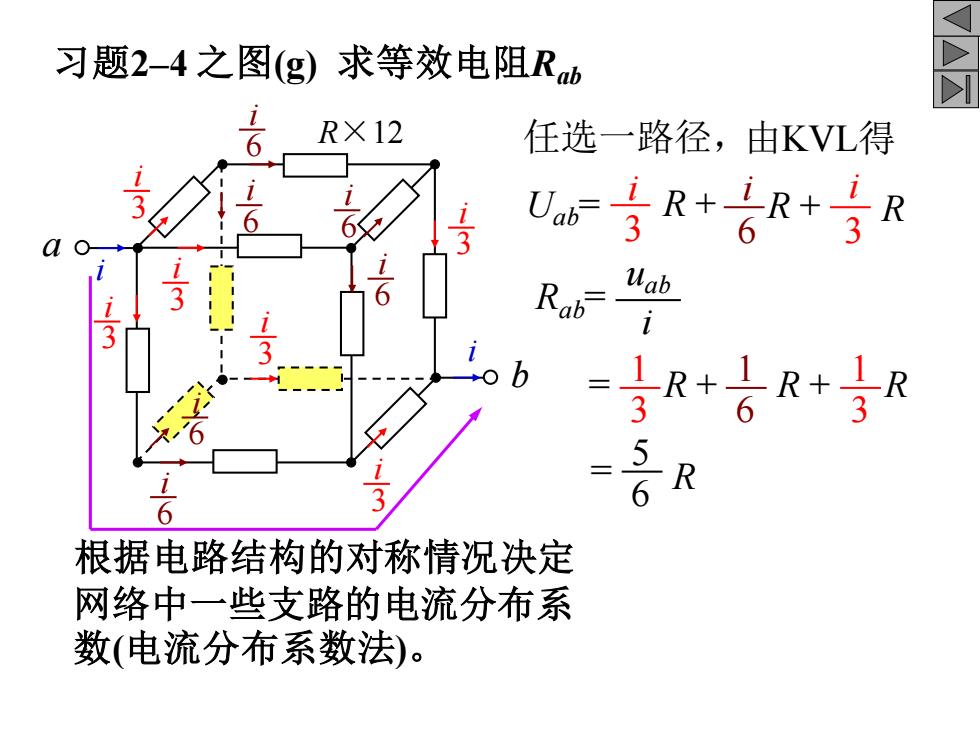
习题2-4之图(g)求等效电阻Rb -6 RX12 任选一路径,由KVL得 U=号R+名R+号R 3 Rab D 6 根据电路结构的对称情况决定 网络中一些支路的电流分布系 数(电流分布系数法)
习题2–4 之图(g) 求等效电阻Rab 根据电路结构的对称情况决定 网络中一些支路的电流分布系 数(电流分布系数法)。 a b R×12 i i 3 i 3 i 3 i i 3 i i 3 3 i 6 i 6 i 6 i 6 i 6 i 6 Uab= 3 i R + 6 i R + 3 i R Rab= uab i = 3 1 R + 6 1 R + 3 1 R = 6 5 R 任选一路径,由KVL得