
9.4最佳平方逼近与正交多项式 如 解取函数空间M=span{1,工,x2,由定理9.8知,二次最佳平方逼近多项式5()存 在且唯一.据式(9.12),取权函数p(x)=1,容易算得 (p0,p0)=1,(p0,p1)=1/2,(p0,p2=1/3. (p1,p0)=1/2,(p1,p1)=1/3,(p1,p2)=1/4 (p2,90)=1/3,(p2,p)=1/4,(p2,p2)=1/5, Gl-人m(山=是 xsin()dr= 1 (f,p)= 乐网)-厂rm(a)山-24 分3 故p(x)=c0+91x+c2:x2满足法方程 1 11Y 2 3 1 21 34 3 求解出 =122-120≈-050465.1=720-602 T3 元3 ≈4.12251,c2=-c1≈-4.12251. 因此,p5(x)≈-0.050465+4.12251x-4.12251x2,逼近情况如图9.2所示. 当[a,=[0,1,p(x)=1时,法方程组(9.12)的系数矩阵是 1 n+1n+2 2n+1/ H称为希尔伯特(Hilbert))矩阵.当n较大时,可以证明H是病态的.因此,对于许多实 际问题来说,通过法方程来确定函数的最佳平方逼近多项式是有困难的.然而,通过分
9.4 最佳平方逼近与正交多项式 19 解 取函数空间 M = span{1, x, x2}, 由定理9.8知, 二次最佳平方逼近多项式 p ∗ 2 (x) 存 在且唯一. 据式 (9.12), 取权函数 ρ(x) = 1, 容易算得 (φ0, φ0) = 1, (φ0, φ1) = 1/2, (φ0, φ2) = 1/3, (φ1, φ0) = 1/2, (φ1, φ1) = 1/3, (φ1, φ2) = 1/4, (φ2, φ0) = 1/3, (φ2, φ1) = 1/4, (φ2, φ2) = 1/5, (f, φ0) = ∫ 1 0 sin(πx) dx = 2 π , (f, φ1) = ∫ 1 0 x sin(πx) dx = 1 π , (f, φ2) = ∫ 1 0 x 2 sin(πx) dx = π 2 − 4 π 3 , 故 p ∗ 2 (x) = c0 + c1x + c2x 2 满足法方程 1 1 2 1 3 1 2 1 3 1 4 1 3 1 4 1 5 c0 c1 c2 = 2 π 1 π π 2 − 4 π 3 求解出 c0 = 12π 2 − 120 π 3 ≈ −0.050465, c1 = 720 − 60π 2 π 3 ≈ 4.12251, c2 = −c1 ≈ −4.12251. 因此, p ∗ 2 (x) ≈ −0.050465 + 4.12251x − 4.12251x 2 , 逼近情况如图9.2所示. 当 [a, b] = [0, 1], ρ(x) = 1 时, 法方程组 (9.12) 的系数矩阵是 H = 1 1 2 · · · 1 n 1 2 1 3 · · · 1 n + 1 . . . . . . . . . . . . 1 n + 1 1 n + 2 · · · 1 2n + 1 , H 称为希尔伯特 (Hilbert) 矩阵. 当 n 较大时, 可以证明 H 是病态的. 因此, 对于许多实 际问题来说, 通过法方程来确定函数的最佳平方逼近多项式是有困难的. 然而, 通过分�
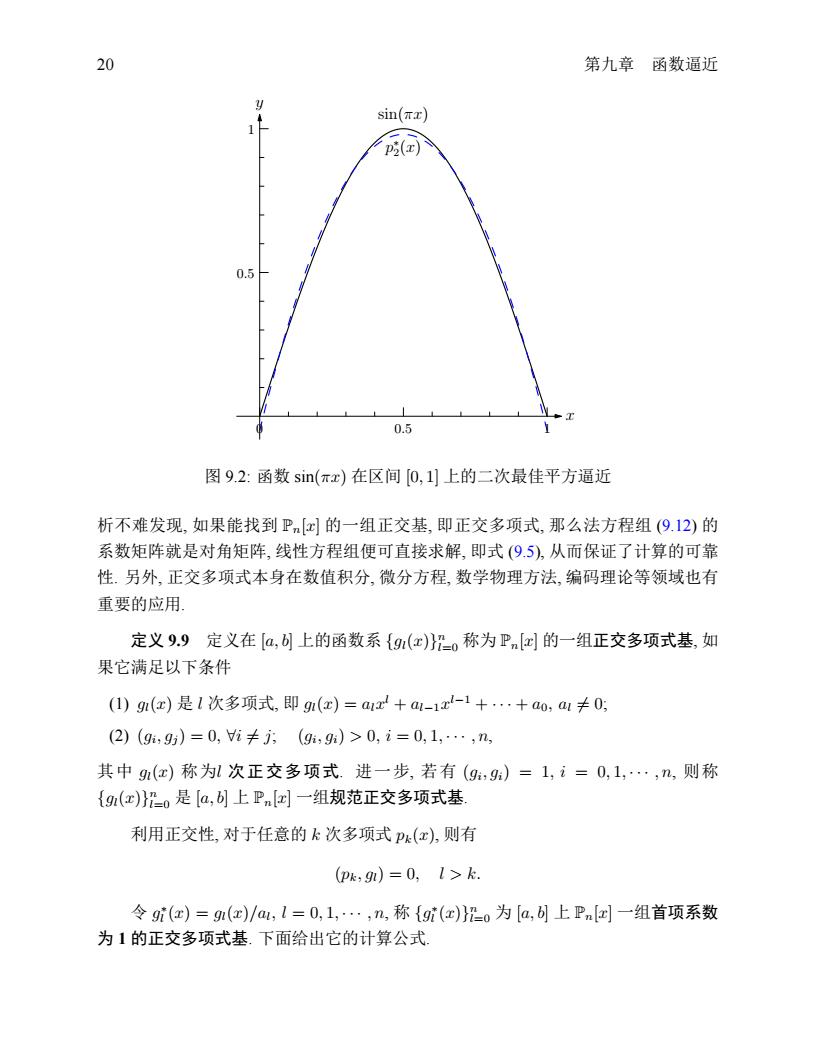
20 第九章函数逼近 sin(r) ( 0.5 图92:函数sin(rx)在区间0,1上的二次最佳平方逼近 析不难发现,如果能找到Pd的一组正交基,即正交多项式,那么法方程组(9.12)的 系数矩阵就是对角矩阵,线性方程组便可直接求解,即式(9.5),从而保证了计算的可靠 性.另外,正交多项式本身在数值积分,微分方程,数学物理方法,编码理论等领域也有 重要的应用 定义9.9定义在[a,)上的函数系{9(x)}o称为Pn回的一组正交多项式基,如 果它满足以下条件 (1)g9(x)是1次多项式,即gm(x)=a1x+a1-1x-1+…+a0,a1≠0 (2)(g,9)=0,i≠j;(g,9)>0,i=0,1,…,n 其中gn()称为次正交多项式.进一步,若有(99)=1,i=0,1,…,n,则称 {g(x)}”o是[a,上Pna一组规范正交多项式基 利用正交性,对于任意的k次多项式P4(x),则有 (pk,)=0,1>k. 令gi(x)=g(x)/au,1=0,L,…,n,称{g(x)}o为[a,上Pn回一组首项系数 为1的正交多项式基.下面给出它的计算公式
20 第九章 函数逼近 sin(πx) p ∗ 2 (x) 0 0.5 1 x 0.5 1 y 图 9.2: 函数 sin(πx) 在区间 [0, 1] 上的二次最佳平方逼近 析不难发现, 如果能找到 Pn[x] 的一组正交基, 即正交多项式, 那么法方程组 (9.12) 的 系数矩阵就是对角矩阵, 线性方程组便可直接求解, 即式 (9.5), 从而保证了计算的可靠 性. 另外, 正交多项式本身在数值积分, 微分方程, 数学物理方法, 编码理论等领域也有 重要的应用. 定义 9.9 定义在 [a, b] 上的函数系 {gl(x)} n l=0 称为 Pn[x] 的一组正交多项式基, 如 果它满足以下条件 (1) gl(x) 是 l 次多项式, 即 gl(x) = alx l + al−1x l−1 + · · · + a0, al ̸= 0; (2) (gi , gj ) = 0, ∀i ̸= j; (gi , gi) > 0, i = 0, 1, · · · , n, 其中 gl(x) 称为l 次正交多项式. 进一步, 若有 (gi , gi) = 1, i = 0, 1, · · · , n, 则称 {gl(x)} n l=0 是 [a, b] 上 Pn[x] 一组规范正交多项式基. 利用正交性, 对于任意的 k 次多项式 pk(x), 则有 (pk, gl) = 0, l > k. 令 g ∗ l (x) = gl(x)/al , l = 0, 1, · · · , n, 称 {g ∗ l (x)} n l=0 为 [a, b] 上 Pn[x] 一组首项系数 为 1 的正交多项式基. 下面给出它的计算公式

9.4最佳平方逼近与正交多项式 3 定理9.12正交多项式基{9(x)}”o有递推公式: ∫6国=1,9i国=1-的90 (xg6,96) (9.13) g(x)=(x-ak)g底-1(x)-bs9底-2(x),k=2,3,…,n, 中一贸签含 证明从递推关系式(9.13),不难看出g(x)是首项系数为1的多项式,故均不为零. 于是在ak与b:公式中的分母皆非零.下面用数学归纳法来证明(g,9)=0,对任意 的整数i<n成立. 当n=1时,容易验证 (gi,96)=(x-a1,96)=(x,96)-(a1,g6) =(x,9g6)-(xg6,g)=0. 假设命题对n-1成立,那么 (gn,9i-1)=(rgn-1-an9i-1-bn9h-2:9-i) =(xgn-19h-1)-a(gh-19n-i)=0. 类似地有 (gn,9n-2)=(xgn-1-an9n-1-bn9gn-2,9n-2) =(xgn-19h-2)-bn(gn-2,9h-2)=0. 而对于i<n-2,我们有 (g,g)=(xgi-1-ang9i-1-bngi-2g)=(x9-1,9) =(ga-1,x9)=(gn-1,9+1+a4+19+b+19-1)=0. 从而定理得证 下面,我们证明一个非常有用的结论. 定理9.13若f(x)为[a,上任一连续函数,与g6(x),9(z),·,9(x)都正交,则 f(x)在(a,b)中至少变号n+1次或者恒等于零
9.4 最佳平方逼近与正交多项式 21 定理 9.12 正交多项式基 {g ∗ l (x)} n l=0 有递推公式: g ∗ 0 (x) = 1, g∗ 1 (x) = x − (xg∗ 0 , g∗ 0 ) (g ∗ 0 , g∗ 0 ) , g ∗ k (x) = (x − ak)g ∗ k−1 (x) − bkg ∗ k−2 (x), k = 2, 3, · · · , n, (9.13) 其中 ak = (xg∗ k−1 , g∗ k−1 ) (g ∗ k−1 , g∗ k−1 ) , bk = (xg∗ k−1 , g∗ k−2 ) (g ∗ k−2 , g∗ k−2 ) . 证明 从递推关系式 (9.13), 不难看出 g ∗ k (x) 是首项系数为 1 的多项式, 故均不为零. 于是在 ak 与 bk 公式中的分母皆非零. 下面用数学归纳法来证明 (g ∗ n , g∗ i ) = 0, 对任意 的整数 i < n 成立. 当 n = 1 时, 容易验证 (g ∗ 1 , g∗ 0 ) = (x − a1, g∗ 0 ) = (x, g∗ 0 ) − (a1, g∗ 0 ) = (x, g∗ 0 ) − (xg∗ 0 , g∗ 0 ) = 0. 假设命题对 n − 1 成立, 那么 (g ∗ n , g∗ n−1 ) = (xg∗ n−1 − ang ∗ n−1 − bng ∗ n−2 , g∗ n−1 ) = (xg∗ n−1 , g∗ n−1 ) − an(g ∗ n−1 , g∗ n−1 ) = 0. 类似地有 (g ∗ n , g∗ n−2 ) = (xg∗ n−1 − ang ∗ n−1 − bng ∗ n−2 , g∗ n−2 ) = (xg∗ n−1 , g∗ n−2 ) − bn(g ∗ n−2 , g∗ n−2 ) = 0. 而对于 i < n − 2, 我们有 (g ∗ n , g∗ i ) = (xg∗ n−1 − ang ∗ n−1 − bng ∗ n−2 , g∗ i ) = (xg∗ n−1 , g∗ i ) = (g ∗ n−1 , xg∗ i ) = (g ∗ n−1 , g∗ i+1 + ai+1g ∗ i + bi+1g ∗ i−1 ) = 0. 从而定理得证. 下面, 我们证明一个非常有用的结论. 定理 9.13 若 f(x) 为 [a, b] 上任一连续函数, 与 g ∗ 0 (x), g∗ 1 (x), · · · , g∗ n (x) 都正交, 则 f(x) 在 (a, b) 中至少变号 n + 1 次或者恒等于零.�

Y 第九章函数逼近 证明因f⊥96,且g6=1,故 p(z)f(x)dz=0. 于是,若f≠0,则f(x)在(a,b)中至少变号一次. 若f(x)在(a,b)中变号k次,且k<n+1.令x1<x2<…<xk为(a,b)中f(x) 发生变号的点,则在每个区间(a,x1),(x1,x2),…,(ck,b)中f(x)不变号,但在相邻的 区间内符号相反.令k次多项式p(x)=(x-x),显然p(x)亦具有此性质.于是 i=1 。Da)f(z)p(e)dtr≠o. 另一方面,因fx)与96(x),9(x),…,9(x)都正交,故f(x)与p(x)正交,这与上式相 矛盾 推论9.14若f(x)为[a,上任一连续函数,p(x)是f(z)的n次最佳平方逼近多 项式,则p(x)在(a,b)中至少n+1个点插值于fx) 证明因(x)是∫(x)的最佳平方逼近多项式,利用定理(9.9),知(p-f)(x)与 g96(x),9i(x),·,9(x)都正交.利用定理(9.13),推论得证。 与一般的多项式不同,正交多项式的零点具有很好的性质 定理9.15区间[a,)上的1次正交多项g(x)恰有1个互异的实根,并且全部位 于[a,的内部 证明因听(四)与9()9i(),…,9-1国)都正交,且g旷()是首项系数为1的多项 式,利用定理(9.13),知g(x)在(a,b)中至少变号1次.又利用代数基本定理,知g(x) 在复数域C具有1个根.于是,推论得证 ■ 最后,给出几类常用的带权正交多项式 I)勒让德(Legendre)多项式 设p(x)三1,区间[-1,1上Pn(z)的正交基{P(x)}R=o,称P(x)为勒让德多项 式.利用正交多项式的定义,可写出P(x)的解析表达式: A间=e-y明,k=an (9.14)
22 第九章 函数逼近 证明 因 f ⊥ g ∗ 0 , 且 g ∗ 0 = 1, 故 ∫ b a ρ(x)f(x) dx = 0. 于是, 若 f ̸= 0, 则 f(x) 在 (a, b) 中至少变号一次. 若 f(x) 在 (a, b) 中变号 k 次, 且 k < n + 1. 令 x1 < x2 < · · · < xk 为 (a, b) 中 f(x) 发生变号的点, 则在每个区间 (a, x1),(x1, x2), · · · ,(xk, b) 中 f(x) 不变号, 但在相邻的 区间内符号相反. 令 k 次多项式 p(x) = ∏ k i=1 (x − xi), 显然 p(x) 亦具有此性质. 于是 ∫ b a ρ(x)f(x)p(x) dx ̸= 0. 另一方面, 因 f(x) 与 g ∗ 0 (x), g∗ 1 (x), · · · , g∗ n (x) 都正交, 故 f(x) 与 p(x) 正交, 这与上式相 矛盾. 推论 9.14 若 f(x) 为 [a, b] 上任一连续函数, p(x) 是 f(x) 的 n 次最佳平方逼近多 项式, 则 p(x) 在 (a, b) 中至少 n + 1 个点插值于 f(x). 证明 因 p(x) 是 f(x) 的最佳平方逼近多项式, 利用定理 (9.9), 知 (p − f)(x) 与 g ∗ 0 (x), g∗ 1 (x), · · · , g∗ n (x) 都正交. 利用定理 (9.13), 推论得证. 与一般的多项式不同, 正交多项式的零点具有很好的性质. 定理 9.15 区间 [a, b] 上的 l 次正交多项 g ∗ l (x) 恰有 l 个互异的实根, 并且全部位 于 [a, b] 的内部. 证明 因 g ∗ l (x) 与 g ∗ 0 (x), g∗ 1 (x), · · · , g∗ l−1 (x) 都正交, 且 g ∗ l (x) 是首项系数为 1 的多项 式, 利用定理 (9.13), 知 g ∗ l (x) 在 (a, b) 中至少变号 l 次. 又利用代数基本定理, 知 g ∗ l (x) 在复数域 C 具有 l 个根. 于是, 推论得证. 最后, 给出几类常用的带权正交多项式. 1) 勒让德 (Legendre) 多项式 设 ρ(x) ≡ 1, 区间 [−1, 1] 上 Pn(x) 的正交基 {Pk(x)} n k=0, 称 Pk(x) 为勒让德多项 式. 利用正交多项式的定义, 可写出 Pk(x) 的解析表达式: Pk(x) = 1 2 kk! d k dx k [ (x 2 − 1)k ] , k = 0, 1, · · · , n. (9.14)���

9.4最佳平方逼近与正交多项式 2 实际应用中,因为求高阶导数较麻烦,所以使用下面递推公式计算: n国=n国-点A,=12m (9.15) 利用上式,不难证明,当k为偶数时,P(x)为偶函数;当k为奇数时,P(x)为奇 函数 2)第一类切比雪夫(Chebyshev)多项式 设p(x)=(1-x2)-1/2,区间[-1,1刂上Pn(x)的正交基{Tk(x}=0,称Tk(x)为第 一类切比雪夫多项式.利用正交多项式的定义,可写出T(x)的解析表达式: Tk()=cos(k arccos ),k=0,1,...,n. (9.16) 由三角恒等式cosk0+cos(k-2)9=2cos0cos(k-1)0,可得Tk(x)的递推计算 公式: T+1(x)=2xTk(x)-Tk-1(x),k=1,2,·,n, (9.17) T(x)=1,T(x)=x. 利用数学归纳法,容易证明,Tk(x)是首项系数为2*-1的k次多项式,且T2只含 x的偶次幂,T2k-1只含x的奇次幂. 3)第二类切比雪夫(Chebyshev)多项式 设p(x)=(1-x2)1/2,区间[-1,1川上Pn(e)的正交基{U(x)=o,称U(x)为第 二类切比雪夫多项式.第二类切比雪夫多项式的解析表达式 回=mk+)rcs,k=01,,m (9.18) 1-x2 Ux(x)的递推计算公式 U+1(x)=2xU(x)-U-1(e),k=1,2,…,n, (9.19) Uo(x)=1,U1(x)=2x. 4)拉盖尔(Laguerre)多项式 设p(x)=e,区间0,+o∞)上Pn(x)的正交基{Lk(x)}=o,称Lk(x)为拉盖尔 多项式.拉盖尔多项式的解析表达式 d Lk(r)=e* de,k=0,1,…,n (9.20)
9.4 最佳平方逼近与正交多项式 23 实际应用中, 因为求高阶导数较麻烦, 所以使用下面递推公式计算: Pk+1(x) = 2k + 1 k + 1 xPk(x) − k k + 1 Pk−1(x), k = 1, 2, · · · , n. (9.15) 利用上式, 不难证明, 当 k 为偶数时, Pk(x) 为偶函数; 当 k 为奇数时, Pk(x) 为奇 函数. 2) 第一类切比雪夫 (Chebyshev) 多项式 设 ρ(x) = (1 − x 2 ) −1/2 , 区间 [−1, 1] 上 Pn(x) 的正交基 {Tk(x)} n k=0, 称 Tk(x) 为第 一类切比雪夫多项式. 利用正交多项式的定义, 可写出 Tk(x) 的解析表达式: Tk(x) = cos(k arccos x), k = 0, 1, · · · , n. (9.16) 由三角恒等式 cos kθ + cos(k − 2)θ = 2 cos θ cos(k − 1)θ, 可得 Tk(x) 的递推计算 公式: Tk+1(x) = 2xTk(x) − Tk−1(x), k = 1, 2, · · · , n, T0(x) = 1, T1(x) = x. (9.17) 利用数学归纳法, 容易证明, Tk(x) 是首项系数为 2 k−1 的 k 次多项式, 且 T2k 只含 x 的偶次幂, T2k−1 只含 x 的奇次幂. 3) 第二类切比雪夫 (Chebyshev) 多项式 设 ρ(x) = (1 − x 2 ) 1/2 , 区间 [−1, 1] 上 Pn(x) 的正交基 {Uk(x)} n k=0, 称 Uk(x) 为第 二类切比雪夫多项式. 第二类切比雪夫多项式的解析表达式 Uk(x) = sin[(k + 1) arccos x] √ 1 − x 2 , k = 0, 1, · · · , n. (9.18) Uk(x) 的递推计算公式: Uk+1(x) = 2xUk(x) − Uk−1(x), k = 1, 2, · · · , n, U0(x) = 1, U1(x) = 2x. (9.19) 4) 拉盖尔 (Laguerre) 多项式 设 ρ(x) = e −x , 区间 [0, +∞) 上 Pn(x) 的正交基 {Lk(x)} n k=0, 称 Lk(x) 为拉盖尔 多项式. 拉盖尔多项式的解析表达式 Lk(x) = e x d k dx k (x k e −x ), k = 0, 1, · · · , n. (9.20)