14 第九章函数逼近 x1315162122232529303116 %1110111212131312141617 x:4042556062647072100130 13142214212124172334 表9.1:鱼的数量和种类,其中x为鱼的数量,y为鱼的种类 试用线性函数拟合鱼的数量和种类之间的关系, 解设p(x)=c0+C1工,则线性函数拟合的法方程组为 将表9.1中的数据代入并求解得 即p(x)=8.20841+0.17952x,输入数据和拟合函数如图9.1所示」 ◇ 0 40 30 20f 11L111L1上1L11上L上11L上上上L11山 0 20 40 60 80100120140 图9.1:线性函数拟合 更多的例子
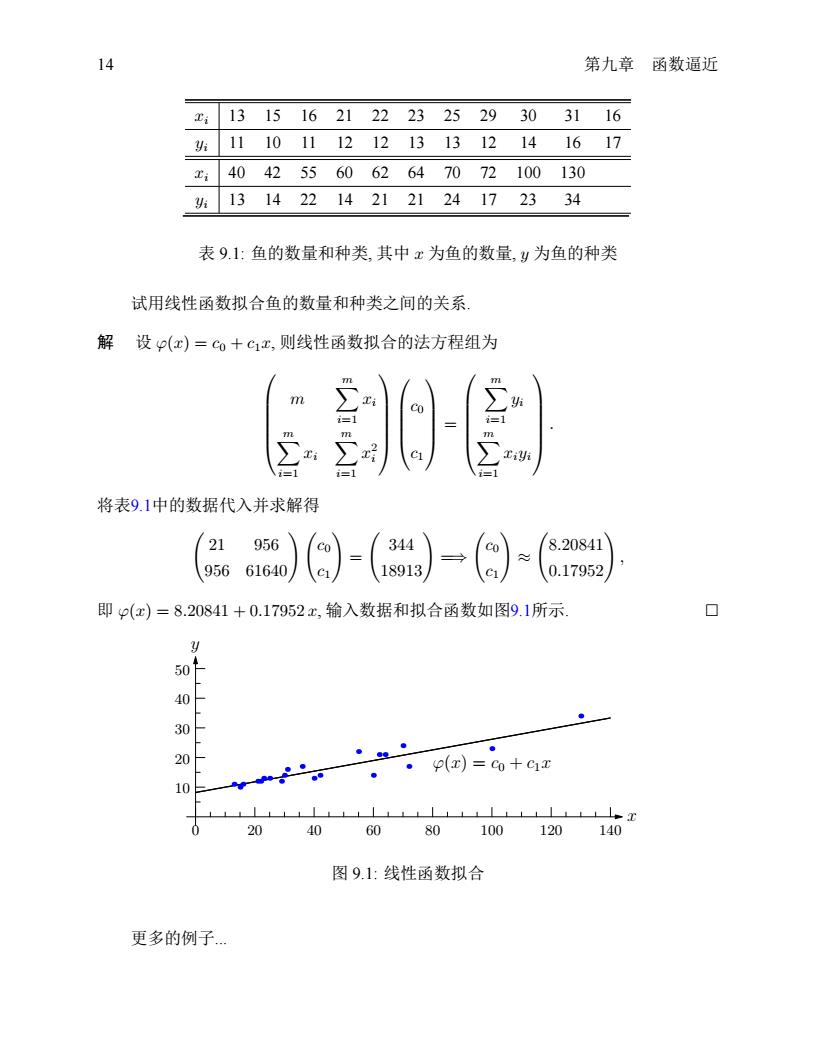
14 第九章 函数逼近 xi 13 15 16 21 22 23 25 29 30 31 16 yi 11 10 11 12 12 13 13 12 14 16 17 xi 40 42 55 60 62 64 70 72 100 130 yi 13 14 22 14 21 21 24 17 23 34 表 9.1: 鱼的数量和种类, 其中 x 为鱼的数量, y 为鱼的种类 试用线性函数拟合鱼的数量和种类之间的关系. 解 设 φ(x) = c0 + c1x, 则线性函数拟合的法方程组为 m ∑m i=1 xi ∑m i=1 xi ∑m i=1 x 2 i c0 c1 = ∑m i=1 yi ∑m i=1 xiyi . 将表9.1中的数据代入并求解得 ( 21 956 956 61640) (c0 c1 ) = ( 344 18913) =⇒ ( c0 c1 ) ≈ ( 8.20841 0.17952) , 即 φ(x) = 8.20841 + 0.17952 x, 输入数据和拟合函数如图9.1所示. ϕ(x) = c0 + c1x 0 20 40 60 80 100 120 140 x 10 20 30 40 50 y 图 9.1: 线性函数拟合 更多的例子...�

9.3最小二乘法 15 前面主要讨论了函数y依赖于单个变量的情形.如果y是多个自变量x1,2,…,xm 的函数,那么可以把这些自变量本身视为一组基,建立如下模型: y≈Cx1+c2r2十·+Cmxm 来预测,其中系数{c}沿,可利用最小二乘法求解,即 店小 在数理统计中,上述方法又称为多元线性回归 例9.8为了开拓市场,某公司对其新产品作了一系列调查,他们发现这一新产品 的销量与下列事件关系密切:其一是温度,其二是上证指数,其三是广告费,其四是推 销员数,其五是返修率,详细数据见下表 记录温度上证指数广告费推销员数返修率销售量 139 567 10000 2 0.20 75 2 37 679 0 3 0.15 68 3 30 346 5000 3 0.10 105 4 25 987 5000 3 0.08 136 25 1101 0 4 0.07 152 6 10 1004 5000 5 0.07 191 7 15 667 0 4 0.05 148 8 5 604 10000 6 0.04 234 假设这些事件与销量量近似成线性关系,试求这种关系的数学表达式 解设销售量为头,用x1,x2,x3,工4,工5分别表示温度、上证指数、广告费、推销员数、 返修率,则需确定函数
9.3 最小二乘法 15 前面主要讨论了函数y 依赖于单个变量的情形. 如果y 是多个自变量 x1, x2, · · · , xm 的函数, 那么可以把这些自变量本身视为一组基, 建立如下模型: y ≈ c1x1 + c2x2 + · · · + cmxm, 来预测 y, 其中系数 {ci} m i=1 可利用最小二乘法求解, 即 min c1,c2,··· ,cm∈R ∑n j=1 [∑m i=1 cixij − yj ]2 . 在数理统计中, 上述方法又称为多元线性回归. 例 9.8 为了开拓市场, 某公司对其新产品作了一系列调查, 他们发现这一新产品 的销量与下列事件关系密切: 其一是温度, 其二是上证指数, 其三是广告费, 其四是推 销员数, 其五是返修率, 详细数据见下表. 记录 温度 上证指数 广告费 推销员数 返修率 销售量 1 39 567 10000 2 0.20 75 2 37 679 0 3 0.15 68 3 30 346 5000 3 0.10 105 4 25 987 5000 3 0.08 136 5 25 1101 0 4 0.07 152 6 10 1004 5000 5 0.07 191 7 15 667 0 4 0.05 148 8 5 604 10000 6 0.04 234 假设这些事件与销量量近似成线性关系, 试求这种关系的数学表达式. 解 设销售量为 y, 用 x1, x2, x3, x4, x5 分别表示温度、上证指数、广告费、推销员数、 返修率, 则需确定函数 y = c1x1 + c2x2 + c3x3 + c4x4 + c5x5

16 第九章函数逼近 利用最小二乘法,系数C1,C2,·,C6需要满足法方程组: 5390132881 76500059421.75 21091 13288149063372339500022886533.67 858427 765000233950002750000001350003650 5250000 594 22886 135000 124 2.46 4636 21.75 533.67 3650 2.460.0928/ C5 87.35 解得 y≈0.68772x1+0.043703x2+0.0048631x3+29.607x4-447.36x6. 接下来,讨论矛盾方程组的最小二乘解.若记 F(C1,c2,… )∑s)-/h 则F(C1c2,…,Cm)是关于变量C,c2,·,Cm的多元二次函数.令 p1(1)p2(1)… m(z1) f(x1) p1(2)p2(x2)· m(r2) f= f(x2) A= p1(xn)p2(xn)·pm(xn) f(n) Fa,c2,…,cn)=‖Ac-fl6=eTATAe-2 eTATt+fE 一般地,当n之m时,若线性方程组Ac=无解,则称它为矛盾方程组.对于矛盾方 程组,称取到 min llAe-fl2 (9.11) 的c为矛盾方程的最小二乘解容易看出,矛盾方程的最小二乘解是内积空间Rn中的 最佳平方逼近问题,即在A的列空间中选取元素最佳逼近Rn中的元素í此外,数据 拟合的最小二乘问题(9.8)可以视为矛盾方程组的最小二乘解.从前面的讨论可知,矛 盾方程的最小二乘解可通法方程组求解,即 Gc=b→ATAc=ATf
16 第九章 函数逼近 利用最小二乘法, 系数 c1, c2, · · · , c5 需要满足法方程组: 5390 132881 765000 594 21.75 132881 4906337 23395000 22886 533.67 765000 23395000 275000000 135000 3650 594 22886 135000 124 2.46 21.75 533.67 3650 2.46 0.0928 c1 c2 c3 c4 c5 = 21091 858427 5250000 4636 87.35 解得: y ≈ 0.68772x1 + 0.043703x2 + 0.0048631x3 + 29.607x4 − 447.36x5. 接下来, 讨论矛盾方程组的最小二乘解. 若记 F(c1, c2, · · · , cm) , ∑n i=1 [∑m j=1 cjφj (xi) − f(xi) ]2 , 则 F(c1, c2, · · · , cm) 是关于变量 c1, c2, · · · , cm 的多元二次函数. 令 A = φ1(x1) φ2(x1) · · · φm(x1) φ1(x2) φ2(x2) · · · φm(x2) . . . . . . . . . . . . φ1(xn) φ2(xn) · · · φm(xn) , f = f(x1) f(x2) · · · f(xn) , 则 F(c1, c2, · · · , cm) = A c − f 2 2 = c T A TAc − 2c T A T f + f T f. 一般地, 当 n ≫ m 时, 若线性方程组 A c = f 无解, 则称它为矛盾方程组. 对于矛盾方 程组, 称取到 min c∈Rm A c − f 2 2 (9.11) 的 c 为矛盾方程的最小二乘解. 容易看出, 矛盾方程的最小二乘解是内积空间 R n 中的 最佳平方逼近问题, 即在 A 的列空间中选取元素最佳逼近 R n 中的元素 f. 此外, 数据 拟合的最小二乘问题 (9.8) 可以视为矛盾方程组的最小二乘解. 从前面的讨论可知, 矛 盾方程的最小二乘解可通法方程组求解, 即 G c = b ⇐⇒ A TA c = A T f.�

93最小二乘法 17 注解9.1利用多元二次函数的极值理论,亦可导出求解矛盾方程最小二乘解的法 方程组.事实上,多元二次函数F(c1,c2,·,Cm)取极值的必要条件为 de =2ATAc-2ATf=0 ATAc=AT f 即驻点条件.又因为ATA是半正定的,所以函数F(C1,c2,·,c)在驻点取到最小值 关于矛盾方程的最小二乘解有下面的结论, 定理9.11设A∈Rn×m,f∈Rn,则 (1)线性方程组ATAx=Af恒有解: (2)函数Ax-,取到最小值←→x满足ATAx=ATE (3)线性方程组ATAx=ATf的解是唯一的一rankA=n 更多的例子 最后,利用矩阵A的秩来分析最小二乘问题解集的性质 (1)当rank(A)=m=n时,即A是可逆方阵.最小二乘问题(9.1l)与线性方程组 Ac=f同解,且解是唯一的; (2)当rank(A)=m<n时,即A是列满秩的.因为rank(ATA)=rank(A)=m,所以 ATA可逆,最小二乘问题的解也是唯一的: (3)当rank(A)<min{m,n时,即A是秩亏损的.此时,最小二乘问题有无穷多组 解 对于前两种情形,最小二乘问题的解可以通过求解线性方程组得到,常用的方法包 括:Cholesky分解、QR分解等方法.而对于最后一种情形,必须采用特殊的求解方法, 且需要考虑确定数值秩这一难题,一个常用的方法是使用奇异值分解(Singular Value Decomposition,.SVD),具体的内容可参见文献[1I]
9.3 最小二乘法 17 注解 9.1 利用多元二次函数的极值理论, 亦可导出求解矛盾方程最小二乘解的法 方程组. 事实上, 多元二次函数 F(c1, c2, · · · , cm) 取极值的必要条件为 ∂F ∂c = ∂F ∂c1 ∂F ∂c2 . . . ∂F ∂cm = 2A TAc − 2A T f = 0 ⇐⇒ A TA c = A T f, 即驻点条件. 又因为 ATA 是半正定的, 所以函数 F(c1, c2, · · · , cm) 在驻点取到最小值. 关于矛盾方程的最小二乘解有下面的结论. 定理 9.11 设 A ∈ R n×m, f ∈ R n , 则 (1) 线性方程组 ATA x = AT f 恒有解; (2) 函数 A x − f 2 取到最小值 ⇐⇒ x 满足 ATA x = AT f; (3) 线性方程组 ATA x = AT f 的解是唯一的 ⇐⇒ rank A = n. 更多的例子... 最后, 利用矩阵 A 的秩来分析最小二乘问题解集的性质: (1) 当 rank(A) = m = n 时, 即 A 是可逆方阵. 最小二乘问题 (9.11) 与线性方程组 Ac = f 同解, 且解是唯一的; (2) 当 rank(A) = m < n 时, 即 A 是列满秩的. 因为 rank(ATA) = rank(A) = m, 所以 ATA 可逆, 最小二乘问题的解也是唯一的; (3) 当 rank(A) < min {m, n} 时, 即 A 是秩亏损的. 此时, 最小二乘问题有无穷多组 解. 对于前两种情形, 最小二乘问题的解可以通过求解线性方程组得到, 常用的方法包 括: Cholesky 分解、QR 分解等方法. 而对于最后一种情形, 必须采用特殊的求解方法, 且需要考虑确定数值秩这一难题, 一个常用的方法是使用奇异值分解 (Singular Value Decomposition, SVD), 具体的内容可参见文献 [11]

18 第九章函数逼近 9.4最佳平方逼近与正交多项式 本节主要讨论函数的最佳多项式逼近问题,即连续情形的最佳平方逼近问题.记 L[a,是区间[a,上满足 厂K)PG)d<+ 的Lebesgue可积函数∫构成的函数类,其中称非负函数p(x)为权函数,如果p(x)满 足 ④)对于非负整数n积分广grd止存在且有限 ()对于非负连续函数g,若有厂pag国d正=0则gaey三0 显然,当p(x)三1时,即为L2[a,.在La,司中,定义 (f,g)=p()f(x)g()dr,vfgeL2la,b Ja f川=Vf,f),f∈a,. 不难验证,(,)与‖·‖分别构成a,b的内积与范数 令P国为所有次数不超过n的多项式构成的空间,则Pn是La,b)的n+1 维子空间.利用定理9.8知,对任意的f∈L2[a,,存在唯一的n次多项式 n). 使得∫一p川取到最小值,即最佳平方逼近多项式.多项式p(x)的系数可由如下法方 程确定: 22,e=0.,j=0,1…,n (9.12) 其中 ()=p(a)d ()=p(z)()dz. 例9.9设f(c)=sn(πx),求f(x)在区间0.1】上的二次最佳平方逼近多项式
18 第九章 函数逼近 9.4 最佳平方逼近与正交多项式 本节主要讨论函数的最佳多项式逼近问题, 即连续情形的最佳平方逼近问题. 记 L 2 ρ [a, b] 是区间 [a, b] 上满足 ∫ b a ρ(x)f 2 (x) dx < +∞ 的 Lebesgue 可积函数 f 构成的函数类, 其中称非负函数 ρ(x) 为权函数, 如果 ρ(x) 满 足: (1) 对于非负整数 n, 积分 ∫ b a ρ(x)x n dx 存在且有限; (2) 对于非负连续函数 g(x), 若有 ∫ b a ρ(x)g(x) dx = 0, 则 g(x) [a,b] ≡ 0. 显然, 当 ρ(x) ≡ 1 时, 即为 L 2 [a, b]. 在 L 2 ρ [a, b] 中, 定义 (f, g) = ∫ b a ρ(x)f(x)g(x) dx, ∀f, g ∈ L 2 ρ [a, b], ∥f∥ = √ (f, f), ∀f ∈ L 2 ρ [a, b]. 不难验证, (·, ·) 与 ∥ · ∥ 分别构成 L 2 ρ [a, b] 的内积与范数. 令 Pn[x] 为所有次数不超过 n 的多项式构成的空间, 则 Pn[x] 是 L 2 ρ [a, b] 的 n + 1 维子空间. 利用定理9.8知, 对任意的 f ∈ L 2 ρ [a, b], 存在唯一的 n 次多项式 p(x) = ∑n i=0 cix i ∈ Pn[x], 使得 ∥f − p∥ 取到最小值, 即最佳平方逼近多项式. 多项式 p(x) 的系数可由如下法方 程确定: ∑n i=0 (x j , xi ) ci = (f, xj ), j = 0, 1, · · · , n, (9.12) 其中 (x j , xi ) = ∫ b a ρ(x)x i+j dx, (f, xj ) = ∫ b a ρ(x)f(x)x j dx. 例 9.9 设 f(x) = sin(πx), 求 f(x) 在区间 [0, 1] 上的二次最佳平方逼近多项式