中国地质大学（武汉）：《信号与系统 Signals and Systems》课程教学资源（课件讲稿）第五章 拉普拉斯变换

§5.2性质 -(2)s→0，s=0+j0,δ→0,0→0（慢变信号） -(3)定理条件： SF(S)在除原点外的π，解析 ,中分u)us@不满是定理条件 17

17 §5.2 性质 – (2) – (3)定理条件： s s      0, j , 0, 0     慢变信号   r sF s  在除原点外的  解析 2 2   0 0 cos s u t t s     ，不满足定理条件

§5.3拉普拉斯逆变换 ·极点、零点： F)=L{}= N(s) -F(s)的极点p,台F(p,)=o,当N与D互素时， p,即D(s)的零点。 -F(s)的零点z,→F(z,)=0,当N与D互素时， z即W(s)的零点。 18

18 §5.3拉普拉斯逆变换 • 极点、零点： – –          N s F s f t D s   L       i i N D i F s p F p p D s 的极点   ，当 与 互素时， 即 的零点。       i i 0 N D i F s z F z z N s 的零点   ，当 与 互素时， 即 的零点

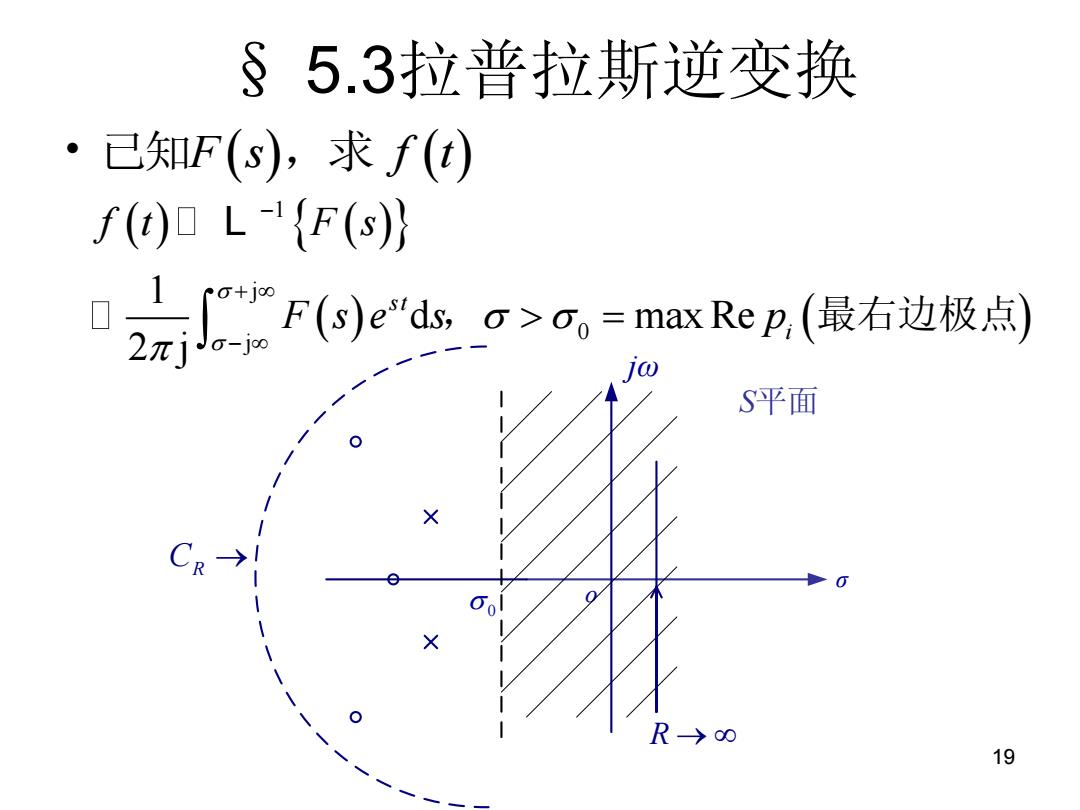
§5.3拉普拉斯逆变换 oi 知F(s),求f(t) f(LF(s) 2Fed>a,=maxRP(最右边极向司 S平面 ● C R->oo 19

19 § 5.3拉普拉斯逆变换 • 已知F s f t  ，求            1 j 0 j 1 d max Re 2 j s t i f t F s F s e s p              ， 最右边极点 L σ o jω  0 R   S平面 CR 