核心重难探究 知识点 相似多边形的概念与特征 【例题】如图,把矩形ABCD对折,折痕为MN,矩形DMNC与 矩形ABCD相似,已知AB=4. M ()求AD的长; (2)求矩形DMNC与矩形ABCD的相似比 B W C 思路点拨:(1)矩形ABCD的边AB,AD分别与矩形DMNC的哪 条边对应? 2)如何求相似比?
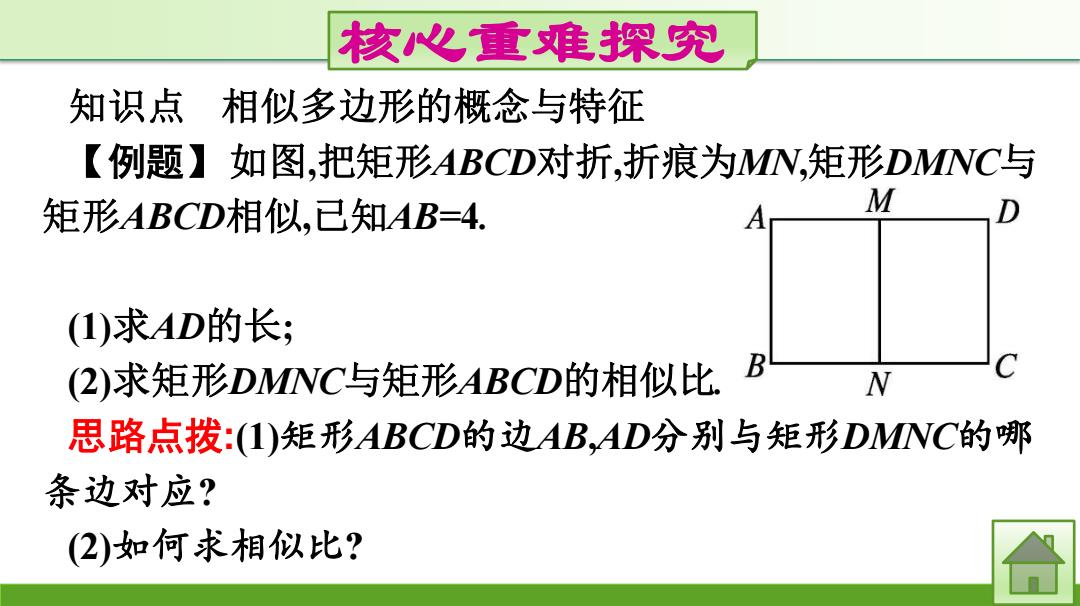
核心重难探究 知识点 相似多边形的概念与特征 【例题】如图,把矩形ABCD对折,折痕为MN,矩形DMNC与 矩形ABCD相似,已知AB=4. (1)求AD的长; (2)求矩形DMNC与矩形ABCD的相似比. 思路点拨:(1)矩形ABCD的边AB,AD分别与矩形DMNC的哪 条边对应? (2)如何求相似比?

解:()由己知,得MIN=AB-=4,MD-AD. .'矩形DNC与矩形ABCD相似, ·DM MN DC AB BC 又MIN=DC ∴2AD2=16,AD=4V2. (2)矩形DMNC与矩形ABCD的相似比为 DM = 2V2 = AB 4 2 合
解:(1)由已知,得 MN=AB=4,MD=𝟏 𝟐 AD. ∵矩形 DMNC 与矩形 ABCD 相似, ∴ 𝐃𝐌 𝐀𝐁 = 𝐌𝐍 𝐁𝐂 = 𝐃𝐂 𝐀𝐃 ,又 MN=DC, ∴ 𝟏 𝟐 AD2 =16,∴AD=4 𝟐. (2)矩形 DMNC 与矩形 ABCD 的相似比为 𝐃𝐌 𝐀𝐁 = 𝟐 𝟐 𝟒 = 𝟐 𝟐