
家庭猴伞 第1课时 相以三角形对应线段比的性质
第1课时 相似三角形对应线段比的性质

基础自主梳理 导 核心重难探究 航 新知川练巩固 素能演练提升
导 航 基础自主梳理 核心重难探究 新知训练巩固 素能演练提升

基础自住梳理 1.相似三角形的性质定理 相似三角形对应高的比、对应角平分线的比、对应中线的 比都等于 名师指导 掌握该性质,一定要注意相似比的顺序性以及线段的对应问 题,这个性质为我们今后证明线段成比例提供了重要依据
基础自主梳理 1.相似三角形的性质定理 相似三角形对应高的比、对应角平分线的比、对应中线的 比都等于相似比 . 名师指导 掌握该性质,一定要注意相似比的顺序性以及线段的对应问 题,这个性质为我们今后证明线段成比例提供了重要依据

2.已知△4BCn△DEF,若△4BC与△DEF的相似比为 则△ABC与△DEF对应中线的比为(A). 4 A. 3 16 1 D 9 3.如果两个相似三角形对应高的比为3·2,那么这两个 相似三角形对应角平分线的比为(A), A.3.2 B.9.4 C.V3:V2 D.34
2.已知△ABC∽△DEF,若△ABC 与△DEF 的相似比为𝟑 𝟒 , 则△ABC 与△DEF 对应中线的比为( ). A. 𝟑 𝟒 B. 𝟒 𝟑 C. 𝟗 𝟏𝟔 D. 𝟏𝟔 𝟗 3.如果两个相似三角形对应高的比为 3∶2,那么这两个 相似三角形对应角平分线的比为( ). A.3∶2 B.9∶4 C. 𝟑 ∶ 𝟐 D.3∶4 A A
核心重难探究 知识点 相似三角形对应线段比的性质 【例题】如图,△ABC是一张锐角三角形的硬纸片,AD是边 BC上的高,BC=40cm,AD=30cm.从这张硬纸片上剪下一个长 HG是宽HE2倍的矩形EFGH.使它的一边EF在BC上,顶点 G,H分别在AC,AB上.AD与HG的交点为M, (求证 AM HG H M G (2)求矩形EFGH的周长. B E D F (
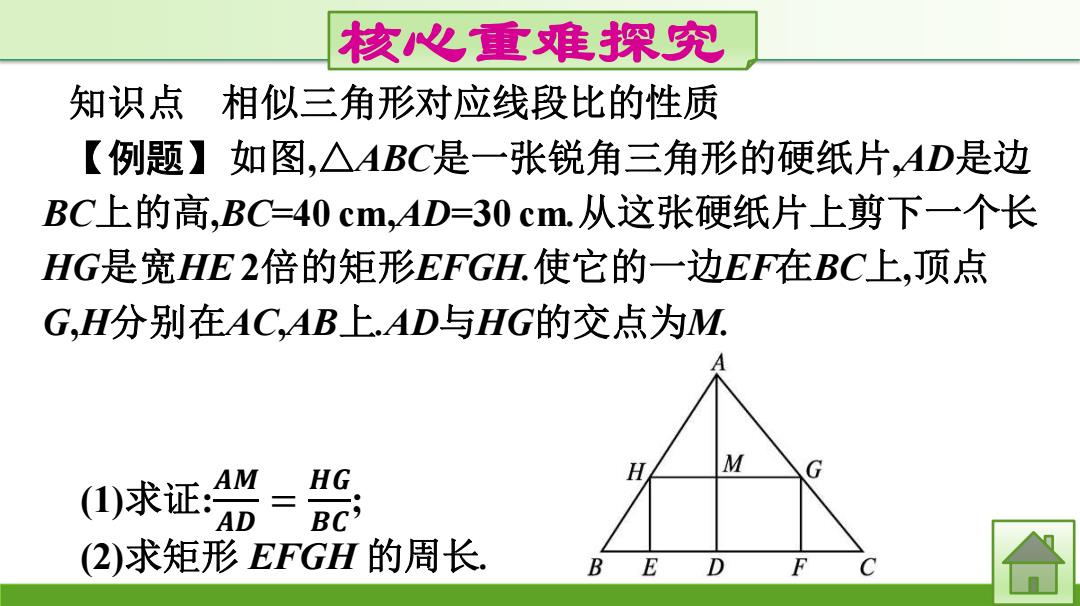
核心重难探究 知识点 相似三角形对应线段比的性质 【例题】如图,△ABC是一张锐角三角形的硬纸片,AD是边 BC上的高,BC=40 cm,AD=30 cm.从这张硬纸片上剪下一个长 HG是宽HE 2倍的矩形EFGH.使它的一边EF在BC上,顶点 G,H分别在AC,AB上.AD与HG的交点为M. (1)求证: 𝑨𝑴 𝑨𝑫 = 𝑯𝑮 𝑩𝑪 ; (2)求矩形 EFGH 的周长