例:电感电路 (t1) 新稳定 L Us 状态等 效电路 S未动作前,电路处于 稳定状态:i=0,w红=0。 R 新的稳 S接通电源后很长时 定状态 间,电路达到新的稳定 uL 状态,电感视为短路: 前一个稳 0有一个1 uL =0,i= Us 定状态 过渡期 R 2019/10/18 6
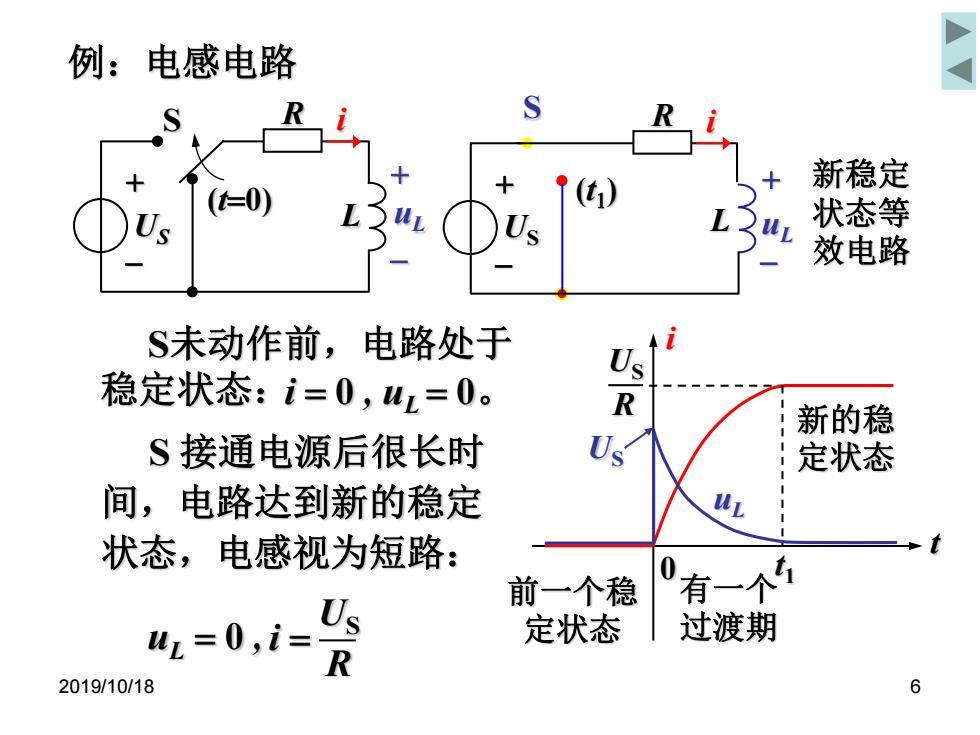
2019/10/18 6 例:电感电路 uL i US + - + - S R L (t1 ) S 接通电源后很长时 间,电路达到新的稳定 状态,电感视为短路: S未动作前,电路处于 稳定状态: uL 0 , i 0 , uL 0。 有一个 过渡期 0 t i R US 前一个稳 定状态 US 新的稳 定状态 t1 uL uL i US + - + - S R (t0) L US R 新稳定 状态等 效电路 i

产生暂态过程的必要条件: ()电路中含有储能元件(内因) (2)电路发生换路(外因) 若Wc发生突变 换路:电路状态的改变。如: 则i=C duc 电路接通、切断、短路、电压 di 产生暂态过程的原因: 般电路不可能! 由于物体所具有的能量不能跃变而浩成 在换路瞬间储能元件的能量也不能饮变 C储能:1 uc不能突变 1 L储能: WL- L说 2 .i不能突变 2019/10/18 7
2019/10/18 7 产生暂态过程的必要条件: L储能: 2 2 1 WL L iL 换路: 电路状态的改变。如: 电路接通、切断、 短路、电压改变或参数改变 C 储能: \ uC 不能突变 2 2 1 WC C uC 产生暂态过程的原因: 由于物体所具有的能量不能跃变而造成 在换路瞬间储能元件的能量也不能跃变 若 u c 发生突变, d t d u i C C C 一般电路不可能! 则 (1) 电路中含有储能元件 (内因) (2) 电路发生换路 (外因) \ i L 不能突变

3.1.2换路定则 设:仁0一表示换路瞬间(定为计时起点) =O一表示换路前的终了瞬间(旧电路,稳态) =0+一表示换路后的初始瞬间(新电路,暂态) 仁0一表示换路后很长时间(新电路,稳态值) 电感电路:i(0+)=iz(0_) 电容电路:wc(0+)=uc(0_) 注:换路定则仅用于换路瞬间来确定 暂态过程中uc、i初始值。 2019/10/18 8
2019/10/18 8 电容电路: ( 0 ) ( 0 ) u C + u C - 注:换路定则仅用于换路瞬间来确定 暂态过程中 uC、 iL初始值。 设:t=0 — 表示换路瞬间 (定为计时起点) t=0-— 表示换路前的终了瞬间(旧电路,稳态) t=0+—表示换路后的初始瞬间(新电路,暂态) t=∞—表示换路后很长时间(新电路,稳态值) 3.1.2 换路定则 电感电路: ( 0 ) ( 0 ) L + L -

3.1.3初始值的确定 初始值:电路中各、i在t=0,时的数值。 求解要点: (1)uc(0+)、iz(0+)的求法。 1)先由t=0.的电路求出wc(0_)、z(0_): 2)根据换路定律求出uc(0+)、z(0+)。 (2)其它物理量初始值的求法。 由t=0,的电路求其它电量的初始值; 2019/10/18 9
2019/10/18 9 3.1.3 初始值的确定 求解要点: (2)其它物理量初始值的求法。 初始值:电路中各 u、i 在 t =0+ 时的数值。 (1) uC ( 0+ )、iL ( 0+ ) 的求法。 1) 先由t =0-的电路求出 uC ( 0– ) 、iL ( 0– ); 2) 根据换路定律求出 uC ( 0+ )、iL ( 0+ ) 。 由t =0+的电路求其它电量的初始值;
例1.暂态过程初始值的确定 已知:换路前电路处稳态, C、L均未储能。 试求:电路中各电压和电 流的初始值。 (a) 解:(由换路前电路求4c(0_),i(0_) 由已知条件知uc(0)=0,i(0)=0 根据换路定则得:4c(0,)=uc(0)=0 i(0+)=i(0.)=0 2019/10/18 10
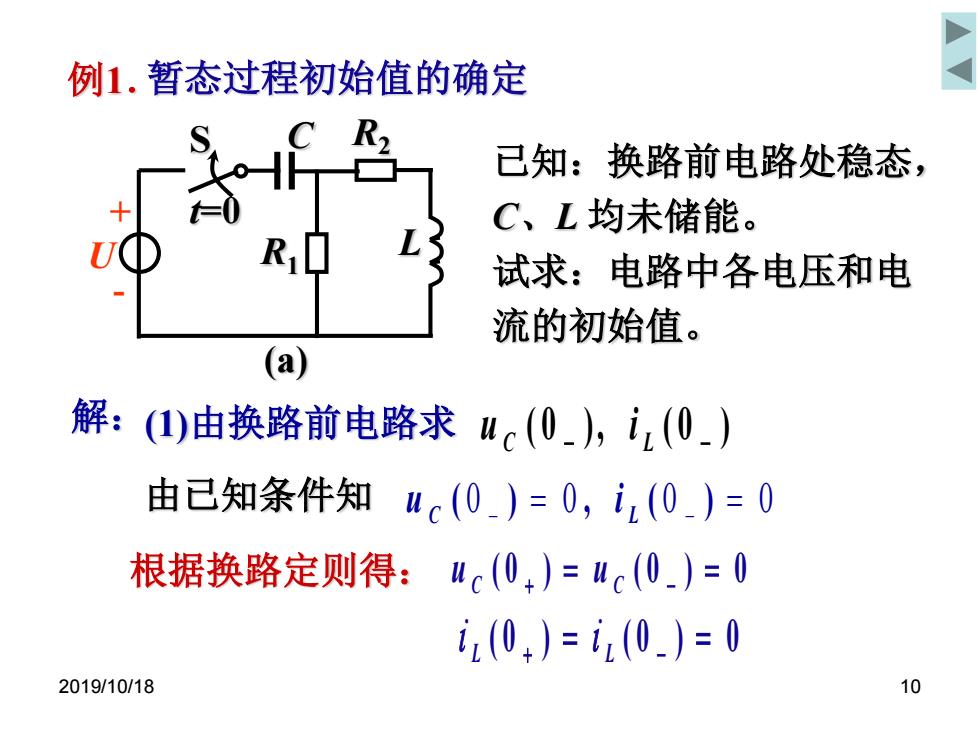
2019/10/18 10 例1.暂态过程初始值的确定 解:(1)由换路前电路求 ( 0 ) , ( 0 ) C - L - u i 由已知条件知 0 0 0 0 - - ( ) , ( ) C L u i 根据换路定则得: ( 0 ) ( 0 ) 0 C + C - u u ( 0 ) ( 0 ) 0 L + L - 已知:换路前电路处稳态, C、L 均未储能。 试求:电路中各电压和电 流的初始值。 S C R2 (a) U R1 + t=0 - L