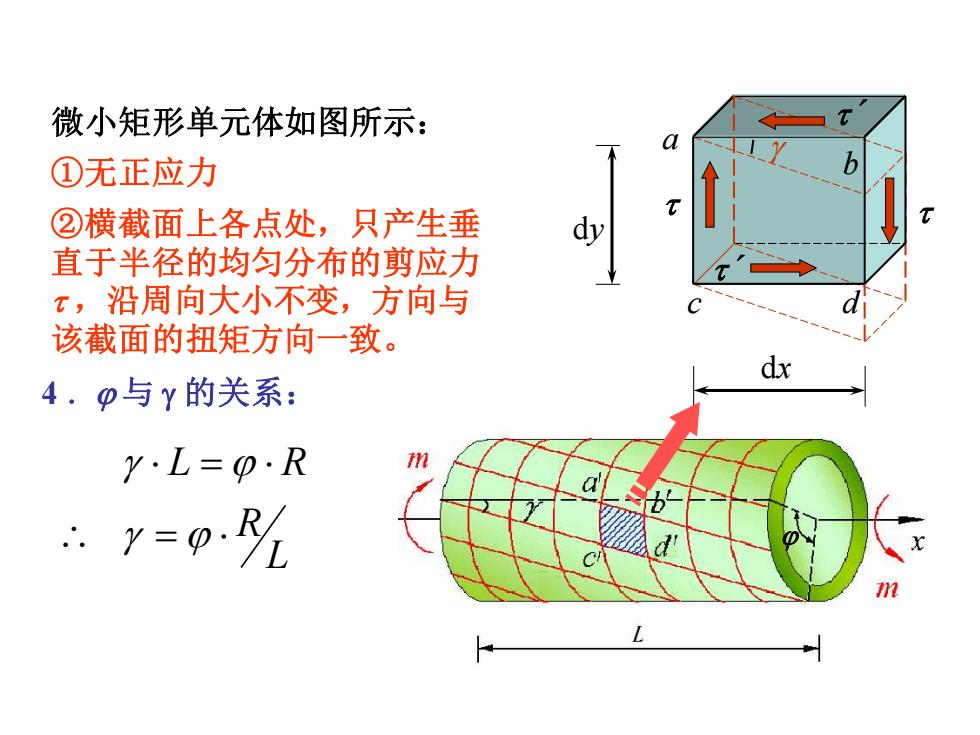
微小矩形单元体如图所示: ①无正应力 ②横截面上各点处,只产生垂 直于半径的均匀分布的剪应力 x,沿周向大小不变,方向与 该截面的扭矩方向一致。 dx 4.p与y的关系: Y·L=p·R n .y=o% d
a c d dx b dy ´ ´ ①无正应力 ②横截面上各点处,只产生垂 直于半径的均匀分布的剪应力 ,沿周向大小不变,方向与 该截面的扭矩方向一致。 4 . 与 的关系: L R L R = = 微小矩形单元体如图所示:
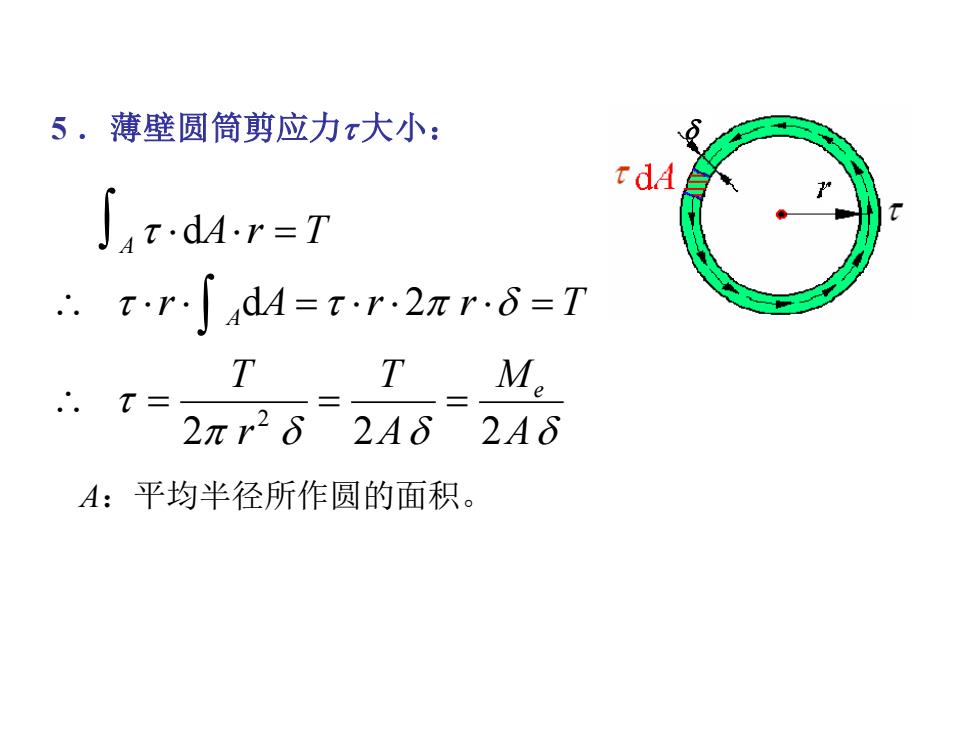
5.薄壁圆筒剪应力x大小: ∫4d4r=T .TrdM=tr2πr6=T T T M 2πr26 2A62A6 A:平均半径所作圆的面积
5 .薄壁圆筒剪应力大小: 2 2 2 d 2 d 2 A M A T rT r A r r T A r T e A A = = = = = = A:平均半径所作圆的面积。
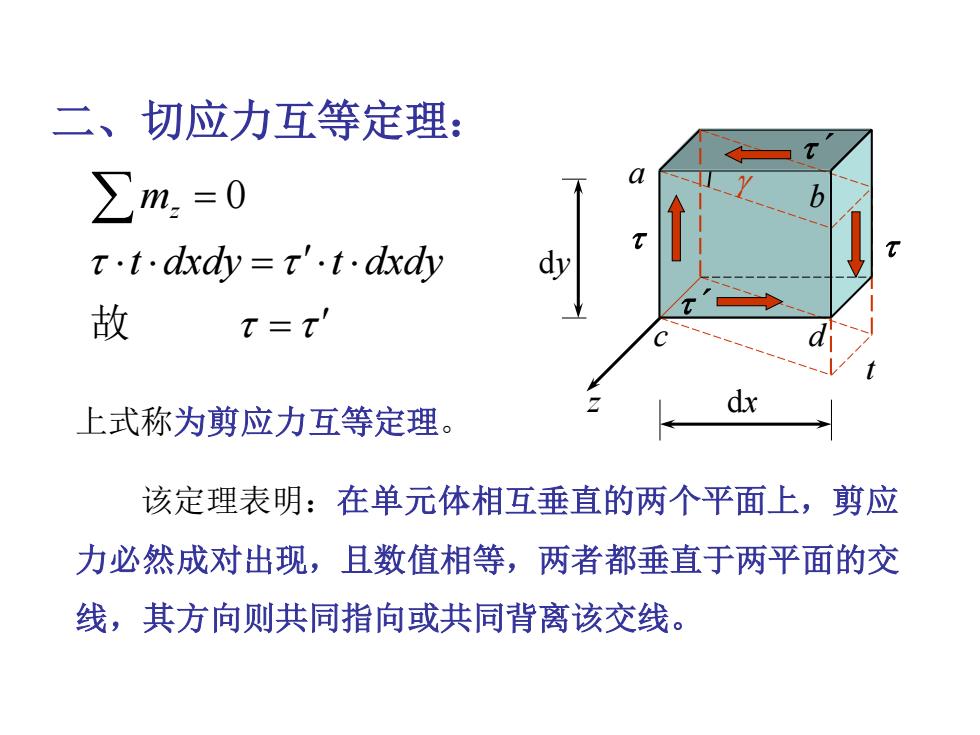
二、切应力互等定理: ∑m.=0 t·t.dxdy=t'.t.dxdy 故 T=T dx 上式称为剪应力互等定理。 该定理表明:在单元体相互垂直的两个平面上,剪应 力必然成对出现,且数值相等,两者都垂直于两平面的交 线,其方向则共同指向或共同背离该交线
二、切应力互等定理: = = = 0 故 t dxdy t dxdy mz 上式称为剪应力互等定理。 该定理表明:在单元体相互垂直的两个平面上,剪应 力必然成对出现,且数值相等,两者都垂直于两平面的交 线,其方向则共同指向或共同背离该交线。 a c d dx b dy ´ ´ t z
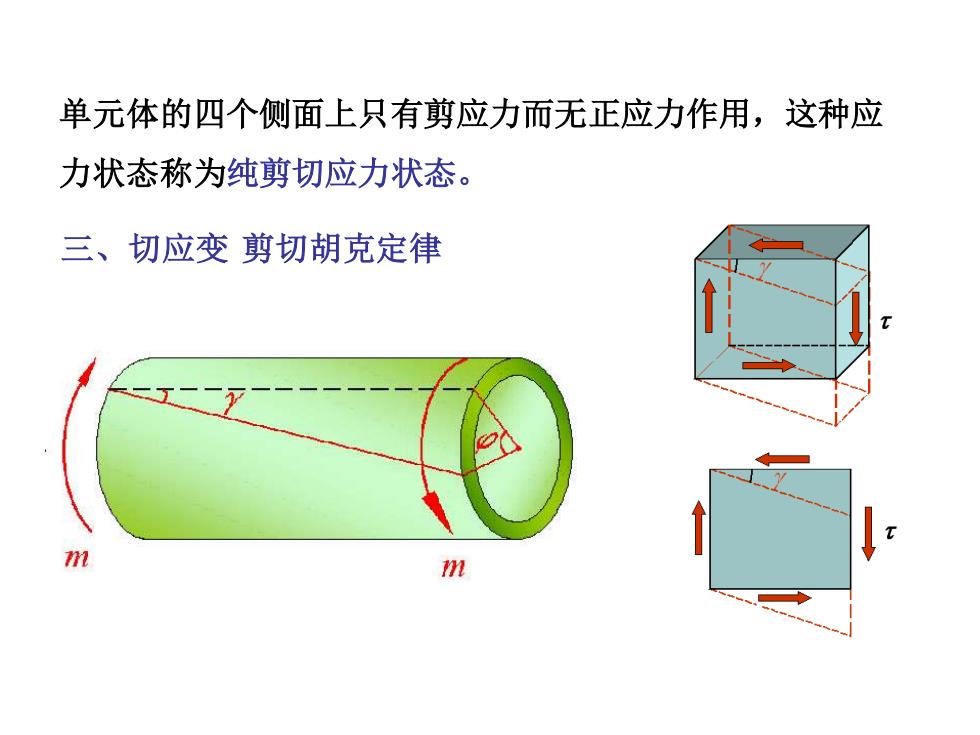
单元体的四个侧面上只有剪应力而无正应力作用,这种应 力状态称为纯剪切应力状态。 三、切应变剪切胡克定律 71 m
三、切应变 剪切胡克定律 单元体的四个侧面上只有剪应力而无正应力作用,这种应 力状态称为纯剪切应力状态
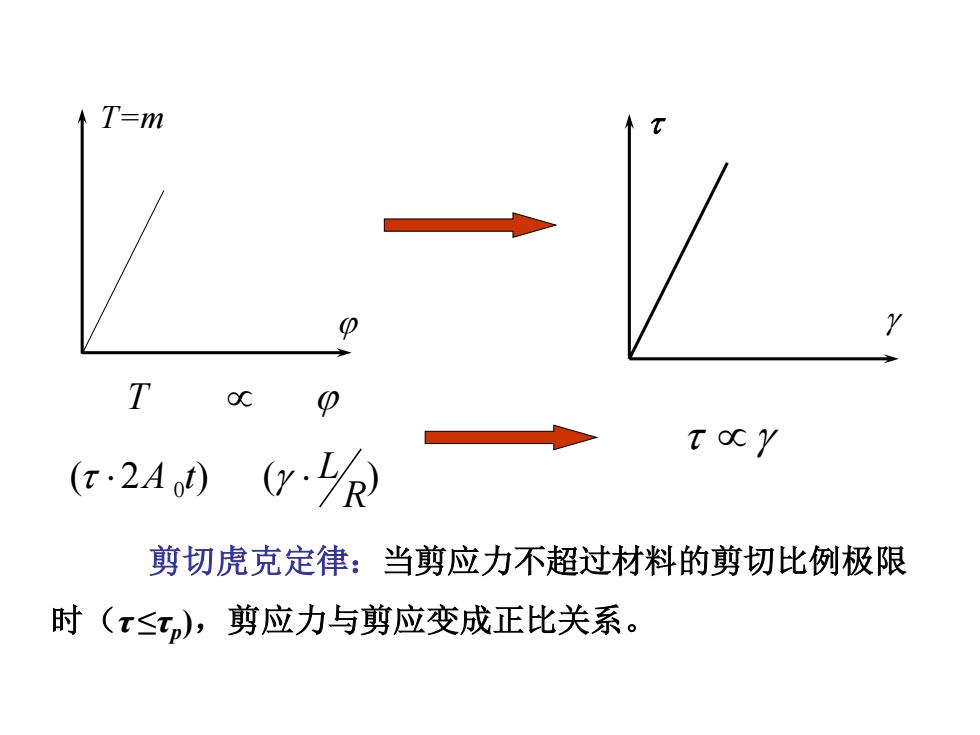
T=m T t ocy (r2A0)(0y.) 剪切虎克定律:当剪应力不超过材料的剪切比例极限 时(x≤,),剪应力与剪应变成正比关系
T=m ( 2 ) ( ) 0 R A t L T 剪切虎克定律:当剪应力不超过材料的剪切比例极限 时(τ ≤τp ),剪应力与剪应变成正比关系