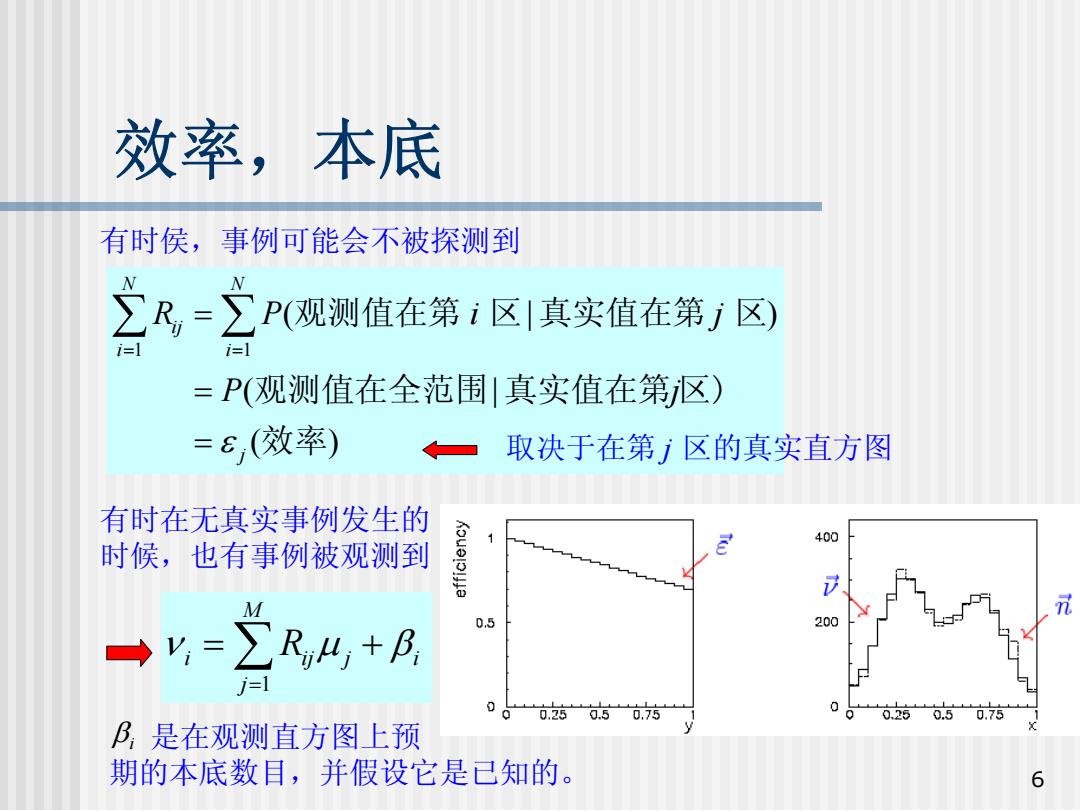
效率,本底 有时侯,事例可能会不被探测到 立R,=立P(观测值在第i区真实值在第/区 i=l P(观测值在全范围!真实值在第区) =6,(效率) 取决于在第j区的真实直方图 有时在无真实事例发生的 400 时候,也有事例被观测到 M 0.5 =∑R,4+B i=1 0 00.250.50.75 0 0.25 0.5 0.75 B是在观测直方图上预 期的本底数目,并假设它是已知的。 6
6 效率,本底 有时侯,事例可能会不被探测到 是在观测直方图上预 期的本底数目,并假设它是已知的。 有时在无真实事例发生的 时候,也有事例被观测到 1 1 ( | ) ( | ( ) N N ij i i j R P i j P j ε = = = = = ∑ ∑ 观测值在第 区 真实值在第 区 观测值在全范围 真实值在第 区) 效率 ∑= = + M j i Rij j i 1 ν μ β βi 取决于在第 j 区的真实直方图

各关键量总汇 M 真实"直方图:=(4,,4M) 4o=∑4 M个区间 i=1 概率:p=(P1,pM)=i/4o 观测直方图的期待值:=(y1,,VN) N个区间 观测直方图:n=(n,,nw) 反应矩阵:R=P(观测值在第i区|真实值在第j区) 效率:6,=∑R 预期的本底:B=(B,Bx) i= ETn]==Rii+B 为了找到u的估计量,需要相关的概率理论,例如:P(,;y) 上 n 泊松分布,或关联矩阵V,=Cov[n,n,]以便构造logL或X
7 各关键量总汇 “真实 ”直方图: 观测直方图的期待值: 反应矩阵: 效率: ∑= = = M j M tot j 1 1 μ ( μ ,..., μ ), μ μ 概率: 观测直方图: G M tot p ( p1,..., p ) μ / μ G G = = ( ,..., ) ν = ν 1 ν N G ( ,..., ) 1 N n = n n G ( | ) R P ij = 观测值在第 i 区 真实值在第 j 区 ∑= = N i j Rij 1 ε ( ,..., ) 预期的本底: β = β1 β N G ν μ β G G G G E [ n ] = = R + 为了找到 的估计量,需要相关的概率理论,例如: i i e n P n i n i i i ν ν ν − = ! ( ; ) 泊松分布,或关联矩阵 Vij = cov[ ni , n j ] 以便构造 2 log L 或 χ μ G M个区间 N个区间

为什么要用开拆法 般而言,我们并不需要开拆法,例如当比较现有理论的预期值时,最好 是将探测器相应叠加到理论中去。即在预期值中包含探测器效应并与未修 正的原始数据n相比较。 但是,不将实验数据进行开拆处理,结果发表后,有关反应矩阵的知识将 不在保留。而且,开拆后的分布可以直接与各种理论的预言相比较,也可 以与别的实验经过开拆以后的分布相比较。 通常开拆的结果更为有用,因为当反应矩阵变得不可恢复时,即使对实验 结果可能又有了新的理论解释,也很难进行理论检验。 在粒子物理研究中,开拆法常用的领域为: ·结构函数 ●τ的谱函数(也就是强子不变质量谱) ·强子事例形状分布 ·粒子多重数分布 8
8 为什么要用开拆法 一般而言,我们并不需要开拆法,例如当比较现有理论的预期值时,最好 是将探测器相应叠加到理论中去。即在预期值中包含探测器效应并与未修 正的原始数据 相比较。 但是,不将实验数据进行开拆处理,结果发表后,有关反应矩阵的知识将 不在保留。而且,开拆后的分布可以直接与各种理论的预言相比较,也可 以与别的实验经过开拆以后的分布相比较。 n G 通常开拆的结果更为有用,因为当反应矩阵变得不可恢复时,即使对实验 结果可能又有了新的理论解释,也很难进行理论检验。 在粒子物理研究中,开拆法常用的领域为: •结构函数 • τ 的谱函数 (也就是强子不变质量谱 ) •强子事例形状分布 •粒子多重数分布 •...
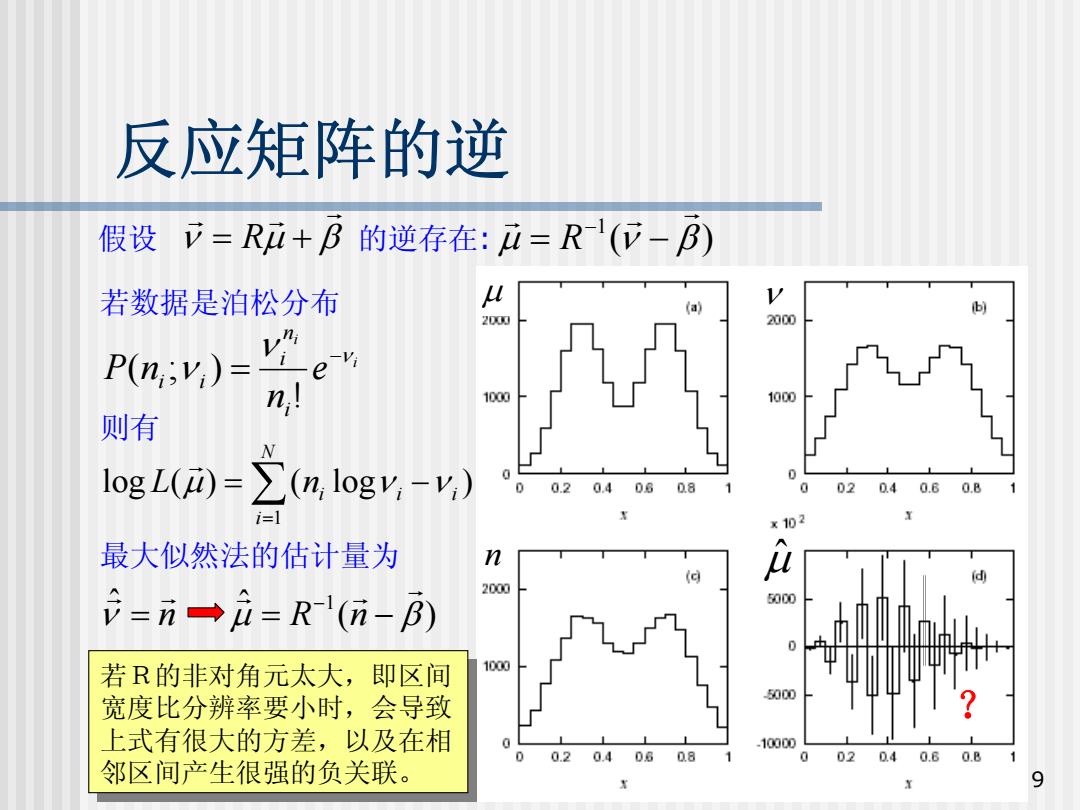
反应矩阵的逆 假设 立=Ri+B的逆存在:i=R(位-B) 若数据是泊松分布 V a 6 200 2000 P(n;y,)= -e n n 1000 1000 则有 l1ogL(0)=∑(n,logy,-y) 04 0608 02040.60.B i=l x102 最大似然法的估计量为 n u 2000 =n→ǜ=R(m-B) 5000 若R的非对角元太大,即区间 1000 5000 宽度比分辨率要小时,会导致 上式有很大的方差,以及在相 -10000 0. 0.4 0 0.8 0 02 040.6 0.B 邻区间产生很强的负关联。 9
9 反应矩阵的逆 假设 的逆存在: 若数据是泊松分布 μ β 最大似然法的估计量为 ν G G G = R + ( ) 1 μ ν β G G G = − − R i i e n P n i n i i i ν ν ν − = ! ( ; ) ∑= = − N i i i i L n 1 log ( μ) ( log ν ν ) G ( ) ˆ ˆ 1 ν μ β G G G G G = = − − n R n 则有 μ ν n μˆ 若R的非对角元太大,即区间 宽度比分辨率要小时,会导致 上式有很大的方差,以及在相 邻区间产生很强的负关联。 若R的非对角元太大,即区间 宽度比分辨率要小时,会导致 上式有很大的方差,以及在相 邻区间产生很强的负关联。 ?