
3.使用泰勒公式 以此方法为基础,有龙格-库塔法、线性多步法等方 法. 4.数值公式的精度 当一个数值公式的截断误差可表示为O(h+1)(其 中k为正整数,为步长)时,称它是一个阶公式: 越大,则数值公式的精度越高. ·欧拉法是一阶公式,改进的欧拉法是二阶公式, ·龙格-库塔法有二阶公式和四阶公式. 线性多步法有四阶亚当斯外插公式和内插公式, 返回
3.使用泰勒公式 以此方法为基础,有龙格-库塔法、线性多步法等方 法. 4.数值公式的精度 当一个数值公式的截断误差可表示为O(h k+1)(其 中k为正整数,h为步长)时,称它是一个k阶公式. k越大,则数值公式的精度越高. •欧拉法是一阶公式,改进的欧拉法是二阶公式. •龙格-库塔法有二阶公式和四阶公式. •线性多步法有四阶亚当斯外插公式和内插公式. 返 回
(三)用MATLAB软件求常微分方程的数值解 [t,x]-solver('f',ts,x0,options) ode45 ode23 自变 数 由待解 ts=[t0,t 函数 ode11 3ode1 方程写 f],t0、 的初 量值 值 5sode 成的M tf为自变 值 23s 文件名 量的初值 和终值 ode23:组合的2/3阶龙格-库塔-费尔贝格算法 ode45:运用组合的4/5阶龙格-库塔-费尔贝格算法 用于设定误差限(缺省时设定相对误差103,绝对误差10-6), 命令为:options=odeset('reltol',rt,'abstol',at), rt,at:分别为设定的相对误差和绝对误差
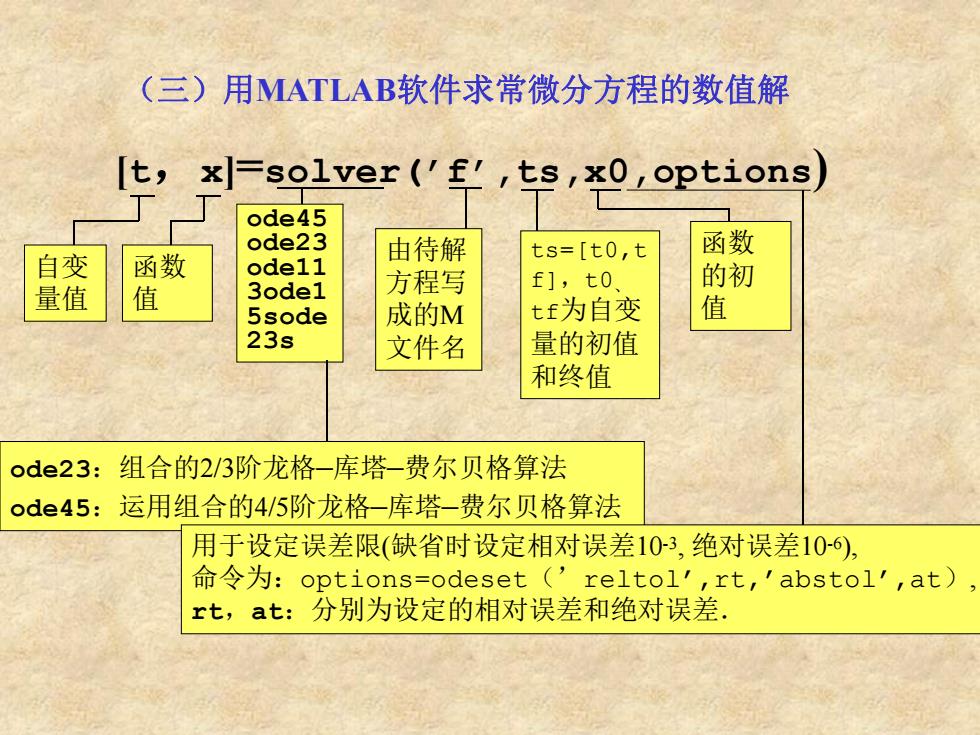
(三)用MATLAB软件求常微分方程的数值解 [t,x]=solver(’f’ ,ts,x0,options) ode45 ode23 ode11 3ode1 5sode 23s 由待解 方程写 成的M 文件名 ts=[t0,t f],t0、 tf为自变 量的初值 和终值 函数 的初 值 ode23:组合的2/3阶龙格–库塔–费尔贝格算法 ode45:运用组合的4/5阶龙格–库塔–费尔贝格算法 自变 量值 函数 值 用于设定误差限(缺省时设定相对误差10-3 , 绝对误差10-6), 命令为:options=odeset(’ reltol’ ,rt, ’abstol’ ,at), rt,at:分别为设定的相对误差和绝对误差.