
至于参考点的选择,一般情形是任意的。参考点不同,各点的电位都增加(或减小)一个常数。由电的定义Vae -{"E.dl-f'E.dl+f"E.dlI'E.d]-E.dl-@-@(1. 35)电压也就是两点的电位差。然而,电压却与参考点的选择无关。当取E沿闭合路径的线积分时,如图1.18所示,有图1.18E沿闭合路径的积分SE.dl-E·dl +E.dlE.dl-1E.dl1amAVAB-VAR-O(1.36)一个矢量沿一个闭合路径的线积分称为这个尖量的环流(环量)。静电场的环流为零,这是静电场是位场的表现。从作功的观点来看,此环流等于沿闭合路径移动单位正电荷时电场力所作之功。上式指出,当试验电荷回到出发点时电场所作的净功为零,即电场无能量变化,静电场的这个性质也称为保守性。当电分布已知时,可以求出场中任一点的电位。对于点电荷,如取距离为Rp的点为参考点,则rnpq_"rdRTRPE.dl-9cp=J, Axecrar dl=AEoJR R?JRIf:y4oA4+C(1. 37)4REORIRATEUR4TEoRP4mEnR其中C=一q/4πeRp,与参考点的选择有关,如令Rp=,则C=0。对于体、面、线电荷,电位为:120

pdt体电荷:ΦC(1.38),AREpRosdsΦ+0(1. 69).面电荷:·Ea.dlΦ --(1. 40)线电荷:4enR其中R是由源点到场点的距离。例1.5求均勾分布于一个半径为α的圆盘上的电荷在与圆盘垂直的轴线上一点的电位。电荷密度为ps库/米2(图1.19)。解:取一个宽度为、半径为T的圆环,出于dr很小,源点到场图1.19带均勺面电荷的圆盘点的距离即为V22+r,圆环在点的电位为ps2ardrd:AneVz? +?整个圆盘在“点的电位为rdrDs9Φ=+c..V22a-1+02e0JnV2 +r2ZE如令z=,Φ=0,即选择无限远作参考点,则s2+a-2@=260l顺便指山,在无限大面电荷情形(上式中α=情形),如选择无限远作参考点,则Φ变为无限大。对于无限长线电荷也有类似情形。对于.上述两种情形,参考点只能在有限远处选择。所以,只有当电荷分布于有限空间中的情形下,才能选择无限远作参考点。电场中电位相同的点所构成的面称为等位面。例如点电荷的等位面是以点电荷为心的球面。等位面和电力线之间有一个重要的关系,即等位面与电力线是互相垂直的。这是因为在一个等位.21
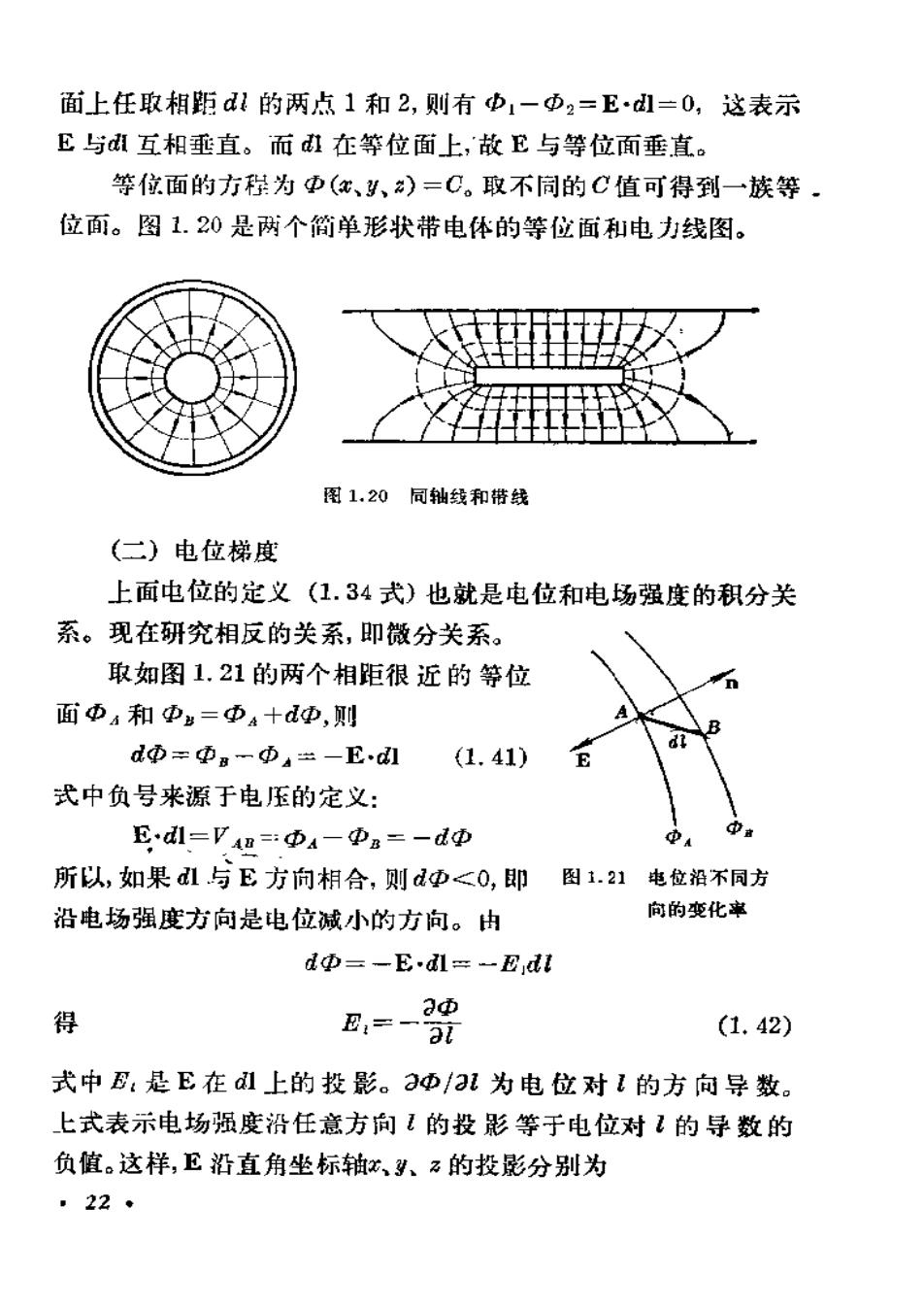
面上任取相距dl的两点1和2,则有Φ1-Φ2=E·dl=0,这表示E与dl互相垂直。而d在等位面上,故E与等位面垂直。等位面的方程为@(a、y、2)=C。取不同的C值可得到一族等。位面。图1.20是两个简单形状带电体的等位面和电力线图。图1.20同轴线和带线(二)电位梯度上面电位的定义(1.34式)也就是电位和电场强度的积分关系。现在研究相反的关系,即微分关系。取如图1.21的两个相距很近的等位面和=则--E.dl(1.41)式中负号来源于电压的定义:E-dl-Van=@-@--dp办所以,如果al与E方向相合,则d@<o,即图1.21电位措不同方向的变化率沿电场强度方向是电位减小的方向。由d@--E-dl- -EdtE,=-20得(1. 42)al式中E:是E在dl上的投影。ad/al为电位对1的方向导数。上式表示电场强度沿任意方向1的投影等于电位对1的导数的负值。这样,E沿直角坐标轴、3、z的投影分别为.22

abadaF=.a,EyE.+aaoy'可得2d+a.ga)a+a0E=a,E,+a,E,-a,E,=-(a.utau用一个符号grad@表示括弧中的欠量,称为电位梯度。即p+aaadgrad @ =a.c(1. 43)a2z则E=-grad@(1. 44)所以,电位梯度足和E大小相等,方向相反的一个矢量。我们来看一下梯度的意义。设n为等位面的法线矢量(n沿Φ增加的方向),则grad@和E分别与n平行和反平行;梯度在n上的投影等于E在n上的投影的负值。即adgrad,b=-E, m(1. 45)此亦即梯度的模。而Φ/3%是Φ沿等位面的法线方向的变化率很明显,电位沿法线方向变化最快;2Φ/2n为最大变化率,所以梯度的模等于电位的最大变化率。梯度的方向为电位增加最快的方向。电位梯度在直角坐标系的表达式即(1.43)式。利用矢量算符V,电位梯度可以表为VΦ,故(1.44)式可以写成E=-V(1. 46)在圆柱坐标系和球坐标系中,VΦ的表达式分别为迎+a一+1+a.Vo=a,or(1. 47)ad1 ad及Vo=argr(1. 48)+a.+asin·23

1.6旋度静电场的无旋性上节中研究了静电场的矢虽沿闭合路径的线积分的性质。矢量沿一个闭合路径的线积分称为矢量的环流。它也是矢量场的性质的一个量度方法.在流体中。如果某处有漩涡存在,则有流体沿闭合路径流动,而流速欠量沿闭合路径的环流将不等于零。仿此。在任何矢量场中,如果失量的环流不等于零,我们也可以想象为有某种物体沿闭合路径流动。因而在该处即有产生此种流动的原因,即“旋涡源”存在。场中每点旋涡源的强度是矢量场在每点性质的一个量度。我们以某一矢量场A为例。为了研究场中某点的性质,取包含此点的一个面元AS,沿着包围这个面元的闭合路径取A的线积分。令AS→0,取如下的极限f,A-dllim"As此极限具有单位面积的环流的意义。但是,我们立即可以看出,比值Φ,A·dl/A.s与所取而元的方向有关。例如在流体情形,某点流体沿着一个面上呈漩涡状流动时,如果我们取的面元和漩涡的面相舍,则积分中,A·αl为最大值;如取的面元和漩涡面之间有一个角度,积分总是小于此最大值;面当面元和漩涡面相垂直时,积分等于零。同样,在矢量A的场中,我们也可以找到一个面元,此面元上环流A·dl为最大值。面元取其它方向时,积分不过是此最大值在此面元上的投影。为了计算上述的极限值,我们把而元看作一个失量△S,它的方向为面元的法线的正方向n,且n与·24