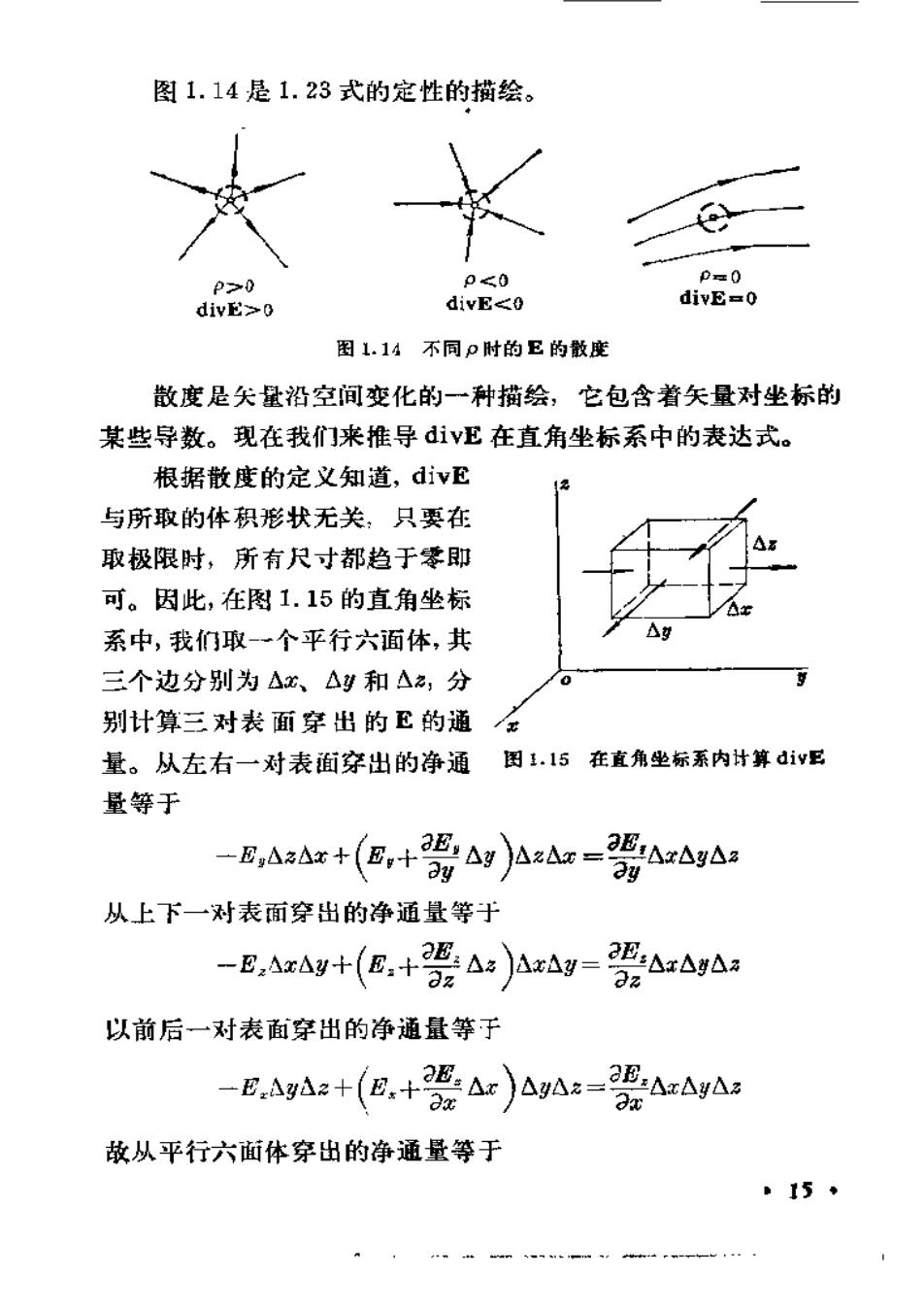
图1.14是1.23式的定性的描绘。paop<0p0divE-0divE<0divE>0图1.14不同p时的E的散度散度是尖量沿空间变化的一种描绘,它包含着矢量对坐标的某些导数。现在我们来推导divE在直角坐标系中的表达式。根据散度的定义知道,divE与所取的体积形状无关,只要在取极限时,所有尺寸都趋于零即可。因此,在图1.15的直角坐标系中,我们取一个平行六面体,其三个边分别为△、y和A,分别计算三对表面穿出的E的通图1.15在直角坐标系内计算divE量。从左右一对表面穿出的净通量等于+aE Ng )AzAa=-1Aag-E,Aa#+(E,+y从上下一对表面穿出的净通量等于-E,AAy+(E + A )AAy =EAaaz以前后一对表面穿出的净通量等于aEiArs-Ag2+(B.+-A)AyAa=aaaa故从平行六面体穿出的净通量等于15

(+ +)ArAyAs+ E-ds=(faz+ay+(2E +3E +2.)AT令AT-→0.则$ E-ds2+21+2imf+Ar得到E的散度为divE -+ 2F++2E.(1.24)+ey+o3a可见散度由场矢量的空间导数纽成;它是E在各坐标轴上的投影沿各自坐标的变化率之和。我们规定一个矢最算子√,称为"del"算子(或称“纳布拉”算子),定义为aO(1. 25)V=azO则divE可以用V和E的标量积表示,因为V·E=(a,.(aE+aE,+aE)a2aun2E11OECE.divE(1.26)aru22在圆柱坐标系和球坐标系中,divE的展开式分别为:圆柱坐标div E%(rE)++(1.27)rar球坐标aE111%(E,)+adivE%++sin%(sin 0E0)+rsino(1.28)对于圆柱坐标、球坐标和其它坐标,divE也用V·E表示。16

因为divE等于从单位体积发出的E的通量,所以从体积发出的E的通量等于divE的体积分WV·Edt这个通量也就是从包围的闭合面穿出的通量。所以Φ E.dsW= V.Edt=(1. 29)(1.29)式即数学中的高斯定理,也称散度定理。这个定理以后经常用到。1.5电位电位梯度(一)电位静电场的另一个重要性质是,它是一个位场。利用这个性质我们可以引入一个标量电位函数,将电场强度矢量用电位梯度表示。这样,把一个欠量场间题化为一个标量场问题。位场性质也就是电场强度久欠量的无旋性。这两节里我们将较详细地讨论这个性质。静电场的这个性质是和电场力对电荷作功有关。我们从电场力作功的概念出发来分析。当电荷o在电场中从A点沿路径c移至B点时(图1.16),电场力要作功。位移为dl时,电场力作功为dA-F-dl-Fdl cos 0-qpEdl cos 9(1.30)当<元/2时,dA>0,为电场力推动9.运动而作功,电场消耗了能量;当6元/2时dA0,为外力反对电场力推动qo运动而作功,电场获得能量。沿路径所作之功为A-I, F.dl -qoJ,E.dl=4 Ed cos ?(1.31).17:

图1.10电场力对电荷作功图1.179.在点电荷场中运动时作的动为了分析作功的性质,首先研究试验电荷90在一个点电荷9的电场中运动时电场力所作之功(图1.17)。在路径上一点P,40移动l时,电场力作功为dA-E-dl-ARd由图可见ar-dl=dl cosd :=dR故沿某一路径c从A到B时电场力作功为A-4of E-dl - Jo4 dR49[1AnEJR,R?ATEolR991L(1. 32)4元ELRAR.其中R是A与4的距离,R是B与的距离。(1.32)式表示一个重要的事实,邸在点电荷的电场中,电荷9从A沿某一路径℃移至B点时,电场作的功仅与始点和终点的位置有关,而与路径无关。换言之,沿不同路径移动时,只要始点和终点位置不变,作的功都是相同的。对于有N个点电荷的电场情形,试验电荷40沿某一路径c由A到B时电场力作的功为.18

J-d=[md+ d1=++aTo.I [dRiaR .. dR]4zLRiRR[g(R-R)1)+42(R2-R2)14x611+a(RR)1=2()410可见在N个点电荷的场中,试验电荷运动时电场力所作之功同样仅与起点和终点位置有关,而与路径无关。由点电荷的电场得到的结论不难推广到体电荷、面电荷和线电荷的电场,因为这些分布电荷划分成很小的单元时,每个单元电荷即相当一个点电荷,所以,它们的电场也必然具有上述点电荷的场的性质。换言之,上述结论是所有静电场的一个共性。取A与4a的比值,即电场对单位正电荷所作之功,用Vaa表示,称为AB两点间的电压,单位为伏。-A-( E·alVAn=α=](1.33)因为此功只和始点和终点的位置有关,如果我们取一个定点P作为终点,则作功为起点坐标的函数,称为电位,用@表示,而固定的终点则为计算电位的参考点。A点的电位记为apprE.dlE-dl-P=(1.34)(HA*梦A'Z)故电位是点的坐标(、9、2)的函数。对于一给定的电场,当参考点选定后,其各点的电位有完全确定的值;而参考点的电位即为零。·19