
角(图1.9)可以这样来计算:取dS在以。为心、半径R的球面上的投影dS·a与R的比值,即为面元对o点所张的立体角。ds图1.9任查面元dS在0点的立体角do-ds.arB.-dScos 6(1. 15)R2R2其中r是径向的单位失量。同样可见,这个立体角是与所取的计算球面的半径无关的。一个任意形状的闭合面对一点0所张的立体角有两种情形:一种是。在闭合面内,可以用点为心作一球面,则闭合面上任-面无&S对。点所张的立体角也就是它对0点所构成的锥体在球面上割出的一块球面元的立体角。可见,整个闭合面对。点所张的立体角和球面对。点的立体角是相等的。所以,任意闭合面对福(a)闭合面对面内的(6)闭合而对面外的点。的立体角点0的立体角图1.10闭合面的立体角·10

面内一点的立体角是4元球面度。另一种情形是点。在闭合面外(图1.10%),不难看出,所张的立体角是零,因为闭合面的两部分表面的立体角等值异号之故。现在来证明高斯定理。先研究一个点电荷的情形。电场强度E沿一个面元as的通量为qdS cos ?qar'dsE-ds=-(1.16)R2AnEOR24元E0上式中最后的分式就是&s对点所张的立体角dQ。因此,E沿一个闭合面的通量为f ds cos d.92-$a?$ E.ds --24元OJS4neoJ京上式最后一个积分是闭合面对点电荷所张的立体角。当闭合面包围点电荷时,由于闭合面对面内一点所张的立体角为4,上式变为$ E·ds=1-4n =1(1.17)4EE0当点电荷位于闭合面之外时,则由于闭合面对点电荷所张的立体角为零,故通量为零。即当闭合面内的电量为零时,从面内穿出的通量也为零。如果闭合面内有N个点电荷41、42、,里x,卿从面内穿出的通量等于各电荷的通量的代数和。即+ E.ds- + Etds+ +, E ds+.-Ey.ds+-g-.9 + +.(1.18)门EEO上式可推广到体电荷、面电荷和线电荷情形。对于所有情形:Z表示闭合面8内的总电荷。对于一般情形,在给定电荷分布时高斯定理不能直接用来计11

算电场强度,因为高斯定理只给出E沿一个闭合面的通量,而由此通量的值一般无法求出面上任一点的E。但是,当电荷按一定的对称性分布时,我们可以选择这样一个闭合面(高斯面),面上各点E的值相同且与面垂直(或者在一部分表面上与表面平行),则在此情形,(1.14)式变为f Eds=E4 ds =ES-29E0用高斯定理计算无可由面内的净电量求出E。下面举例说图1.11限长直线电荷的E明其应用。例1.2求线电荷密度为p:库/米的无限长直导线的电场。解:可以看出,此电场具有轴对称性,即E只有?方向的分量,且在以导线为轴的圆柱面上E的值是相同的,即E与9、2无关。因此、取如图1.11中的圆柱形闭合面,计算从闭合面内穿出的通量。因为E与上下两底面平行,没有通量穿过此两底面,故从闭合面内穿出的E的通量为bE.ds-Eds-: ESt =E×2nrl= pl!E0因此得E-2元E0r与例1.1的结果相符合,但计算过程要简单得多。例1.3计算平板电容器的电场。设两极板上电量为及一4,极板面积为S,极板距离为d,极板间介质为空气(图1.12)。解:因为电容器极板问距离远小于极板的长度和宽度,故除*12
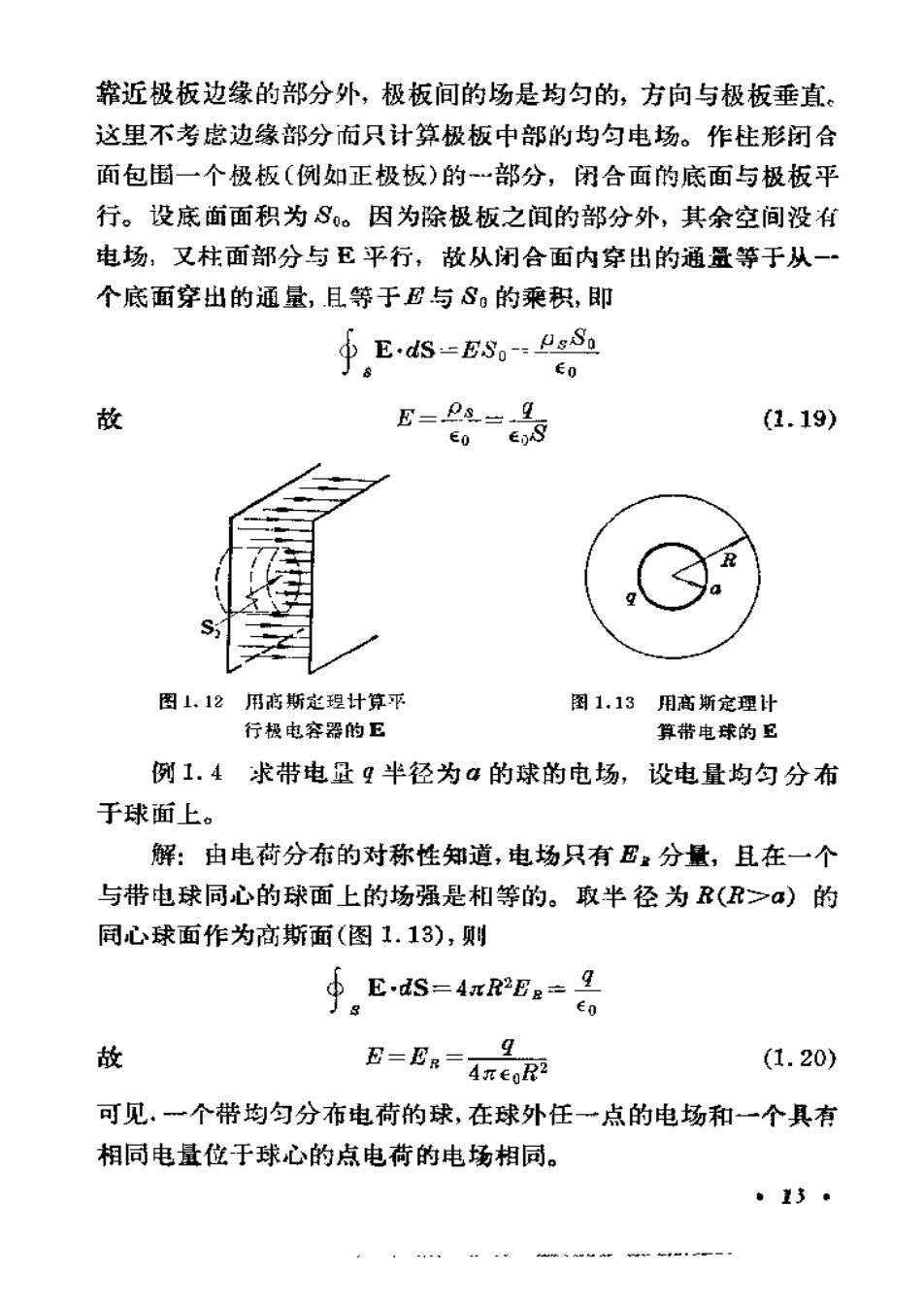
靠近极板边缘的部分外,极板间的场是均匀的,方向与极板垂直。这里不考虑边缘部分而只计算极板中部的均匀电场。作柱形闭合面包围一个极板(例如正极板)的部分,闭合面的底面与极板平行。设底面面积为S。。因为除极板之间的部分外,其余空间没有电场,又柱面部分与E平行,故从闭合面内穿出的通量等于从一个底面穿出的通量,且等于与S。的乘积,即+ E.ds-ES.--PsS.EOE=0s=.l.故(1.19)EOSE0图1.12用商斯定理计算平图1.13用高斯定理计行极电容器的E算带电球的E例1.4求带电量9半径为α的球的电场,设电量均勾分布于球面上。解:由电荷分布的对称性郑道,电场只有E分量,且在一个与带电球同心的球面上的场强是和等的。取半径为R(R≥a)的同心球面作为高斯面(图1.13),则5 E-dS-4RE-1eaJS故E=ER=AreoR?(1. 20)可见。个带均匀分布电荷的球,在球外任一点的电场和一个具有相同电量位于球心的点电荷的电场相同。.13

1.4电场强度E的散度上面说过,通量可以想象为某种流量;从闭合面内穿出的通量可以想象为从面内流出的某种流量。当此通量不等于零时,即有流量流出,说明闭合面内必有流量的“源”,高斯定理也就是流量和源之间的关系的反映。但是高斯定理的积分形式表示的是一个大范围的关系。场的分析要求知道场在每点上的这种关系,因为只有点的关系才能反映出场沿空间坐标的变化规律。为了确定一个点附近的电场特性,我们把闭合面收小,使包含这个点在内的体积△趋近于零,取下列极限$.E.dslimAt此极限称为矢量E在该点的散度,记为divE,即d E.as(1.21)divE limAt散度表示该点的通量密度,它是一个标量,单位为伏/米。把高斯定理应用于此小闭合面,则得$.E.asEg/10(1, 22)limlimArAtEo方程左边即E的散度,右边为电荷密度p与εo的比值。即divE=P(1. 23)to此即高斯定理的微分形式。它把每点E的散度与该点的电荷密度联系起来,是静电场中的一个基本的关系。14