
(1.76)4r-3ATEOT-1TE/%>E.92<0P(a,3,2)dyo图1.4体电荷的电场图1.3N个点电荷的合成电场即N个点源的合成电场等于各点源的电场强度的失量和。如果电荷分布于一个体积t内,其密度为p=limAg/△t(库/米?)(图1.4)),我们将体积分成体积元,当体积元At很小时,体积元的电荷Aq=pAr可以视为点电荷。根据场和点源之间的线性关系,任意场点P的电场强度等于各体积元在该点的电场强度的矢量和。*个体积元在P点的电场强度按点源公式(1.5)计算,而体积内全部电荷在P点的电场强度E等于1f p(a',y'a')ardtEx(1.8)4RER2注意,积分是求矢量和,R和都是源点(、9、)的函数如果电荷分布于-个面S上,其密度为p:=limAg/△S,则运用和上面相似的处理方法可得场点P的电场强度为[ ps(a'sy',z)E=Aredlsards(1.9)R如果电荷分布于一条线1上,其密度为p:=limAg/Al,则场点P的电场强度为1f pi(a's2andlE=(1.10)AnenJ,R2
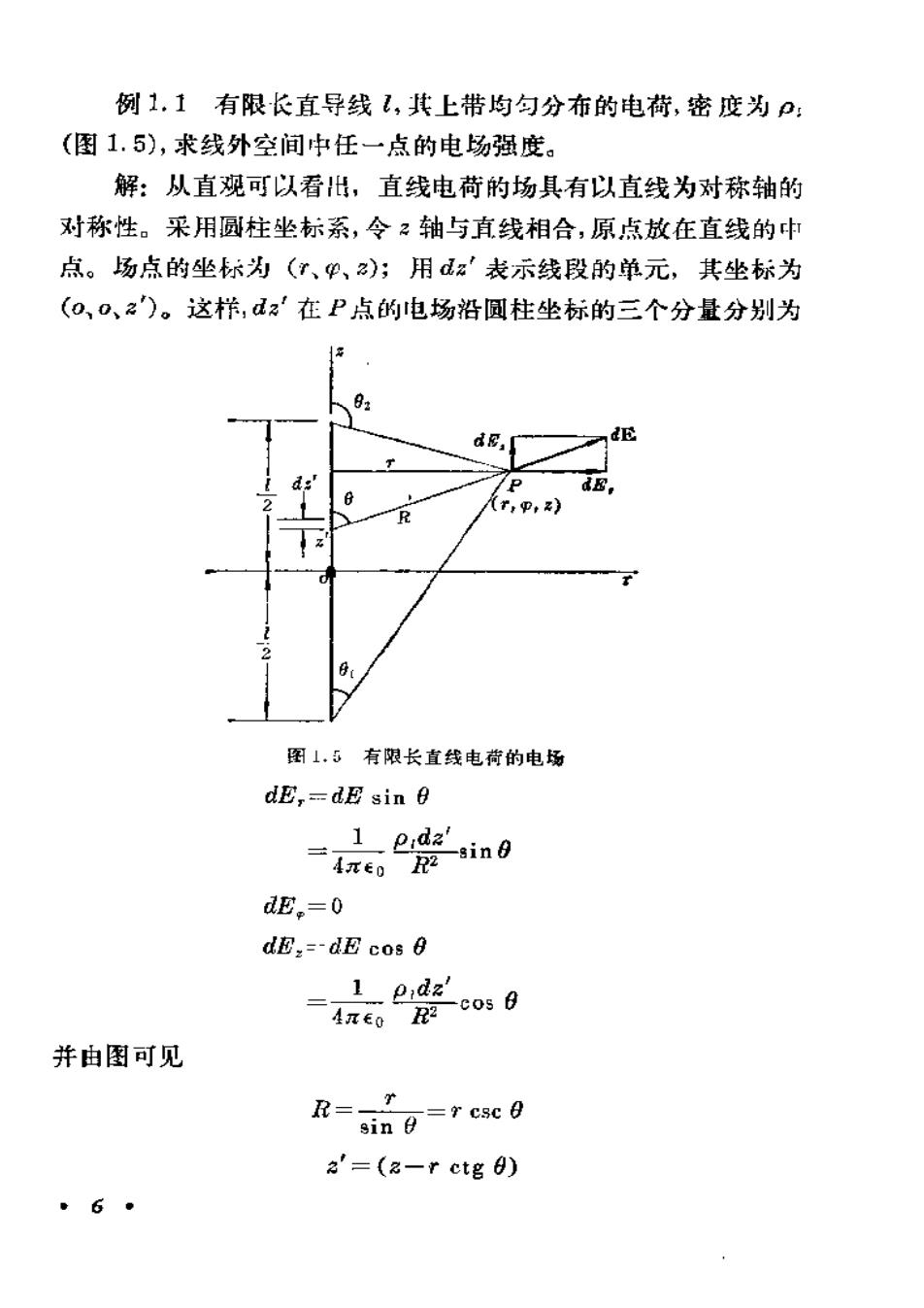
例1.1有限长直导线1,其上带均勾分布的电荷,密度为p(图1.5),求线外空间中任一点的电场强度。解:从直观可以看出,直线电荷的场具有以直线为对称轴的对称性。采用圆柱坐标系,令?轴与直线相合,原点放在直线的中点。场点的坐标为(7、甲、2);用dz表示线段的单元,其坐标为(o0、z")。这样,dz"在P点的电场沿圆柱坐标的三个分量分别为h82吃dEd:87图1.5有限长直线电荷的电场dE,-dE sin e1 pidasing4元eoR2dE.=0dE,--dE cos 8.pidzcos0AREO并由图可见R-rcscosin2'=(2-r ctg 0)6
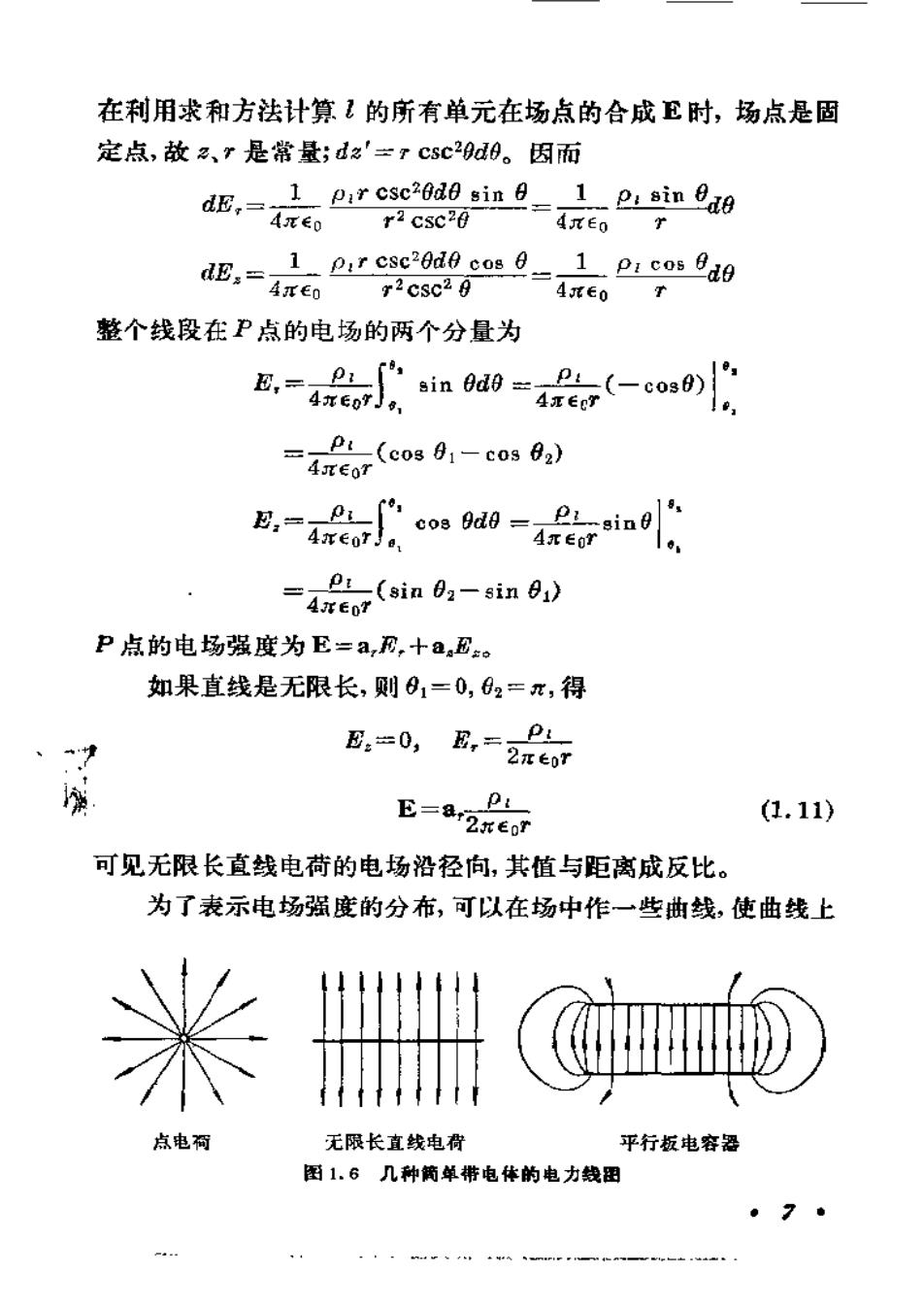
在利用求和方法计算1的所有单元在场点的合成E时,场点是固定点,故2、是常量;dz'=csc20d9。因而I Pir csc2odo gin e1 p: sin Oa8dE,:4元EOr2csc204EOX1. pir csc2odf cos 01picos BagdE,-72csc294元604mEoT整个线段在P点的电场的两个分量为01sin Ode -Ecos0)4TEr4E(cog 01-cos 02)4JTEnPrE.-cos Od -sing4tenr!4TE6-(sin 02-sin1)AEOYP点的电场强度为E=a,E,+a.Es。如果直线是无限长,则61=0,02=元,得piE,=0, E,=72元eorpE=a,(1.11)ar2nEor可见无限长直线电荷的电场沿径向,其值与距离成反比。为了表示电场强度的分布,可以在场中作一些曲线,使曲线上点电荷无限长直线电荷平行板电容器图1.6几种简单带电体的电力线图

每点的切线和该点的E的方向相同,并使线的密度(垂直于E的单位表面上的线数)正比于该点E的大小,这些曲线称为电力线。图1.6表示几种简单的带电体的电力线图。1.3高斯定理静电场是一个欠量场,人们从长期的实践发现对于一个矢量场,如果从失量沿闭合面的通量和矢量沿闭合路径的环量两方面去研究它,则可得到关于这个矢量场的基本性质的结论。本节研究电场强度失量沿闭合面的通量的性质。在电场中取一个面元AS,因为面元在空间可能有不同的取向,所以它是一个欠量。我们取它的个法线方向作为正法线方向,这就是面元的方向。用AS表示面元失量,则电场强度失量沿这个面元的通量为AW-E.AS-EAS cOs 0(1. 12)其中6是面元矢量AS与该点E之间的夹角(图1.7)。通量是一个标量。E的通量的单位为伏·米。通量的概念最初是从流体场来的。流体中各点流速不同,因面流速V是一个矢量。VAS表示穿过面元△S的流量。对于E的通量,我们也可以想象为穿过面元AS的“流量”,尽管在静电场中并没有任何物质的流动。图1.7在电场中的一个面元E沿场中任~+曲面的通量为Ye-E.ds-Ecos oas(1. 13)它等于S的各面元上的通量的代数和。如果S是一封闭的曲面,.B

则W.=Φ E·ds-pE cos ods对于闭合面,取面元AS的外法线作为正法线。因此,沿闭合面的通量是指从闭合面内穿出的通量。静电场的个重要性质是:在真空中,E沿闭合面的通量恒等于闭合面所包围的电量与真空电容率的比值。即$ E-ds=(1.14)E0其中Z4为闭合面包围的体积内的电量的代数和。从(1.14)式可见,当闭合面包围的净电量为正时,通量为正,即有净通量穿出闭合面;当闭合面包围的净电量为负时,通量为负,即有净通量穿进闭合面;面当闭合面包围的净电量为零时,从闭合面穿出的通量和进人闭合面的通量相等。(1.14)式称为真空中的高斯定理。在证明这个定理以前,首先介绍立体角的概念。在一个半径为R的球而上任取一个面元ds,则用此面元可构成一个以球心为顶点的锥体,如图1.8所示。取as与R的比值,定义为ds对球心所张的立体角,用Q表示,单位为球面度。立体角是图中的锥体的空间角度。整个球面对球心的立体角为4元R/R2=4元球面图1.8球面上的一个面元对度。由图可见,这个锥体的立体球心的立体角角并不随计算时所取球面的半径而变。如我们另取一个半径为R的球面,则此锥体在这个新的球面上割出的而元&S'与R的比值仍等于比值dS/R。一个面元&S不是球面的一部分时,它对一点o所张的立体