
2.1逻辑代数 例2.1.7 化简逻辑函数: L=AB+AC+BC+CB+BD+DB+ADE(F+G) 解:L=ABC+BC+CB+BD+DB+ADE(F+G)(利用反演律) =A+BC+CB+BD+DB+ADE(F+G) (利用A+AB=A+B) =A+BC+CB+BD+DB(利用A+AB=A) =A+BC(D+D)+CB+BD+DB(C+C) (配项法) =A+BCD+BCD+CB+BD+DBC+DBC =A+BCD+CB+BD+DBC (利用A+AB=A) =A+CD(B+B)+CB+BD =A+CD+CB+BD(利用 A+A=1) 机电学院电气工程系 上一页下一页 回目录 退出
机电学院电气工程系 上一页 下一页 回目录 退出 例2.1.7 化简逻辑函数: L = AB + AC + BC + CB + BD + DB + ADE(F + G) 解: L = ABC + BC + CB + BD + DB + ADE(F + G) (利用反演律) = A+ BC + CB + BD + DB + ADE(F + G) (利用 A + AB = A + B ) = A+ BC + CB + BD + DB (利用A+AB=A) = A+ BC(D + D) + CB + BD + DB(C + C) (配项法) = A+ BCD + BC D + CB + BD + DBC + DBC = A+ BC D + CB + BD + DBC (利用A+AB=A) = A+ CD(B + B) + CB + BD = A+ C D + CB + BD (利用 A + A = 1 ) 2.1逻辑代数

2.1逻辑代数 代数化简法的优点: 不受变量数目的限制。 缺点: 没有固定的步骤可循;需要熟练运用各 种公式和定理;需要一定的技巧和经验;不易 判定化简结果是否最简。 少机电学院电气工程系 上一页下一页回目绿 退出
机电学院电气工程系 上一页 下一页 回目录 退出 代数化简法的优点: 不受变量数目的限制。 2.1逻辑代数 缺点: 没有固定的步骤可循;需要熟练运用各 种公式和定理;需要一定的技巧和经验;不易 判定化简结果是否最简
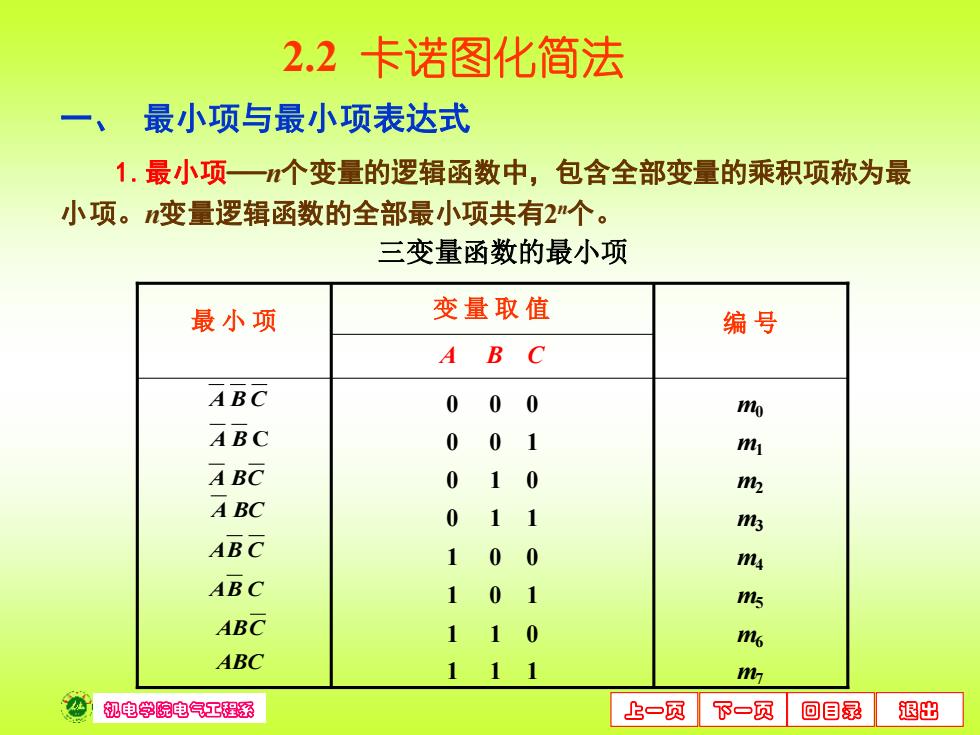
2.2卡诺图化简法 一、最小项与最小项表达式 1.最小项一个变量的逻辑函数中,包含全部变量的乘积项称为最 小项。变量逻辑函数的全部最小项共有2”个。 三变量函数的最小项 最小项 变量取值 编号 ABC 000 o ABC 001 m ABC 010 m ABC 011 % ABC 100 ma ABC 101 ms ABC 110 m ABC 111 m 心祝电学院电气工程繇 上一页 下一页 回目录 退出
机电学院电气工程系 上一页 下一页 回目录 退出 2.2 卡诺图化简法 A B C 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 变 量 取 值 最 小 项 m0 m1 m2 m3 m4 m5 m6 m7 编 号 A B C A BC A B C A BC AB C AB C ABC ABC 三变量函数的最小项 一、 最小项与最小项表达式 1.最小项——n个变量的逻辑函数中,包含全部变量的乘积项称为最 小项。n变量逻辑函数的全部最小项共有2 n个
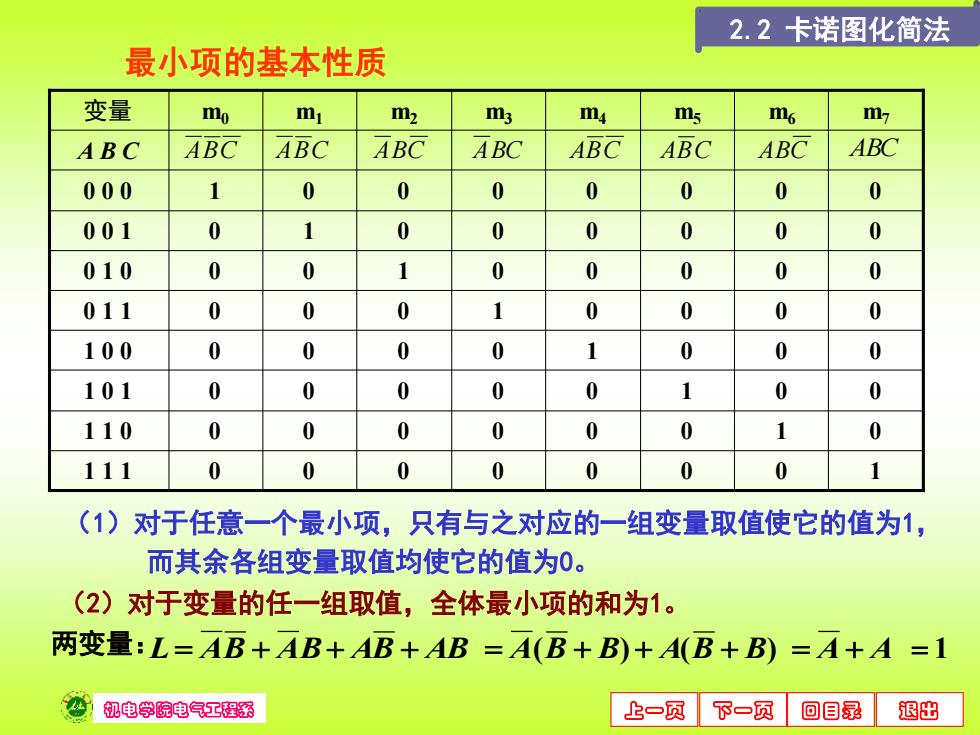
2.2卡诺图化简法 最小项的基本性质 变量 mo mi m2 m3 m4 5 mo m7 ABC ABC ABC ABC ABC ABC ABC ABC ABC 000 1 0 0 0 0 0 0 001 0 1 0 0 0 0 0 0 010 0 0 1 0 0 0 0 0 011 0 0 0 1 0 0 0 0 100 0 0 0 0 1 0 0 0 101 0 0 0 0 0 1 0 0 110 0 0 0 0 0 0 1 111 0 0 0 0 0 0 0 (1)对于任意一个最小项,只有与之对应的一组变量取值使它的值为1, 而其余各组变量取值均使它的值为0。 (2)对于变量的任一组取值,全体最小项的和为1。 两变量:L=AB+AB+AB+AB=A(B+B)+AB+B)=A+A=1 机电令院电气工程深 上一页下一页回目录退出
机电学院电气工程系 上一页 下一页 回目录 退出 最小项的基本性质 1 1 1 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 1 0 1 0 1 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 1 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 A B C 变量 m0 m1 m2 m3 m4 m5 m6 m7 ABC ABC ABC ABC ABC ABC ABC ABC (1)对于任意一个最小项,只有与之对应的一组变量取值使它的值为1, 而其余各组变量取值均使它的值为0。 两变量: L= AB + AB+ AB + AB = A(B + B) + A(B + B) = A + A = 1 (2)对于变量的任一组取值,全体最小项的和为1。 2.2 卡诺图化简法

2.2卡诺图化简法 2.逻辑函数的最小项表达式 最小项表达式一与或式中的每一个与项均为最小项。 L =ABC+ABC+ABC+ABC 任一逻辑函数可以展开为最小项表达式。 例:L=AC+AB+BC =AC(B+B)+AB(C+C)+BC(A+A) =ABC+ABC+ABC+ABC+AC+ABC =ABC+ABC+ABCABC =m+m3+mo+m =∑m(1,3,6,7) 饥电学院电气工狂深 上一页下一页 回目绿 退出
机电学院电气工程系 上一页 下一页 回目录 退出 最小项表达式——与或式中的每一个与项均为最小项。 L = ABC + ABC + ABC + ABC 任一逻辑函数可以展开为最小项表达式。 例: L = AC + AB + BC = AC(B+ B)+ AB(C +C) + BC(A+ A) = ABC + ABC + ABC + ABC + ABC + ABC = ABC + ABC + ABC + ABC = m1 + m3 + m6 + m7 = m(1,3,6,7) 2. 逻辑函数的最小项表达式 2.2 卡诺图化简法