
数字电子技术Digital Electronics Technology 第二章分析与设计数字电路的工具 名何子大学《数字电子技木》裸程组 电 活:0993-2057237 电子邮精:rl mac@shzu.edu.cn 机电学院电气工程系 上一页下一页 回目录 退出
机电学院电气工程系 上一页 下一页 回目录 退出 第二章 分析与设计数字电路的工具 数字电子技术Digital Electronics Technology 石河子大学《数字电子技术》课程组 电 话:0993-2057237 电子邮箱:rl_mac@shzu.edu.cn

2.1逻辑代数 Σ 2.2卡诺图化简法 2.3VHDL硬件描述语言基础 心机电学院电气工程系 上-页下一页回目绿 退出
机电学院电气工程系 上一页 下一页 回目录 退出 2.2 卡诺图化简法 2.3 VHDL硬件描述语言基础 2.1 逻辑代数
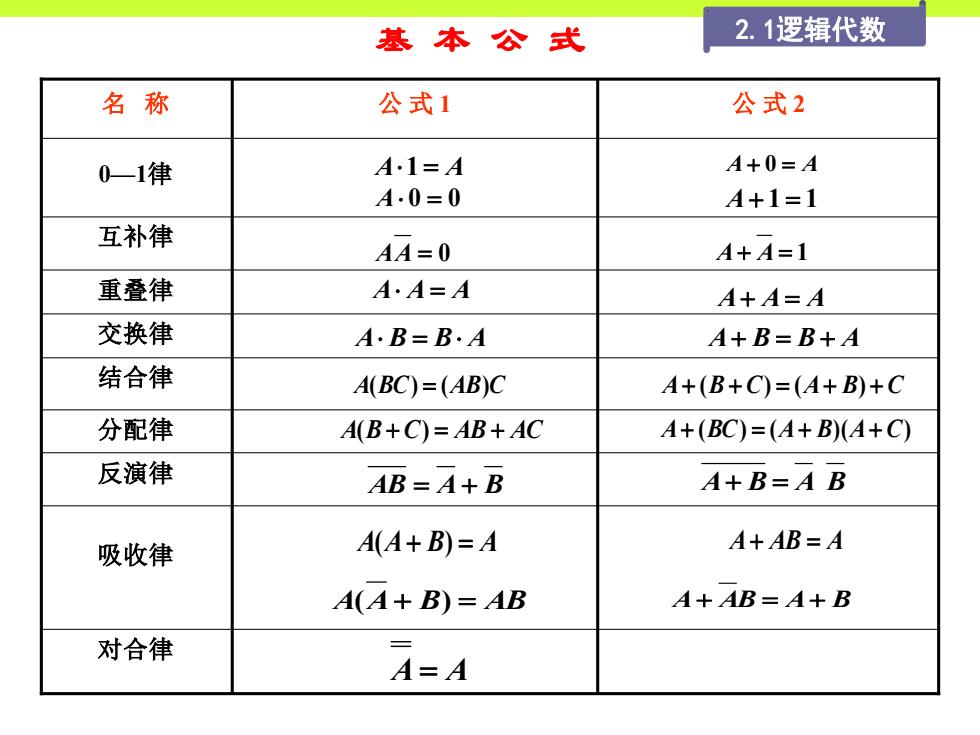
基本公式 2.1逻辑代数 名称 公式1 公式2 0-1律 A.1=A A+0=A A.0=0 A+1=1 互补律 AA=0 A+A=1 重叠律 A·A=A A十A=A 交换律 A·B=B.A 4+B=B+4 结合律 A(BC)=(AB)C A+(B+C)=(A+B)+C 分配律 A(B+C)=AB+AC A+(BC)=(A+B)(A+C) 反演律 AB=A+B A+B=A B 吸收律 A(A+B)=A A+AB=A A(A+B)=AB A+AB=A+B 对合律 A=A
机电学院电气工程系 上一页 下一页 回目录 退出 2.1 逻辑代数 一、逻辑代数的基本公式 吸收律 反演律 分配律 结合律 交换律 重叠律 互补律 公 式 1 0—1律 对合律 名 称 公 式 2 基 本 公 式 A1 = A A 0 = 0 A+ 0 = A A+ 1 = 1 AA = 0 A+ A = 1 A A = A A+ A = A A B = B A A+ B = B + A A(BC) = (AB)C A+ (B + C) = (A+ B) + C A(B + C) = AB + AC A+ (BC) = (A+ B)(A+ C) AB = A+ B A+ B = A B A(A+ B) = A A+ AB = A A(A+ B) = AB A+ AB = A+ B A = A 2.1逻辑代数
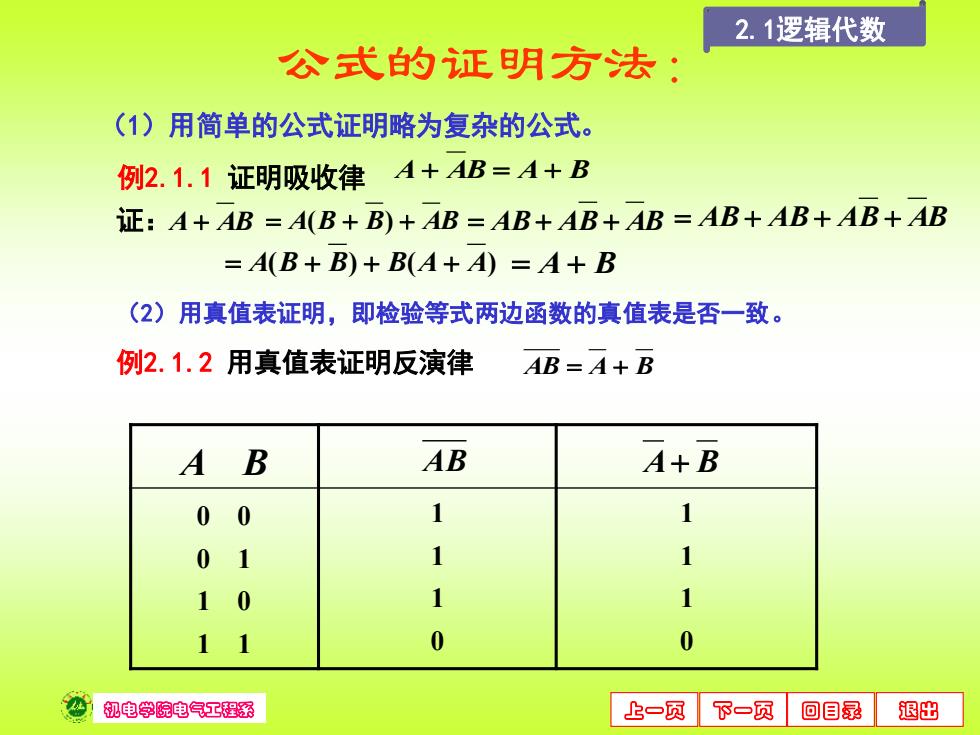
2.1逻辑代数 公式的证明方法: (1)用简单的公式证明略为复杂的公式。 例2.1.1证明吸收律A+AB=A+B 证:A+AB=A(B+B)+AB=AB+AB+AB=AB+AB+AB+AB =A(B+B)+B(A+A)=A+B (2)用真值表证明,即检验等式两边函数的真值表是否一致。 例2.1.2用真值表证明反演律AB=A+B A B AB A+B 00 1 1 01 1 1 10 1 1 11 0 0 机电容院电气工程器 上一页 下一页回目录退出
机电学院电气工程系 上一页 下一页 回目录 退出 公式的证明方法: (1)用简单的公式证明略为复杂的公式。 例2.1.1 证明吸收律 A + AB = A + B 证: A + AB = A(B + B) + AB = AB+ AB + AB = AB + AB + AB + AB = A(B + B) + B(A + A) = A + B A B 0 0 0 1 1 0 1 1 AB A+ B 例2.1.2 用真值表证明反演律 AB = A + B 1 1 1 0 1 1 1 0 (2)用真值表证明,即检验等式两边函数的真值表是否一致。 2.1逻辑代数

2.1逻辑代数 名称 公式1 公式2 A.1=A A+0=A 0一1律 A.0=0 A+1=1 互补律 44=0 A+A=1 重叠律 A·A=A A+A-A 交换律 A·B=B.A A+B=B+A 结合律 A(BC)=(AB)C A+(B+C)=(A+B)+C 分配律 A(B+C)=AB+AC A+(BC)=(A+B)(A+C) 反演律 AB=A十B A十B=AB A(A+B)=A A十AB=A 吸收律 A(A+B)=AB A+4B=A+B 对合律 A-A 对偶规则的基本内容是:如果两个逻辑函数表达式相等,那么它们 的对偶式也一定相等。 基本公式中的公式1和公式2就互为对偶式。 心祝电学院电气工繇 上-页下-页 回目录 退出
机电学院电气工程系 上一页 下一页 回目录 退出 二、逻辑代数的基本规则 ABC = A + BC = A + B + C 1 .代入规则 对于任何一个逻辑等式,以某个逻辑变量或逻辑函数同时取代 等式两端任何一个逻辑变量后,等式依然成立。 例如,在反演律中用BC去代替等式中的B,则新的等式仍成立: 2 .对偶规则 将一个逻辑函数L进行下列变换: ·→+,+ →· 0 → 1,1 → 0 所得新函数表达式叫做L的对偶式,用 表示。 ' L 对偶规则的基本内容是:如果两个逻辑函数表达式相等,那么它们 的对偶式也一定相等。 基本公式中的公式l和公式2就互为对偶 式。 吸收律 反演律 分配律 结合律 交换律 重叠律 互补律 公式1 0—1律 对合律 名称 公式2 A1 = A A 0 = 0 A+ 0 = A A+ 1 = 1 A A = A A+ A = A A B = B A A+ B = B + A A(BC) = (AB)C A+ (B + C) = (A+ B) + C A(B + C) = AB + AC A+ (BC) = (A+ B)(A+ C) AA = 0 A+ A = 1 AB = A+ B A+ B = A B A(A+ B) = AB A+ AB = A+ B A = A A(A+ B) = A A+ AB = A 2.1逻辑代数