
2.2卡诺图化简法 例2:将函数F=AB+AB+AB+C转换成最小项表达式。 解:F=AB+AB+AB+C=AB+AB·AB.C =AB+(A+B(A+B)C =AB+ABC+ABC =AB(C+C)+ABC+ABC ABC+ABC+ABC+ABC =m+m6+m3+ms=∑m(3,5,6,7) 机电学碗电气工程系 上一页 下一页回目录 退出
机电学院电气工程系 上一页 下一页 回目录 退出 解: F = AB + AB + AB + C = AB + AB AB C = AB(C + C) + ABC + ABC =m7+m6+m3+m5=∑m(3,5,6,7) 例2: 将函数 F = AB + AB + AB + C 转换成最小项表达式。 = AB + (A+ B)(A+ B)C = AB+ ABC + ABC = ABC+ ABC + ABC + ABC 2.2 卡诺图化简法

2.2卡诺图化简法 二、卡诺图及其逻辑函数的卡诺图表示法 1.相邻最小项 如果两个最小项中只有一个变量互为反变量,其余变量均相同,则 称这两个最小项为逻辑相邻,简称相邻项。 如最小项ABC和ABC就是相邻最小项。 如果两个相邻最小项出现在同一个逻辑函数中,可以合并为一项,同 时消去互为反变量的那个量。 如:ABC+ABC=AC(B+B)=AC 2.卡诺图 一个小方格代表一个最小项,然后将这些最小项按照相 邻性排列起来。即用小方格几何位置上的相邻性来表示最 小项逻辑上的相邻性。 心祝电袋院电气工繇 上一页 下一页 回目录 退出
机电学院电气工程系 上一页 下一页 回目录 退出 二、卡诺图及其逻辑函数的卡诺图表示法 1.相邻最小项 如果两个最小项中只有一个变量互为反变量,其余变量均相同,则 称这两个最小项为逻辑相邻,简称相邻项。 如果两个相邻最小项出现在同一个逻辑函数中,可以合并为一项,同 时消去互为反变量的那个量。 如最小项ABC 和 ABC 就是相邻最小项。 如: ABC + ABC = AC(B + B) = AC 2 .卡诺图 一个小方格代表一个最小项,然后将这些最小项按照相 邻性排列起来。即用小方格几何位置上的相邻性来表示最 小项逻辑上的相邻性。 2.2 卡诺图化简法
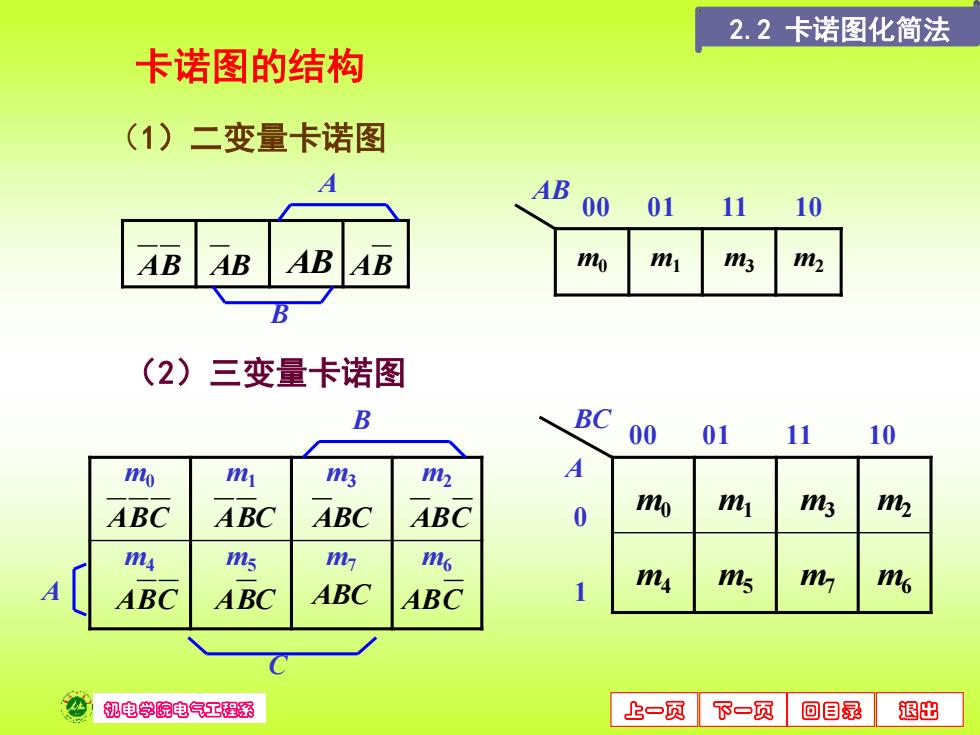
2.2卡诺图化简法 卡诺图的结构 (1)二变量卡诺图 AB 00 01 11 10 AB AB AB AB mo my m3 m B (2)三变量卡诺图 B BC 00 01 11 10 mo m 3 2 A ABC ABC ABC ABC 0 mo m l 2 ma ms m 6 mi ABC ABC ms n ms ABC ABC 心机电学院电气工程系 上一页 下一页 回目录 退出
机电学院电气工程系 上一页 下一页 回目录 退出 卡诺图的结构 (1)二变量卡诺图 AB AB AB AB A B m0 m1 m3 m2 AB 00 01 11 10 m0 m1 m3 m2 m4 m5 m7 m6 ABC ABC ABC ABC A ABC ABC ABC ABC B C m0 m1 m3 m2 m4 m5 m7 m6 BC 00 01 11 10 A 0 1 (2)三变量卡诺图 2.2 卡诺图化简法
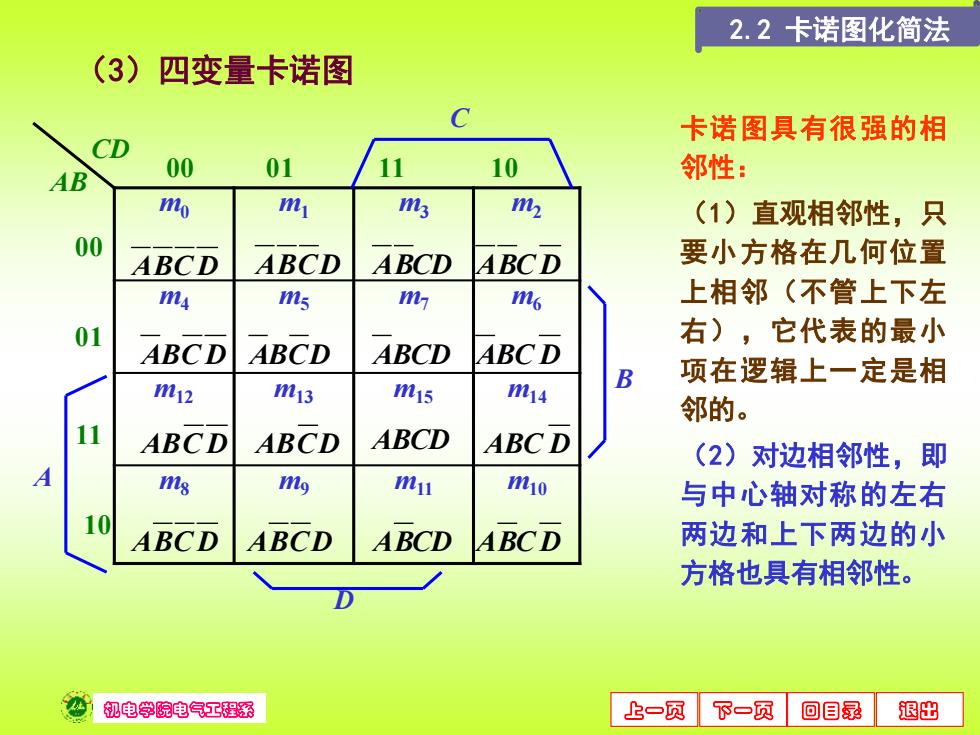
2.2卡诺图化简法 (3)四变量卡诺图 卡诺图具有很强的相 CD 00 01 11 10 邻性: mo m 3 h (1)直观相邻性,只 00 ABCD ABCD ABCD ABCD 要小方格在几何位置 4 ms ms 上相邻(不管上下左 01 右),它代表的最小 ABCD ABCD ABCD ABC D 项在逻辑上一定是相 m12 m13 m15 m14 邻的。 11 ABCD ABCD ABCD ABC D (2)对边相邻性,即 y ms my mu mio 与中心轴对称的左右 10 ABCD ABCD ABCD ABC D 两边和上下两边的小 方格也具有相邻性。 机电学院电气工程系 上一页 下一页 回目录 退出
机电学院电气工程系 上一页 下一页 回目录 退出 m0 m1 m3 m2 m4 m5 m7 m6 m12 m13 m15 m14 m8 m9 m11 m10 ABC D ABCD ABCD ABC D ABC D ABCD ABCD ABC D ABC D ABCD ABCD ABC D ABC D ABCD ABCD ABC D C D A B CD 00 01 11 10 AB 00 01 11 10 卡诺图具有很强的相 邻性: (1)直观相邻性,只 要小方格在几何位置 上相邻(不管上下左 右),它代表的最小 项在逻辑上一定是相 邻的。 (2)对边相邻性,即 与中心轴对称的左右 两边和上下两边的小 方格也具有相邻性。 (3)四变量卡诺图 2.2 卡诺图化简法