
日录 QCD的手征对称性线性。模型 PGB所量 丰线性g模型低晚手有效设托t:Wess-Zumino-Vitten 000●000000 0000000000000 000000000 0000 00000000000000000000000000 矢量流守恒与轴矢流部分守恒 B-deory -decoy 3衰变:C8=- 若,(1-s)e.51-9u. 4衰变:Cu=一 (I-p)..(1-) V2 考虑到B章交可能的滋作用修E:c雪=一9告,)-a(n.a1-地 gv(0)=1 84(0)=1.22士0.02 为什么矢量流顶角不受强作用影响?而轴矢流顶角受部分强作用影响? 类似的问题:为什么实验测的质子电荷和正电子电荷完全一样?强作用修正螺去了? 强作用从初态绝热地引入,到终态再绝热地撒除→只要电荷守恒,质子电荷就不受强作用修正! 电流守恒:0产=0→ =0g = x°(x)→质子电荷就不受强作用修正 弱作用的矢量流守恒(CVC)假设保证矢量流顶角不受强作用修正gv(O)=1 王青( 柳惠手征对称性及其破缺
✽➵ QCD✛➹✍é→✺ ❶✺σ✜✳ PGB➓þ ➎❶✺σ✜✳ ✩❯➹✍❦✟✳➻þ Wess-Zumino-Witten➅ ➙þ✻➴ð❺➯➙✻Ü➞➴ð βP❈➭ Lβ = − GF √ 2 ψpγ µ (1−γ5)ψnψeγµ(1−γ5)ψνe µP❈➭ Lµ = − GF √ 2 ψµγ µ (1−γ5)ψνµ ψeγµ(1−γ5)ψνe ⑧➘✔βP❈➀❯✛r❾❫❄✔➭ L eff β = − GF √ 2 ψpγ µ [gV (q 2 ) − gA(q 2 )γ5]ψnψeγµ(1 − γ5)ψν gV (0) = 1 gA(0) = 1.22 ± 0.02 ➃➓♦➙þ✻➸✍Ø➱r❾❫❑➃? ✌➯➙✻➸✍➱Ü➞r❾❫❑➃? ❛q✛➥❑: ➃➓♦➣✟ÿ✛➓❢❃ÖÚ✔❃❢❃Ö✑✜➌✘?r❾❫❄✔❂✖✡? r❾❫❧Ð✕ý✾✴Ú❭,✔➟✕✷ý✾✴➆Ø⇒➄❻❃Ö➴ð,➓❢❃ÖÒØ➱r❾❫❄✔! ❃✻➴ð: ∂µj µ = 0 ⇒ dQ dt = 0 Q = Z d 3 x j0 (x) ⇒ ➓❢❃ÖÒØ➱r❾❫❄✔ ❢❾❫✛➙þ✻➴ð(CVC) ❜✗ ✂②➙þ✻➸✍Ø➱r❾❫❄✔ gV (0) = 1 ✜➇ (➌✉➀➷) â❢♥Ø❀❑ ➹ ✍ é → ✺ ✾ Ù ➺ ✧
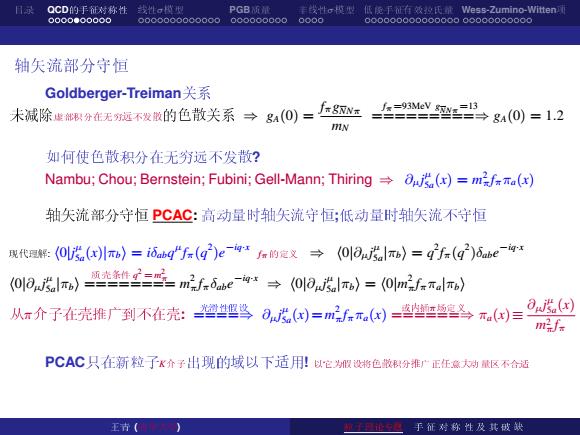
QCD的手征对称性 线性o横型 PGB 丰线性g模型低晚手有效设托t:Wess-Zumino-Vitten 0000●00000 0000000000000 000000000 0000 00000000000000000000000000 轴矢流部分守恒 Goldberger--Treiman关系 未减除能限分无不发散的色散关系→g0)=在江g40)=12 W 如何使色散积分在无穷远不发散? Nambu;Chou;Bernstein;Fubini;Gell-Mann;Thiring =(x)=mf(x) 轴矢流部分守恒PCAC:高动量时轴矢流守恒;低动量时轴矢流不守恒 现代解:(0l5(x)川b)=i6 Sabq"fx(q)e-9xa的定义→《(Ol3 ajso mb)=qfn(g2)iabe-ig (Ol6lr)g=至m2f.dwe→(O6l)=Om2fmal} 从m介子在壳推广到不在壳:鸟0()=m2间=望笔元付=可但 miafs PCAC只在新粒子x介子出现的域以下适用以它为假设将色散积分推广正任意大动量区不合适 王青( 柳论息手征对称性及其破缺
✽➵ QCD✛➹✍é→✺ ❶✺σ✜✳ PGB➓þ ➎❶✺σ✜✳ ✩❯➹✍❦✟✳➻þ Wess-Zumino-Witten➅ ➯➙✻Ü➞➴ð Goldberger-Treiman✬❳ ➍⑦Ø❏Ü➮➞✸➹→✎Ø✉Ñ✛ÚÑ✬❳ ⇒ gA(0) = fπgNNπ mN fπ=93MeV gNNπ=13 =========⇒ gA(0) = 1.2 ❳Û➛ÚÑ➮➞✸➹→✎Ø✉Ñ? Nambu; Chou; Bernstein; Fubini; Gell-Mann; Thiring ⇒ ∂µj µ 5a (x) = m 2 πfππa(x) ➯➙✻Ü➞➴ð PCAC: ♣➘þ➒➯➙✻➴ð;✩➘þ➒➯➙✻Ø➴ð ②➇♥✮: h0|j µ 5a (x)|πbi = iδabq µ fπ(q 2 )e −iq·x fπ✛➼➶ ⇒ h0|∂µj µ 5a |πbi = q 2 fπ(q 2 )δabe −iq·x h0|∂µj µ 5a |πbi ➓❾❫❻ q 2 =m 2 π ======== m 2 πfπδabe −iq·x ⇒ h0|∂µj µ 5a |πbi = h0|m 2 πfππa|πbi ❧π✵❢✸❾í✷✔Ø✸❾: ✶✇✺❜✗ ====⇒ ∂µj µ 5a (x)=m 2 πfππa(x) ➼❙✂π⑤➼➶ ======⇒ πa(x)≡ ∂µj µ 5a (x) m2 πfπ PCAC➄✸★â❢K✵❢Ñ②✛➁➧❡➲❫! ➧➜➃❜✗òÚÑ➮➞í✷✔❄➾➀➘þ➠ØÜ➲ ✜➇ (➌✉➀➷) â❢♥Ø❀❑ ➹ ✍ é → ✺ ✾ Ù ➺ ✧
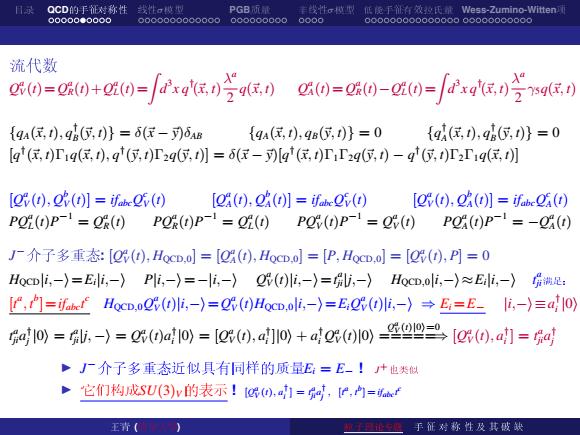
日录 QCD的手征对称性线性。模型 PGB所量 丰线性c模低晚手有效女托Wess-Zumino-Vitten 00000●0000 0000000000000 000000000 流代数 )=CH)+)=x(-()=x {qA(民,),qA(,)}=6(民-月5AB {qa(民,),qs(,)}=0 {qA(民,),9g,)}=0 [q(民,)Tq(民,),q(位,)P2q位,】=6(-[g(民,)T「2q位,)-q(位,t)rzT1q(民,] [g(),Q(0]=faQ() [g(),Q()]=ifQ5() [g(0),Q(】=feQ(0) POi(1)P-=(t)POR(t)P-=i(t) Pg()P-1=Q(0)Pg(I)P-I=-Q() J厂介子多重态:[g(),HocD.d=[g(),HocD.0=[P,HocD.0=[g(),P月=0 HocDi,-〉=Ei,-〉Pi,-〉=-i,-〉Q()i,-〉=,-〉HocD,oli,-)≈Ei,-〉层满是: [,]=ia上HocD,oQ()l,-)=Q(0)HocD.oli,-〉=EO(0)li,-〉→E=Ei,-)三aI0) ol0=,-)=Q(0)alo=e0,alIo)+ae(o)l0)三[ed),a1=网 ·J厂介子多重态近似具有同样的质量E=E-!+也类似 >它们构成SU(3)v的表示!四o,1=g,,门=f 子手征对称性及其破缺
✽➵ QCD✛➹✍é→✺ ❶✺σ✜✳ PGB➓þ ➎❶✺σ✜✳ ✩❯➹✍❦✟✳➻þ Wess-Zumino-Witten➅ ✻➇ê Q a V (t)=Q a R(t)+Q a L(t)=Z d 3 x q † (~x, t) λ a 2 q(~x, t) Q a A(t)=Q a R(t)−Q a L(t)=Z d 3 x q † (~x, t) λ a 2 γ5q(~x, t) {qA(~x, t), q † B (~y, t)} = δ(~x −~y)δAB {qA(~x, t), qB(~y, t)} = 0 {q † A (~x, t), q † B (~y, t)} = 0 [q † (~x, t)Γ1q(~x, t), q † (~y, t)Γ2q(~y, t)] = δ(~x −~y)[q † (~x, t)Γ1Γ2q(~y, t) − q † (~y, t)Γ2Γ1q(~x, t)] [Q a V (t), Q b V (t)] = ifabcQ c V (t) [Q a A(t), Q b A(t)] = ifabcQ c V (t) [Q a V (t), Q b A(t)] = ifabcQ c A(t) PQa L(t)P −1 = Q a R(t) PQa R(t)P −1 = Q a L(t) PQa V (t)P −1 = Q a V (t) PQa A(t)P −1 = −Q a A(t) J −✵❢õ➢✕: [Q a V (t), HQCD,0] = [Q a A(t), HQCD,0] = [P, HQCD,0] = [Q a V (t), P] = 0 HQCD|i,−i=Ei|i,−i P|i,−i=−|i,−i Q a V (t)|i,−i=t a ji|j,−i HQCD,0|i,−i≈Ei|i,−i t a ji÷✈➭ [t a , t b ]=ifabct c HQCD,0Q a V (t)|i,−i=Q a V (t)HQCD,0|i,−i=EiQ a V (t)|i,−i ⇒ Ei =E− |i,−i≡a † i |0i t a jia † j |0i = t a ji|j, −i = Q a V (t)a † i |0i = [Q a V (t), a † i ]|0i + a † i Q a V (t)|0i Q a V (t)|0i=0 =====⇒ [Q a V (t), a † i ] = t a jia † j I J −✵❢õ➢✕❈qä❦Ó✘✛➓þEi = E− ! J+➃❛q I ➜❶✟↕SU(3)V✛▲➠ ! [Q a V (t), a † i ] = t a jia † j , [t a , t b ]=ifabct c ✜➇ (➌✉➀➷) â❢♥Ø❀❑ ➹ ✍ é → ✺ ✾ Ù ➺ ✧

QCD的手征对称性线性模型 PGBM量 Wess-Zumino-Witten 000000●000 000000000 Q(0=Q(0+Q(0)= x运)3民,) ()=()-Ci()=dxq.() [g(0),Q(0]=ifkQ5() [Q(0),Qg(0)]=iQ() [g(o),Q(c]=if(0) PQ(0)P-1=QR() POR(1)P=i(t) PQ()P-=Q() PO()P=-(t) J厂介子多重态:Q()i,-〉=,-〉li,-〉三aI0)[(0,a】=a Q()i,-〉≡s,+〉Pls,+)=s,+〉HocD.oQ然(0i,-〉=Q(0)Hocp.oli,-〉=E_-Q()i,-〉 HocD,0,+〉=E+,+〉→ E+=E-字称简并 解顶存在单粒子股斑 Q(0)li,-〉=QaI0)= [()ao) a()o) a对称变换导致的单粒子态项 多粒子态项 Q(l0)≠0即可解顶Q()O)=0一SU(3)2×SU(3)R一SU(3)v理论证踢?Q()10)=b410〉 HocD.ob0)=HocD.0(r)10)=(t)HocD.o10)=0 PBIO)=POA(r)10)=POR(r)P-PI0)=-()10) I0)≡1(0)》 (r)(0))=[(r).B=(r)(r)o)=[(r),()0)=ifahe(r)o)=ifahBo) [g(),bJ=ilQ呢(t)lo(o)》=ifabe(O)》 →()l(p)》=ifabe(p)》 手征对称性极其破站
✽➵ QCD✛➹✍é→✺ ❶✺σ✜✳ PGB➓þ ➎❶✺σ✜✳ ✩❯➹✍❦✟✳➻þ Wess-Zumino-Witten➅ Q a V (t)=Q a R(t)+Q a L(t)=Z d 3 x q † (~x, t) λ a 2 q(~x, t) Q a A(t)=Q a R(t)−Q a L(t)=Z d 3 x q † (~x, t) λ a 2 γ5q(~x, t) [Q a V (t), Q b V (t)] = ifabcQ c V (t) [Q a A(t), Q b A(t)] = ifabcQ c V (t) [Q a V (t), Q b A(t)] = ifabcQ c A(t) PQa L(t)P −1 = Q a R(t) PQa R(t)P −1 = Q a L(t) PQa V (t)P −1 = Q a V (t) PQa A(t)P −1 = −Q a A(t) J −✵❢õ➢✕: Q a V (t)|i, −i = t a ji|j, −i |i, −i ≡ a † i |0i [Q a V (t), a † i ] = t a jia † j Q a A(t)|i,−i≡˜t a si|s,+i P|s,+i=|s,+i HQCD,0Q a A(t)|i,−i=Q a A(t)HQCD,0|i,−i=E−Q a A(t)|i,−i HQCD,0˜t a si|s, +i = E+˜t a si|s, +i ⇒ E+ = E− ❽→④➾ ✮➸: ⑧✸üâ❢❜✗! Q a A(t)|i, −i = Q a Aa † i |0i = [Q a A(t), a † i ]|0i | {z } a † i é→❈❺✓➋✛üâ❢✕➅ + a † i Q a A(t)|0i | {z } õâ❢✕➅ Q a A(t)|0i 6= 0 ❂➀✮➸ Q a V (t)|0i = 0 → SU(3) L × SU(3) R → SU(3) V ♥Ø②➨➸ Q a A(t)|0i = ˜b † a |0i HQCD,0 ˜b † a |0i = HQCD,0Q a A(t)|0i = Q a A(t)HQCD,0|0i = 0 P˜b † a |0i = PQa A(t)|0i = PQa A(t)P −1 P|0i = −Q a A(t)|0i ˜b † a |0i ≡ |φ a (0)i Q a V (t)|φ b (0)i = [Q a V (t), ˜b † b ]|0i = Q a V (t)Q b A(t)|0i = [Q a V (t), Q b A(t)]|0i = ifabcQ c A(t)|0i = ifabc˜b † c |0i [Q a V (t), ˜b † b ] = ifabc˜b † c Q a V (t)|φ b (0)i = ifabc|φ c (0)i ⇒ Q a V (t)|φ b (p)i = ifabc|φ c (p)i ✜➇ (➌✉➀➷) â❢♥Ø❀❑ ➹ ✍ é → ✺ ✾ Ù ➺ ✧

日录 QCD的手征对称性线性。横型 PGB所量 丰线g型低手有效Wess-Zumino-Wen 0000000●00 0000000000000 000000000 赝标介子八重态:T=Q Y=子0 Q(lp(p)》=fsc中(p)》 K(-2) K*(吃) (T3,Y): π(-1,0) π(0,0) (0,0) π+(1,0) K(-2- abc 123147 156 246257 345367 458678 fabe - - T3(p1)-i2)=-(Ip〉-i2)】 Y(p〉-i2)=0 T3(p1〉+2)=lp〉+2) Y(p1)+p2)=0 7(〉-s)=-5)-s》y(lo〉-os》=-((Io〉-os》 T(I)+s)=)+s)》 Y(Ip4〉+is)=lp4〉+ps〉 T3(106)-il6))=(16)-ilo)) Y(p6)-)=-(I%)-ip) n(1s)+o》=-s)+l物》 Y(o〉+i)=ls+n T3)=Ylp〉=T乃s)=Yls)=0 模青( 手征对称性及其破缺
✽➵ QCD✛➹✍é→✺ ❶✺σ✜✳ PGB➓þ ➎❶✺σ✜✳ ✩❯➹✍❦✟✳➻þ Wess-Zumino-Witten➅ ✣■✵❢❧➢✕: T3 = Q 3 V Y = √2 3 Q 8 V Q a V (t)|φ b (p)i = ifabc|φ c (p)i K 0 (− 1 2 , 1) K + ( 1 2 , 1) φ a (T3, Y) : π −(−1, 0) π 0 (0, 0) η(0, 0) π + (1, 0) K −(− 1 2 , −1) K¯ 0 ( 1 2 , −1) abc 123 147 156 246 257 345 367 458 678 fabc 1 1 2 − 1 2 1 2 1 2 1 2 − 1 2 √ 3 2 √ 3 2 T3(|φ1i − i|φ2i) = −(|φ1i − i|φ2i) Y(|φ1i − i|φ2i) = 0 T3(|φ1i + i|φ2i) = |φ1i + i|φ2i Y(|φ1i + i|φ2i) = 0 T3(|φ4i − i|φ5i) = − 1 2 (|φ4i − i|φ5i) Y(|φ4i − i|φ5i) = −(|φ4i − i|φ5i) T3(|φ4i + i|φ5i) = 1 2 (|φ4i + i|φ5i) Y(|φ4i + i|φ5i) = |φ4i + i|φ5i T3(|φ6i − i|φ7i) = 1 2 (|φ6i − i|φ7i) Y(|φ6i − i|φ7i) = −(|φ6i − i|φ7i) T3(|φ6i + i|φ7i) = − 1 2 (|φ6i + i|φ7i) Y(|φ6i + i|φ7i) = |φ6i + i|φ7i T3|φ3i = Y|φ3i = T3|φ8i = Y|φ8i = 0 ✜➇ (➌✉➀➷) â❢♥Ø❀❑ ➹ ✍ é → ✺ ✾ Ù ➺ ✧