上海交通大学：《概率论与数理统计》课程教学资源（课件讲稿）11、随机变量的数字特征 §4.3 常用随机变量的期望与方差 §4.4 协方差和相关系数 §4.5 矩和协方差矩阵

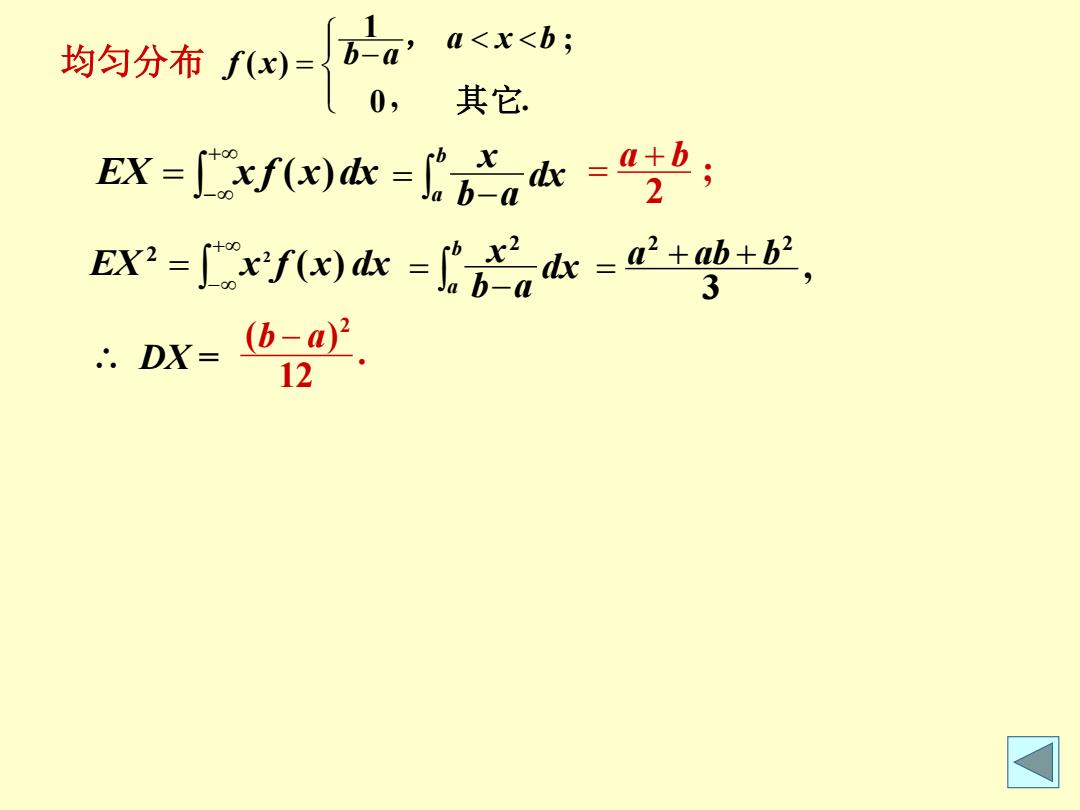
均的分布四 axxchi 其它 BX=fw=6ac-生 xX2=∫e/)==a++E, 3 :DX=(b-a. 12 ☑

        0 , . ; 1 ( ) 其 它 ， a x b b a f x dx b a b x a   ; 2 a  b  dx b a b x a   2 , 3 2 2 a  ab  b  . 12 ( ) 2 b  a EX x f x dx     ( ) EX x f x dx     ( ) 2 2 均匀分布 ∴ DX =

指数分布= EX=0xes是tet=2=元 "x"e *dx =I(r)(r>0) T(r+1)=r(r) r(1)=n: r为整数n时，T(n+1)=n! EX)=2e兰京eh是-是， Dx=是-党=亮. ✉

       0. 0 , , 0; ( ) x e x f x x  EX x e dx x     0   t e dt x t t      0 1     (2)  ； 1  E X x e dx x     0 2 2 ( )   t e dt x t t      0 2 2 1   2 (3)    , 2 2   2 2 ) 1 ( 2   DX   指数分布 . 1 2   ( ) ( 0) 0 1        x e dx r r r x   (r 1)  r(r) r 为整数 n 时， (n+1) = n! (1)= n!

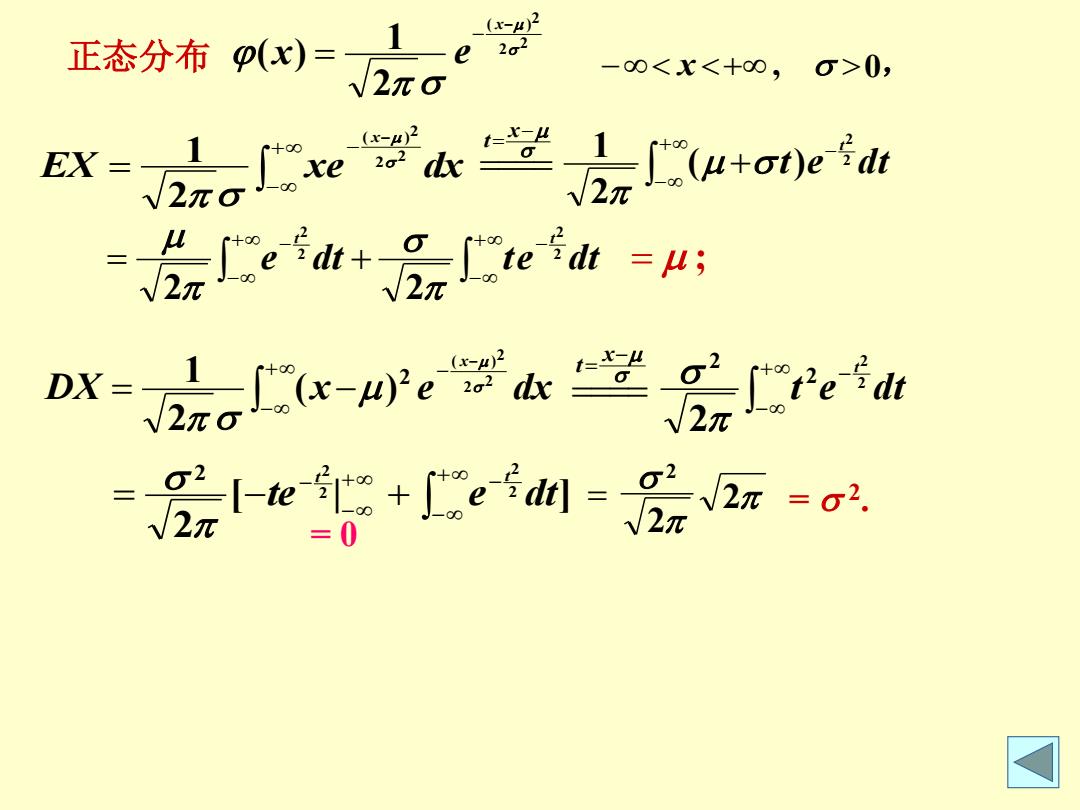
正态分布p(x)= 2o2 -0<X<+0,g>0 (x-) e+e=A oN2aa,学.m 2元e+e训-azr-o2 0 ☑

2 2 2 ( ) 2 1 ( )         x x e EX xe dx x       2 2 2 ( ) 2 1     t e dt t x t         2 2 ( ) 2 1      e dt te dt t t           2 2 2 2 2 2      ; 正态分布  x  ,  0， DX x e dx x        2 2 2 ( ) 2 ( ) 2 1      t e dt t x t        2 2 2 2 2    [ | ] 2 2 2 2 2 2 te e dt t t                2 2 2  = 2 . = 0

另外，几何分布X~G(p) EX=DX=D1 超几何分布X~H(n,M,N) E=4, N' DX=IM(N-M)(N-n) N2(N-1) 更多的可查P132附表1. 例1(P.165例20)设(X,Y)~N(a,b,o1,o,p),求E(2X-3Y+1). 解由条件知X~N(a,o),Y~N(b,o),.EX=M,EY=b, ∴.E(2X-3Y+1)=E(2X)-E(3)+E(1)=2a-3b+1

几何分布 X ~ G( p) ; p2 q , DX  1 p EX  超几何分布 X ~ H(n, M, N) . ( 1) ( ) ( ) 2     N N nM N M N n ， DX N EX  nM 另外， 更多的可查 P132 附表1. 例1(P.165 例20)设 ( , ) ~ ( , , , , ), 2 2 2 X Y N a b 1   求 E(2X-3Y+1). 解 由条件知 ~ ( , ), ~ ( , ), 2 2 2 X N a 1 Y N b  ∴ EX = a , EY = b, ∴ E(2X-3Y+1)= E(2X)-E(3Y)+ E( 1) = 2a - 3b + 1