
注 1.数乘矩阵是数)去乘A中的每一个元素 2.若k4=0,则或有k=0或有A=0. 3.加法与数乘运算合称为矩阵的线性运算 炬阵线性运算的两个应用 ©多次线件运算式的化简,例: 3(2X+0+4(3X+20=.=18X+11Y ●两个原内部约定现可合法化:某行乘:两行相加 张鞘同济大学 5/42
. ⌞:. . 1. 数乘矩阵是数 λ 去乘A中的每一个元素. 2. 若 kA = 0, 则或有 k = 0 或有 A = 0. 3. 加法与数乘运算合称为矩阵的线性运算. . 矩阵线性运算的њѠ应用 . . .1 多次线性运算式的化简, 例: 3(2X + Y) + 4(3X + 2Y) = · · · = 18X + 11Y. .2 两个原内部约定现可合法化:“某行乘 k”;“两行相加”. ᕖ㦿 (ੂ⎄ཝᆜ) 线性ԙ数 5 / 42

注: 1.数乘矩阵是数)去乘A中的每一个元素 2.若k4=0,则或有k=0或有A=0. 3.加法与数乘运算合称为矩阵的线性运算 矩阵线性运算的两个应用 多次线运式的化简例: 3(2T半月+43X+2月==18T牛117 ©两个原内部约定现可合法化:某行乘:两行相州 张鞘同济大学 5/42
. ⌞:. . 1. 数乘矩阵是数 λ 去乘A中的每一个元素. 2. 若 kA = 0, 则或有 k = 0 或有 A = 0. 3. 加法与数乘运算合称为矩阵的线性运算. . 矩阵线性运算的њѠ应用 . . .1 多次线性运算式的化简, 例: 3(2X + Y) + 4(3X + 2Y) = · · · = 18X + 11Y. .2 两个原内部约定现可合法化:“某行乘 k”;“两行相加”. ᕖ㦿 (ੂ⎄ཝᆜ) 线性ԙ数 5 / 42
注: 1.数乘矩阵是数入去乘A中的每一个元素 2.若k4=0,则或有k=0或有A=0. 3.加法与数乘运算合称为矩阵的线性运算 矩阵线性运算的两个应用 ①多次线性运算式的化简,例: 3(2X+)+4(3X+2)=·.·=18X+11Y. ©两个原内部约定现可合法化:某行乘:两行相州 张鞘同济大学 5/42
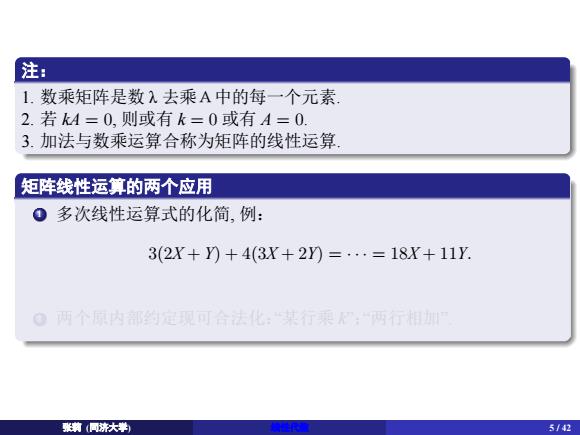
. ⌞:. . 1. 数乘矩阵是数 λ 去乘A中的每一个元素. 2. 若 kA = 0, 则或有 k = 0 或有 A = 0. 3. 加法与数乘运算合称为矩阵的线性运算. . 矩阵线性运算的њѠ应用 . . .1 多次线性运算式的化简, 例: 3(2X + Y) + 4(3X + 2Y) = · · · = 18X + 11Y. .2 两个原内部约定现可合法化:“某行乘 k”;“两行相加”. ᕖ㦿 (ੂ⎄ཝᆜ) 线性ԙ数 5 / 42

注: 1.数乘矩阵是数入去乘A中的每一个元素 2.若k4=0,则或有k=0或有A=0. 3.加法与数乘运算合称为矩阵的线性运算 矩阵线性运算的两个应用 ①多次线性运算式的化简,例: 3(2X+)+4(3X+2)=·.·=18X+11Y. @两个原内部约定现可合法化:“某行乘”:“两行相加” 张鞘同济大学 5142
. ⌞:. . 1. 数乘矩阵是数 λ 去乘A中的每一个元素. 2. 若 kA = 0, 则或有 k = 0 或有 A = 0. 3. 加法与数乘运算合称为矩阵的线性运算. . 矩阵线性运算的њѠ应用 . . .1 多次线性运算式的化简, 例: 3(2X + Y) + 4(3X + 2Y) = · · · = 18X + 11Y. .2 两个原内部约定现可合法化:“某行乘 k”;“两行相加”. ᕖ㦿 (ੂ⎄ཝᆜ) 线性ԙ数 5 / 42

三、矩阵的乘法 L.定义4(p.34):设矩阵A=(a)mxs和B=(b)5xm满足: A的列数=B的行数, (可乘性条件) 则定义乘积(AB)为一个矩阵C=(c)mxm,其中 cy anby+..+aisby =i=1aikby, (i=1,…,m;j=1,…,n) 2.语言表述:4的第(行和B的第列的对应元素乘积之和 3.思考(关于可乘性条件 门)B可乘是否B对一定可乘? 卫两个房何可地 3同的可 张鞘同济大学 性物 6/42
三、矩阵的乘法 1. 定义 4(p.34):设矩阵 A = (aij)m×s 和 B = (bij)s×n 满足: A 的列数 = B 的行数, (可乘性条件) 则定义乘积(AB)为一个矩阵 C = (cij)m×n, 其中 cij = ai1b1j + · · · + aisbsj = ∑s k=1 aikbkj , (i = 1, · · · , m; j = 1, · · · , n) 2. 语言表述:A 的第 i 行和 B 的第 j 列的对应元素乘积之和. 3. 思考(关于可乘性条件) (1) AB 可乘是否 BA 一定可乘? (2) 两个方阵何时可乘? (3) A 和 A 何时可乘? ᕖ㦿 (ੂ⎄ཝᆜ) 线性ԙ数 6 / 42