
在实际应用中,希望输入空间中二个相近的输入能够 产生交叠的映射(泛化)。而对于二个相距较远的输入能产 生各自独立的响应。CMAC网的映射过程就能保证实现 这种要求。对于任何给定的输入,映射函数指向几(如 )个地址表A中的存储地址,这些地址是处在联想单元 中,称之为激活的联想单元,在某一具体的非线性函数 学习过程中,激活的联想单元数目M是CMAC设计的一 个固定参数。一般满足 M=0.01Ap (7.2) 式中4地址表中的总元素 11
11 在实际应用中,希望输入空间中二个相近的输入能够 产生交叠的映射(泛化)。而对于二个相距较远的输入能产 生各自独立的响应。CMAC网的映射过程就能保证实现 这种要求。对于任何给定的输入,映射函数f指向几(如 M)个地址表A中的存储地址,这些地址是处在联想单元 中,称之为激活的联想单元,在某一具体的非线性函数 学习过程中,激活的联想单元数目M是CMAC设计的一 个固定参数。一般满足 M A =0.01 p (7.2) 式中 Ap 地址表中的总元素
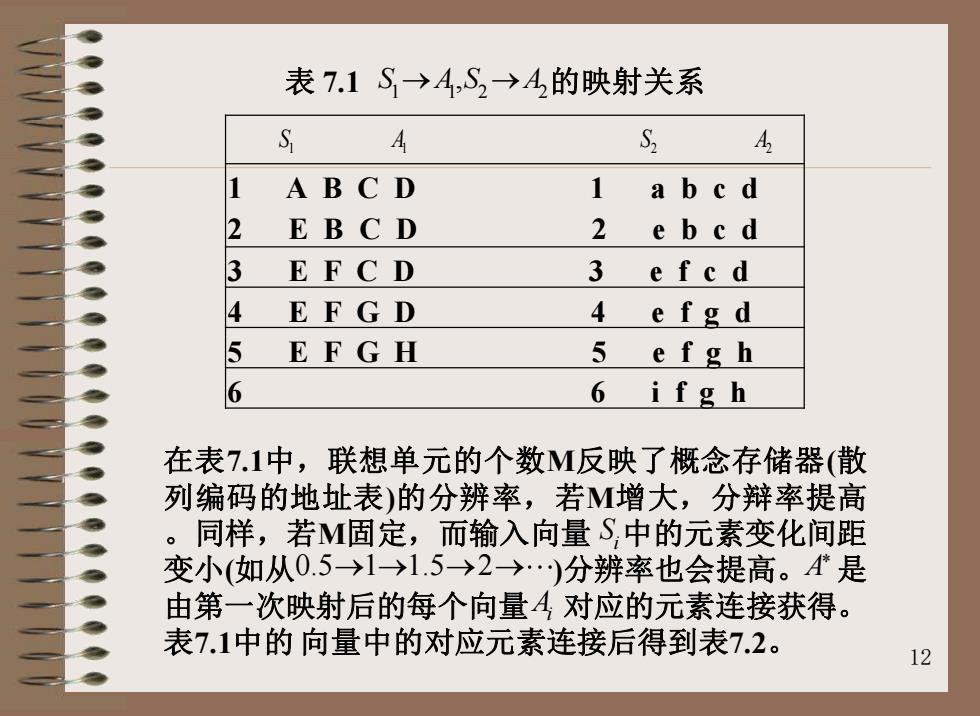
表7.1S→4,S2→A的映射关系 S S3 4 1 ABCD 1 a bc d 2 EB CD 2 ebcd 3 EFCD 3 e fc d 4 EFGD 4 e fg d 5 EFGH 5 e fgh 6 i f g h 6 在表7.1中,联想单元的个数M反映了概念存储器(散 列编码的地址表)的分辨率,若M增大,分辩率提高 。同样,若M固定,而输入向量S,中的元素变化间距 变小(如从0.5→1→1.5→2→)分辨率也会提高。是 由第一次映射后的每个向量A对应的元素连接获得。 表7.1中的向量中的对应元素连接后得到表7.2。 12
12 表 7.1 S A S A 1 1 2 2 → → , 的映射关系 1 A B C D 1 a b c d 2 E B C D 2 e b c d 3 E F C D 3 e f c d 4 E F G D 4 e f g d 5 E F G H 5 e f g h 6 6 i f g h 1 1 2 A2 S A S 在表7.1中,联想单元的个数M反映了概念存储器(散 列编码的地址表)的分辨率,若M增大,分辩率提高 。同样,若M固定,而输入向量 中的元素变化间距 变小(如从 )分辨率也会提高。 是 由第一次映射后的每个向量 对应的元素连接获得。 表7.1中的 向量中的对应元素连接后得到表7.2。 i S 0.5 1 1.5 2 → → → → A* i A
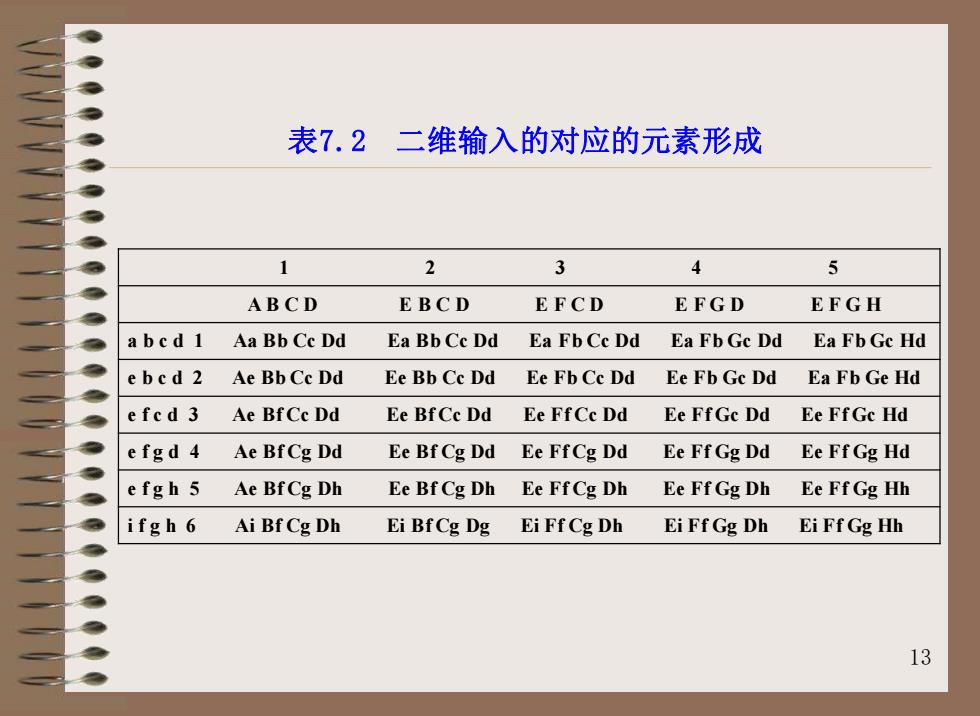
表7.2二维输入的对应的元素形成 1 2 3 4 5 ABCD EBCD EFCD EFGD EFGH Aa Bb Cc Dd Ea BbCe Dd Ea FbCe Dd Ea Fb Ge Dd Ea Fb Gc Hd Ae Bb Cc Dd Ee Bb Cc Dd Ee Fb Ce Dd Ee Fb Gc Dd Ea Fb Ge Hd fcd 3 Ae BfCc Dd Ee BfCc Dd Ee FfCc Dd Ee FfGc Dd Ee FfGc Hd efgd 4 Ae BfCg Dd Ee Bf Cg Dd Ee FfCg Dd Ee Ff Gg Dd Ee Ff Gg Hd e fgh 5 Ae BfCg Dh Ee Bf Cg Dh Ee FfCg Dh Ee Ff Gg Dh Ee Ff Gg Hh ifgh 6 Ai Bf Cg Dh Ei BfCg Dg Ei Ff Cg Dh Ei Ff Gg Dh Ei Ff Gg Hh 13
13 表7.2 二维输入的对应的元素形成 1 2 3 4 5 A B C D E B C D E F C D E F G D E F G H a b c d 1 Aa Bb Cc Dd Ea Bb Cc Dd Ea Fb Cc Dd Ea Fb Gc Dd Ea Fb Gc Hd e b c d 2 Ae Bb Cc Dd Ee Bb Cc Dd Ee Fb Cc Dd Ee Fb Gc Dd Ea Fb Ge Hd e f c d 3 Ae Bf Cc Dd Ee Bf Cc Dd Ee Ff Cc Dd Ee Ff Gc Dd Ee Ff Gc Hd e f g d 4 Ae Bf Cg Dd Ee Bf Cg Dd Ee Ff Cg Dd Ee Ff Gg Dd Ee Ff Gg Hd e f g h 5 Ae Bf Cg Dh Ee Bf Cg Dh Ee Ff Cg Dh Ee Ff Gg Dh Ee Ff Gg Hh i f g h 6 Ai Bf Cg Dh Ei Bf Cg Dg Ei Ff Cg Dh Ei Ff Gg Dh Ei Ff Gg Hh

如果S=5,S,=3,则4由As=E,F,G,H川和A3=ef,c,d对 应的元素形成,所以对于S=(5,3,A=E,f,Gc,Hd.用汉 明距H泛化能力,并表示为: H,=M-4入4 (7.3) 式中A为相交的符号。例如输入向量S=(2,4)→S-(2,6) 之间的汉明距为 H=4-Ee,Bf,Cg,Dd A Ei,Bf,Cg,Dh=2 (7.4) 从而可知,在M选定的情况下,汉明距愈小,说明两个 集合之间相交的愈多。 14
14 * * H M A A ij i j = − (7.3) 式中 为相交的符号。例如输入向量 之间的汉明距为 1 1 S S = → − (2,4) (2,6)) 12 H Ee Bf Cg Dd Ei Bf Cg Dh = − = 4 , , , , , , 2 (7.4) 如果 ,则 由 和 对 应的元素形成,所以对于 , .用汉 明距 泛化能力,并表示为: 1 2 S S = = 5, 3 A* 15 A E F G H = , , , 23 A e f c d = , , , S =(5,3) * A Ee Ff Gc Hd = ,,, Hij 从而可知,在M选定的情况下,汉明距愈小,说明两个 集合之间相交的愈多

个网络的知识描述,即权值(矩阵) 权值计算就是权值学习训练过程。CMAC网经过 映射g:A→P后,即把表4.3的元素经泛化处理后存放在联想 单元中,对上例表4.3中(5*6*4)的120个元素经泛化处理后仅 剩下18个。 即:表2中只有18个元素是不相同的。然后把这18个元素按 时S,嵌套在S,内的变化的规律存放在P的联想单元中作为地 址。每个地址对应一个权值。 15
15 一个网络的知识描述,即权值(矩阵) 权 值 计 算 就 是 权 值 学 习 训 练 过 程 。 CMAC 网经过 映射 后,即把表4.3的元素经泛化处理后存放在联想 单元中,对上例表4.3中(5*6*4)的120个元素经泛化处理后仅 剩下18个。 即:表2中只有18个元素是不相同的。然后把这18个元素按 时 嵌套在 内的变化的规律存放在P的联想单元中作为地 址。每个地址对应一个权值。 g A P : → 2 S 1 S