
数理统计中常用的分布除正态分布外,还有 三个非常有用的连续型分布,即 X2分布 t分布 数理统计的三大分布(都是连续型). F分布 它们都与正态分布有密切的联系 在本章中特别要求掌握对正态分布、X分布、 分布、F分布的一些结论的熟练运用.它们 是后面各章的基础
数理统计中常用的分布除正态分布外,还有 三个非常有用的连续型分布,即 χ 2分布 t分布 F分布 ⎫ ⎬ ⎭数理统计的三大分布 (都是连续型 ). 它们都与正态分布有密切的联系. 在本章中特别要求掌握对正态分布 、 χ 2分布 、 t分布 、 F分布的一些结论的熟练运用. 它们 是后面各章的基础

一分布 定义:设总体X~N(0,1),(X1,X2,,X)是X 的一个样本,则称统计量=X?+X?++X7服从自 由度为n的X2分布,记作x2~x(n) 自由度是指独立随机变量的个数,df=n x(n)分布的密度函数为 f0-=2T(m22-e ,y≥0 I(n+1)=n! 0, y<0
2 χ ——分布 定义 设总体,是 X N ~ 0,1 ( ) 的一个样本, 则称统计量 服从自 由度为n的 分布,记作 ( X1 2 , ,..., X Xn ) X 2 22 2 χ = + ++ X1 2 X X L n 2 χ 2 2 χ χ ~ () n 自由度是指独立随机变量的个数,df n = 2 χ ( ) n 分布的密度函数为 ( ) 21 2 2 1 , 0 ( ) 2 2 0, 0 n y n ye y f y n y ⎧ − − ≥ ⎪ = ⎨ Γ ⎪⎩ < Γ( 1) ! n n + =
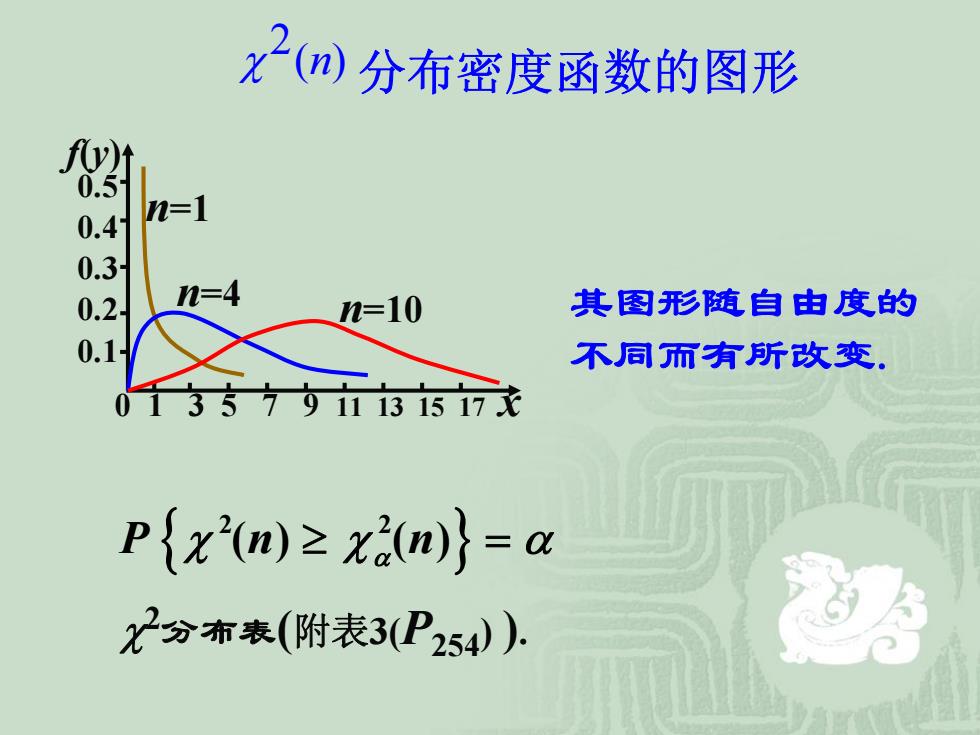
x2(m)分布密度函数的图形 n=1 0.2 n=4 n=10 其图形随自由度的 0.1 不同而有所改变。 357911131517 P{x2(m)≥xm)}=a 分布表(附表3(P254):
0 1 3 5 7 9 11 13 15 17 x 0.5 0.4 0.3 0.2 0.1 n=1 n=4 n=10 f(y) 其图形随自由度的 不同而有所改变. χ2分布表(附表3(P254) ). { } 2 2 Pn n () () χ ≥ = χ α α 分布密度函数的图形 2 χ ( ) n
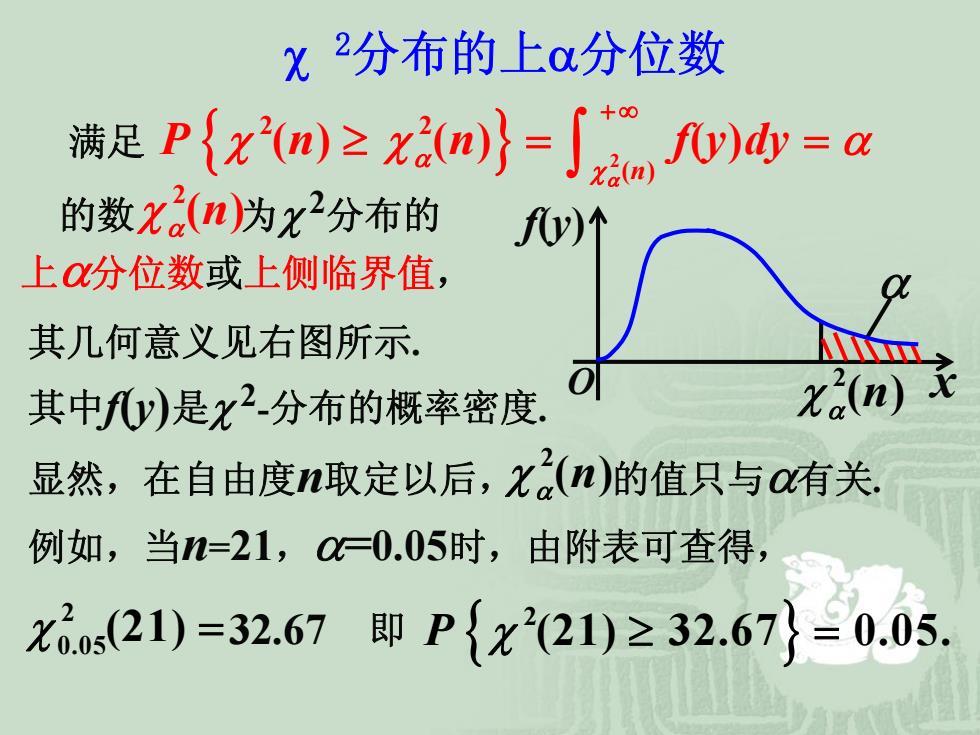
X分布的上分位数 满是P{xw≥2n=∫a心=a 的数x(n)为x2分布的 y)个 上分位数或上侧临界值, 其几何意义见右图所示 其中fy)是x2分布的概率密度. to(n)x 显然,在自由度n取定以后,x.(n)的值只与o有关, 例如,当=21,0=0.05时,由附表可查得, xs(21)=32.67即P{x2(21)≥32.67}=0.05
满足 { } 2 2 2 () ( ) ( ) () n P n n f y dy α α χ χ χ α + ∞ ≥= = ∫ 的数 为χ2分布的 上α分位数或上侧临界值, 2 χ α( ) n 其中f(y)是χ2-分布的概率密度. 其几何意义见右图所示. f(y) O x α 2 χ α( ) n 显然,在自由度n取定以后, 的值只与α有关. 2 χ α( ) n 例如,当n=21,α=0.05时,由附表可查得, 2 0.05 χ (21) =32.67 即 { } 2 P χ (21) 32.67 0.05. ≥ = χ 2分布的上α分位数
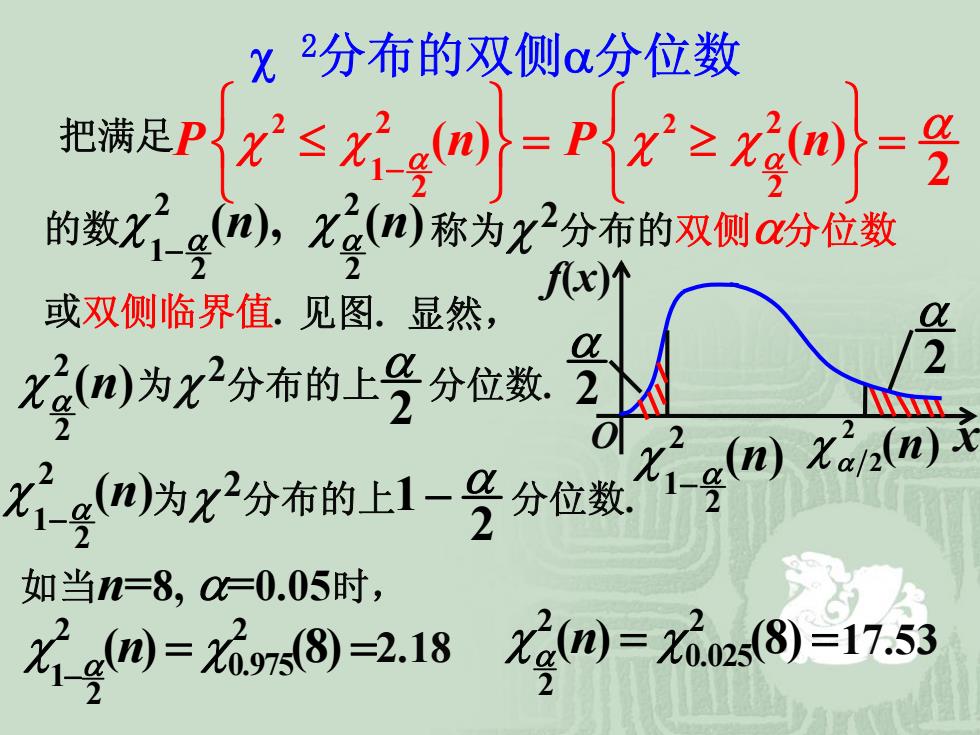
X2分布的双侧α分位数 把满足P父≤公gmP2≥含m 的数Xgn,Xgnj称为x2分布的双侧a分位数 fx)个 或双侧临界值.见图.显然, 2 Xgm为X2分布的上号分位数 . Xgm为X2分布的上1-号分位数 如当n=8,0=0.05时, g例=7s8)=2.18 X2m=22s8)=17.53
χ 2分布的双侧 α分位数 把满足 2 2 2 2 1 2 2 ( ) ( ) 2 P nP n α α α χχ χχ − ⎧ ⎫⎧ ⎫ ⎨ ⎬⎨ ⎬ ≤ =≥ = ⎩ ⎭⎩ ⎭ 的数 2 2 1 2 2 χ χ α α ( ), ( ) n n − 称为 χ 2分布的双侧 α分位数 或双侧临界值 . 见图 . f(x ) O x 2 2 2 χ α ( ) n 1 2 χ α( ) n − 2 α 2 α 显然, 2 2 χ α( ) n 为 χ 2分布的上 分位数 . 2 α 2 1 2 χ α( ) n − 为 χ 2分布的上 分位数 1 . 2 α − 如当 n =8, α=0.05时, 2 2 0.975 1 2 χ χ α( ) (8) n − = = 2 2 0.025 2 2.18 χ χ α( ) (8) n = =17.53