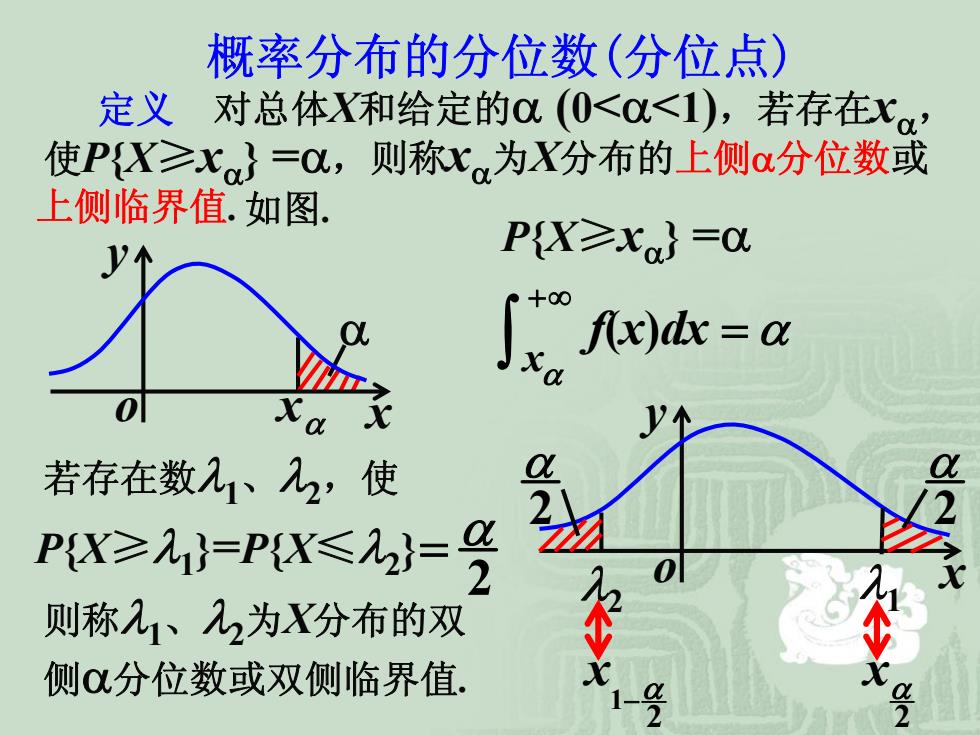
概率分布的分位数(分位点) 定义 对总体X和给定的0(0<0<1),若存在x。, 使P{X≥x}=C,则称x为X分布的上侧a分位数或 上侧临界值.如图. PX≥X}=0 -a 0 xa x 若存在数九、几2,使 2 PA,P≤=号 则称入1、入2为X分布的双 侧分位数或双侧临界值
概率分布的分位数(分位点) 使 P {X ≥ x α} = α , 定义 对总体X和给定的 α ( 0 < α < 1 ),若存在x α , 则称x α 为 X分布的上侧 α分位数 或 上侧临界值. 如图 . α o x α y x P {X ≥ x α} = α ( ) x f x dx α α + ∞ = ∫ 若存在数 λ1 、 λ2,使 P {X ≥ λ1 } =P {X ≤ λ2} 2 α = 则称 λ1 、 λ2 为 X分布的双 侧 α分位数或双侧临界值. o y λ x 2 λ1 2 α 2 α 1 2 x α − 2 x α

双侧α分位数或双侧临界值的特例 当X的分布关于y轴对称时,若存在七a/2,使 PX≥xa2}=aw, 则称xa2为X分布的双侧α分位数或双侧临界值. 如图. 2 2 ☑ a/2O
双侧α 分位数或双侧临界值的特例 2 PX x { }, ≥ = α α 则称 为X分布的双侧α分位数或双侧临界值. 当X的分布关于y轴对称时, 2 xα 如图. 2 x , 若存在 使 α y −xα 2 O xα 2 x 2 α 2 α
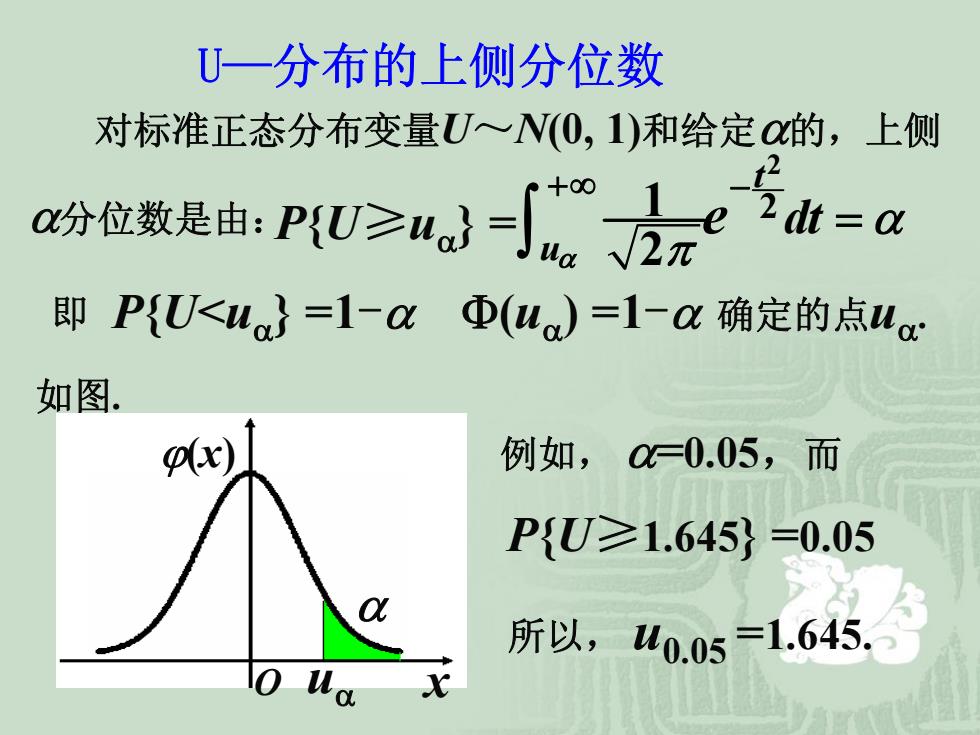
U一分布的上侧分位数 对标准正态分布变量U~N(0,1)和给定0的,上侧 a阶位数是由:PU≥,}2元e5h=a 即P{U<ua}=1-aΦ(ua)=1-a确定的点u 如图。 Ar) 例如,0=0.05,而 P{U≥1.645}=0.05 所以,40.05=1.645.5
U—分布的上侧分位数 对标准正态分布变量 U~ N(0, 1)和给定 α的,上侧 α分位数是由: P { U ≥ u α} = 2 1 2 2 t u e dt α α π +∞ − = ∫ P { U< u α} =1 - α Φ ( u α) =1 - α 确定的点 u α 即 . 如图 . ϕ(x ) O u α x α 例如, α=0.05 , 而 P { U ≥1.645} =0.05 所以, u0.05 =1.645
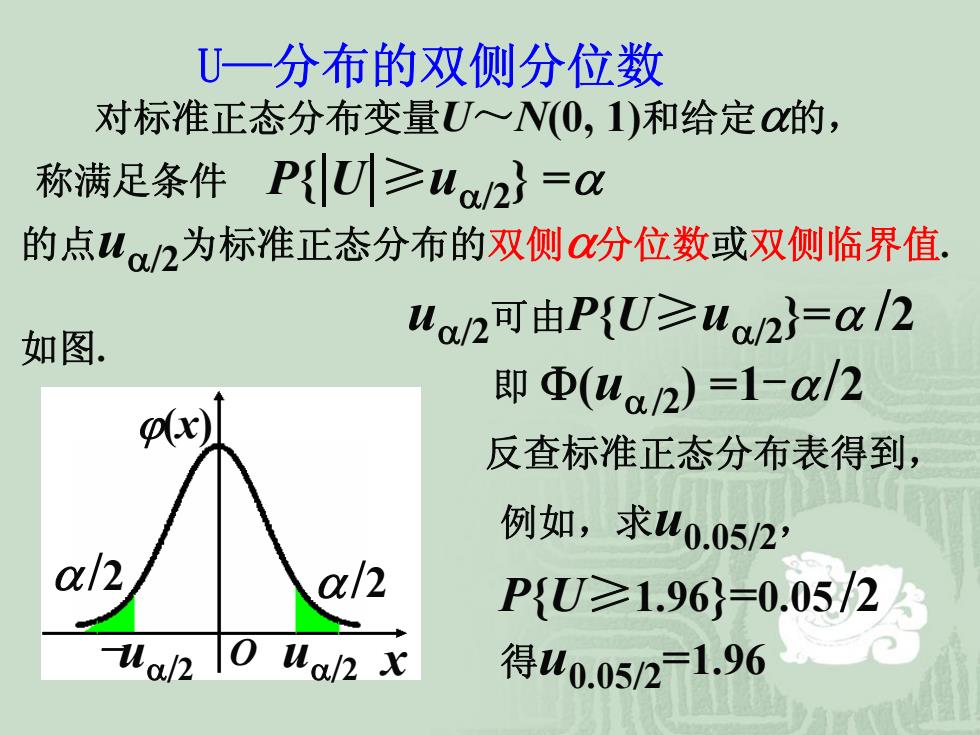
U一分布的双侧分位数 对标准正态分布变量U~N(0,1)和给定0的, 称满足条件PU≥u2}=C 的点u。2为标准正态分布的双侧a分位数或双侧临界值. 如图. ua2可由P{U≥u2}=a/2 即Φ(u2)=1-a/2 Ar) 反查标准正态分布表得到, 例如,求u0.05/2, 0/2 a/2 P{U≥1.96}=0.05/2 ual2 o ual x 得40.052=1.96
U—分布的双侧分位数 的点 u α / 2为标准正态分布的双侧 α分位数 或双侧临界值 . 如图 . u α / 2可由 P { U ≥ u α / 2}= α / 2 对标准正态分布变量 U~ N(0, 1)和给定 α的, 称满足条件 P {|U|≥ u α / 2} = α 即 Φ ( u α / 2) =1 - α/ 2 反查标准正态分布表得到, P { U ≥1.96}=0.05 / 2 例如,求 u0.05 / 2 , 得 u0.05 / 2 =1.96 ϕ(x ) O u α / 2 α/ 2 -u α / 2 α/ 2 x

标准正态分布的分位数 在实际问题中,0常取0.1、0.05、0.01. 常用到下面几个临界值: 40.05=1.645, 0.01=2.326 40.05/2=1.96, u0.01/2=2.575
标准正态分布的分位数 在实际问题中, α常取0.1 、0.05 、0.01 . 常用到下面几个临界值 : u0.05 =1.645 , u0.01 =2.326 u0.05 / 2 =1.96 , u0.01 / 2 =2.575