《经济数学基础》课程PPT教学课件（概率统计）第三章 多维随机变量及其分布 第4节 随机变量的独立性

第三章 随机变量及其分布 例1（续） §4随机变量的独立性 -{任aam9）(∈(o·+四)》 业4王任罩的本熟·电 y8cm足+am9） 3+aaeu{任+aaw9=5.6r6) X户人置粗耳师牙的饵企雪 合】返回主目录

例 1（续）  ( y(−， +) )      = + 10 arctan 2 1  y  所以，对于任意的实数x， y，有 ( )        +      = + 10 arctan 5 2 arctan 2 1 2 x y F x y    ，        +      = + 10 arctan 2 1 5 arctan 2 1 x  y    F (x)F (y) = X Y 所以X 与Y是相互独立的随机变量． 第三章 随机变量及其分布 §4随机变量的独立性 返回主目录

第三章 随机变量及其分布 离散型随机变量的独立性 §4随机变量的独立性 设(X,Y)是二维离散型随机变量，其联合分布律为 Py=PX=x Y=y （i,j=1,2,.） 又随机变量X的分布律为 P.=P{X=x,} (i=1,2,.) 随机变量Y的分布律为 P,=P{Y=y,} (j=1,2,.) 如果对于任意的i,j Pu=Pi.P. 则称X,Y是相互独立的随机变量. [合】返回主目录

离散型随机变量的独立性 设(X，Y)是二维离散型随机变量，其联合分布律为 pi j = PX = xi ， Y = y j  又随机变量X的分布律为 ( i，j =1， 2， ) pi = PX = xi  ( i =1， 2， ) 随机变量Y的分布律为 p j = PY = y j  ( j =1， 2， ) 如果对于任意的i， j pij = pi p j 则称X，Y是相互独立的随机变量． 第三章 随机变量及其分布 §4随机变量的独立性 返回主目录

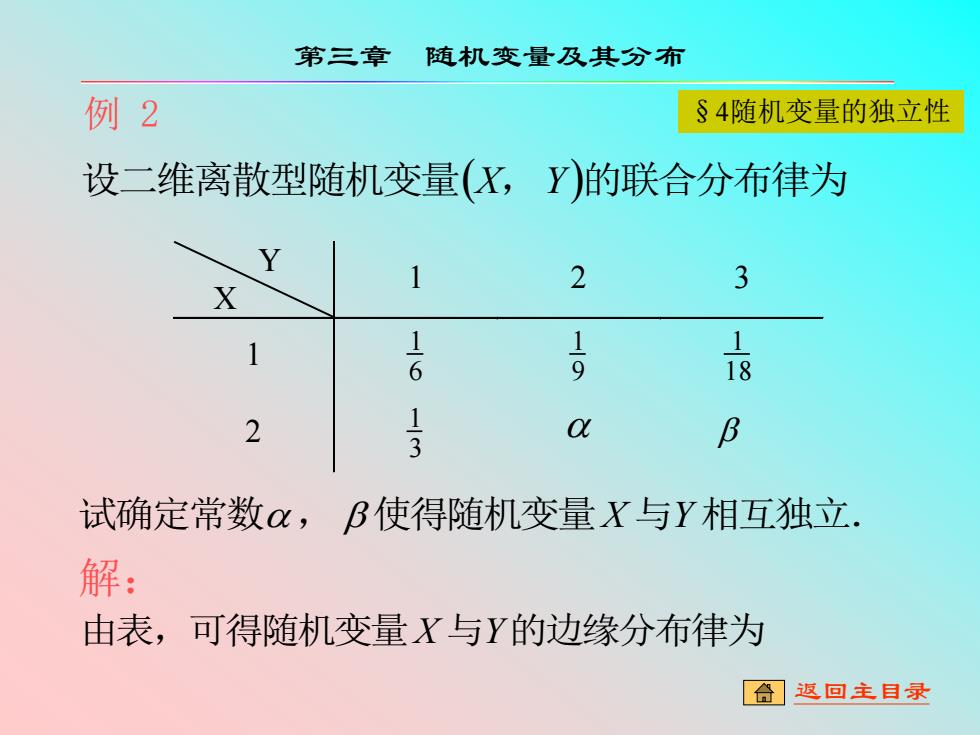
第三章 随机变量及其分布 例2 §4随机变量的独立性 设二维离散型随机变量(X,Y)的联合分布律为 Y 1 2 3 1 1-6 1-9 8 2 1-3 o B 试确定常数α，B使得随机变量X与Y相互独立. 解： 由表，可得随机变量X与Y的边缘分布律为 合】返回主目录

例 2 设二维离散型随机变量(X，Y)的联合分布律为 Y X 1 2 3 1 6 1 9 1 18 1 2 3 1   试确定常数，  使得随机变量X 与Y 相互独立． 解：由表，可得随机变量X 与Y的边缘分布律为 第三章 随机变量及其分布 §4随机变量的独立性 返回主目录

第三章 随机变量及其分布 例2（续） §4随机变量的独立性 Y 1 2 3 Pi 1 1-6 号 18 2 13 Ox B 3+a+B s+a 8+B 如果随机变量X与Y相互独立，则有 P=P.Py（i=1,2:j=1,2,3) 由此得 [合】返回主目录

例 2（续） Y X 1 2 3 pi 1 6 1 9 1 18 1 3 1 2 3 1   3 ++ 1 p j 2 1 1 9 + 18+ 1 如果随机变量X 与Y 相互独立，则有 pij = pi p j ( i =1， 2； j =1， 2，3) 由此得 第三章 随机变量及其分布 §4随机变量的独立性 返回主目录

第三章随机变量及其分布 例2（续） §4随机变量的独立性 -P(x=1 Y-2Px-2-(1a) 1 2 由此得 9 又由 x=1y-3}-Px=1y=3)ge 18 1 由此得 B= 9 ① 而当= B= 二时，联合分布律及边缘分布律为 合】返回主目录

例 2（续）  1 2  9 1 = P X = ， Y = 由此得 ； 9 2  = 又由  1 3 18 1 = P X = ， Y = 由此得 ． 9 1  =       =  + 9 1 3 1 = PX =1PY = 2       =  +  18 1 3 1 = PX =1PY = 3 而当 ， 时，联合分布律及边缘分布律为 9 1 9 2  =  = 第三章 随机变量及其分布 §4随机变量的独立性 返回主目录