
第二章 随机变量及其分布 ·随机变量 ·离散型随机变量的概率分布 ·随机变量的分布函数 ·连续型随机变量的概率密度 ·随机变量的函数的分布 合】返回主自录
• 离散型随机变量的概率分布 • 随机变量的分布函数 • 连续型随机变量的概率密度 • 随机变量的函数的分布 第二章 随机变量及其分布 • 随机变量 返回主目录

第二章 随机变量及其分布 §1随机变量 §1随机变量 一.随机变量的概念 例1 袋中有3只黑球,2只白球,从中任意取出3只球, 观察取出的3只球中的黑球的个数, 我们将3只黑球分别记作1,2,3号,2只白球分别 记作4,5号,则该试验的样本空间为 (1,2,3(1,2,4)(1,2,5) (1,3,4) (1,3,5) ,4,5) S= (2,3, 4) (2,3,5) (2,4,5) (3, 4, 5) 合】返回主目录
§1 随机变量 第二章 随机变量及其分布 一.随机变量的概念 例 1 袋中有3只黑球,2只白球,从中任意取出3只球, 观察取出的3只球中的黑球的个数. 我们将3只黑球分别记作1,2,3号,2只白球分别 记作4,5号,则该试验的样本空间为 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) = 3 4 5 2 3 4 2 3 5 2 4 5 1 3 4 1 3 5 1 4 5 1 2 3 1 2 4 1 2 5 , , , , , , , , , , , , , , , , , , , , S §1 随机变量 返回主目录

第二章 随机变量及其分布 §1随机变量 例1(续) 我们记取出的黑球数为X,则X的可能取值为1, 2,3. 因此,X是一个变量. 但是,X取什么值依赖于试验结果,即X的取值 带有随机性, 所以,我们称X为随机变量, X的取值情况可由下表给出: 合】返回主自录
例 1(续) 我们记取出的黑球数为 X,则 X 的可能取值为1, 2,3. 因此, X 是一个变量. 但是, X 取什么值依赖于试验结果,即 X的取值 带有随机性, 所以,我们称 X 为随机变量. X 的取值情况可由下表给出: 第二章 随机变量及其分布 §1 随机变量 返回主目录
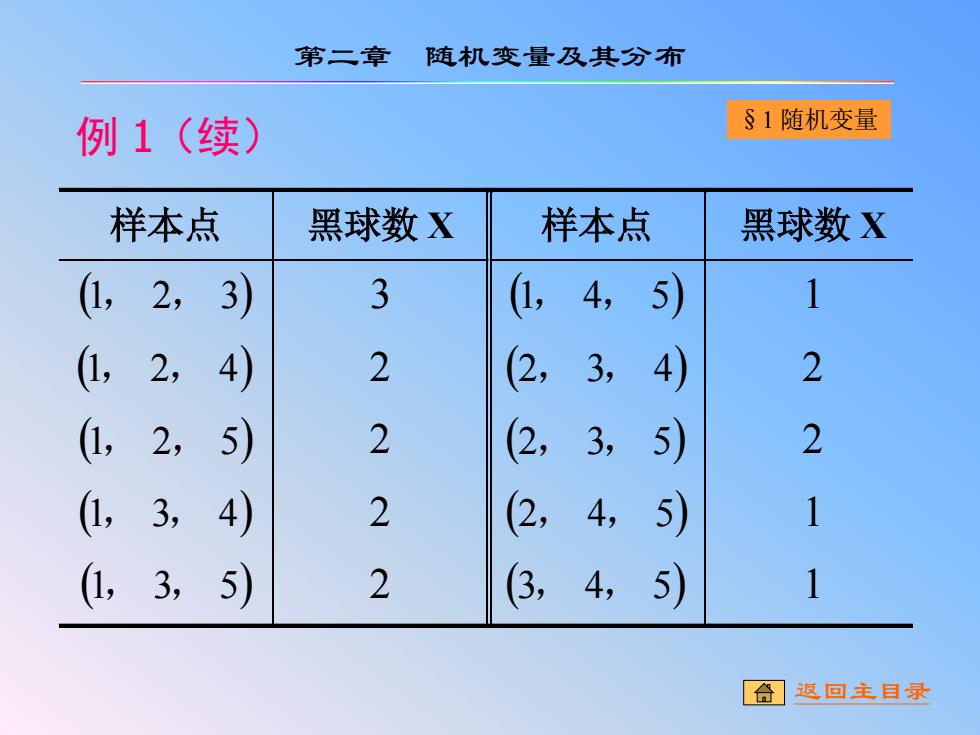
第二章 随机变量及其分布 例1(续) §1随机变量 样本点 黑球数X 样本点 黑球数X (1,2,3) 3 (1, 4, 5) 1 (1,2,4) 2 (2, 3, 4) 2 (1,2,5) 2 , 3, 5) 2 (1,3,4) 2 (2, 4,5) 1 (1,3,5) 2 (3, 4,5) 1 合】这回主目录
例 1(续) 样本点 黑球数 X 样本点 黑球数 X (1, 2, 3) 3 (1, 4, 5) 1 (1, 2, 4) 2 (2, 3, 4) 2 (1, 2, 5) 2 (2, 3, 5) 2 (1, 3, 4) 2 (2, 4, 5) 1 (1, 3, 5) 2 (3, 4, 5) 1 第二章 随机变量及其分布 §1 随机变量 返回主目录

第二章 随机变量及其分布 例1(续) §1随机变量 由上表可以看出,该随机试验的每一个结果都对应 着变量X的一个确定的取值,因此变量X是样本空 间S上的函数: =xe) (eeS) ·我们定义了随机变量后,就可以用随机变量的取 值情况来刻划随机事件.例如 {e:X(e)=2={x=2 表示取出2个黑球这一事件; {X≥2 表示至少取出2个黑球这一事件,等等 [合】返回主自录
由上表可以看出,该随机试验的每一个结果都对应 着变量 X 的一个确定的取值,因此变量 X 是样本空 间S上的函数: X = X(e ) (eS) • 我们定义了随机变量后,就可以用随机变量的取 值情况来刻划随机事件.例如 X 2 表示至少取出2个黑球这一事件,等等. 第二章 随机变量及其分布 例 1(续) §1 随机变量 e:X(e ) = 2=X = 2 表示取出2个黑球这一事件; 返回主目录