电子科技大学：《图像处理及应用 Image Processing and Application》课程教学资源（课件讲稿）Chapter 04 Filtering in the Frequency Domain

电子科发女学光电科学与工程学院 SCHOOL OF OPTOELECTRONIC SCIENCE AND ENGINEERING OF UESTC 4.Fourier Transform of Functions of One Continuous Variable Representation of Fourier transform in polar coordinates F(n）=|F(e四 Power spectrum P()=F()=R()+I2(u)

( ) ( ) j ( ) F F e     = ( ) ( ) ( ) ( ) 2 2 2 P F R I     = = + 4. Fourier Transform of Functions of One Continuous Variable ◼ Representation of Fourier transform in polar coordinates ◼ Power spectrum

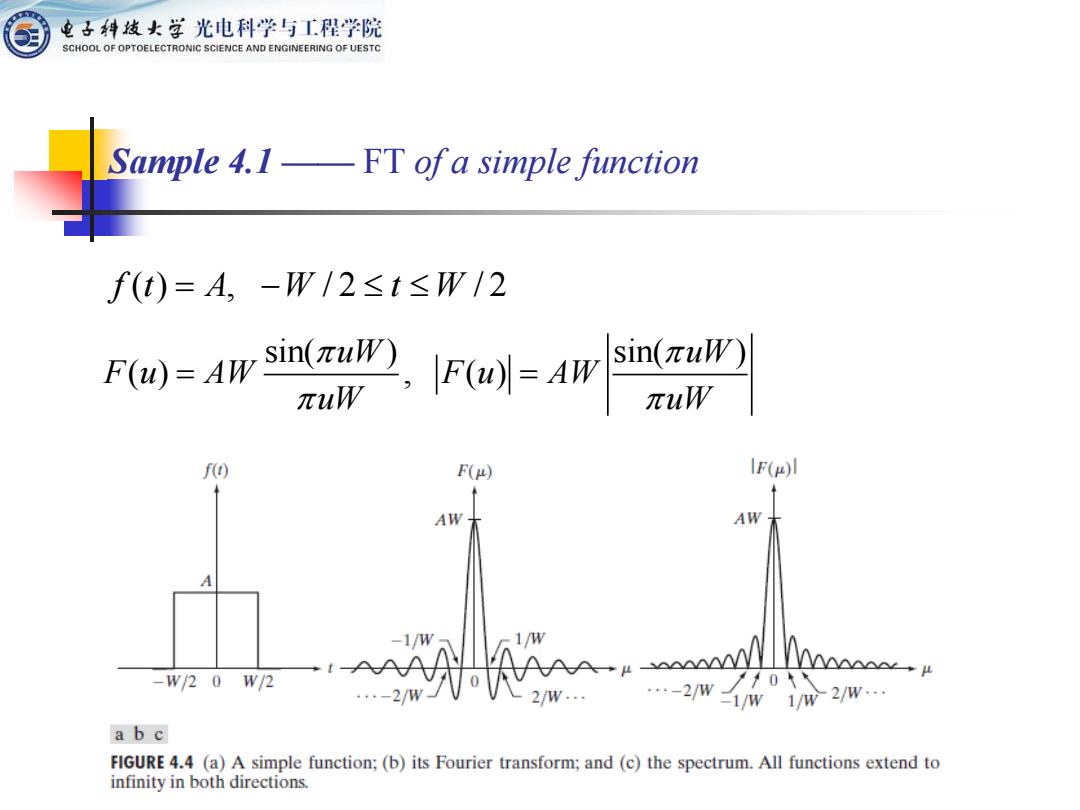
电子科发女学光电科学与工程学院 SCHOOL OF OPTOELECTRONIC SCIENCE AND ENGINEERING OF UESTC Sample 4.1-FT of a simple function f(t)=A,-W/2≤t≤W/2 F(u)=AWS w.a-4 πu f(t) F() IF() AW AW 7 -1/W -w/20w/2 -2m02w ab c FIGURE 4.4 (a)A simple function;(b)its Fourier transform;and(c)the spectrum.All functions extend to infinity in both directions

Sample 4.1 —— FT of a simple function f t A W t W ( ) , / 2 / 2 = −   sin( ) sin( ) ( ) , ( ) uW uW F u AW F u AW uW uW     = =

电子科发女学光电科学与工程学院 SCHOOL OF OPTOELECTRONIC SCIENCE AND ENGINEERING OF UESTC Sample 4.2-FT of impulse and impulse train t-0,impulse F(u)=6)e2di=∫re2wδ(0)dt=e20=e°=l t-to impulse F(u)=(t-t)e pudi=e(t-to)di=e cos(2mt)-jsin(2t)

Sample 4.2 —— FT of impulse and impulse train ( ) ( ) ( ) 2 2 0 2 0 1 j t j t j F t e dt e t dt e e       + + − − − −  − = = = = =   ( ) ( ) ( ) ( ) ( ) 0 0 0 2 2 2 0 0 cos 2 sin 2 j t j t j t F t t e dt e t t dt t j t e         + + − − − − − = − = − = = −   ◼ t=0, impulse ◼ t=t0 , impulse

电子科发女学光电科学与工程学院 SCHOOL OF OPTOELECTRONIC SCIENCE AND ENGINEERING OF UESTC Sample 4.2-FT of impulse and impulse train impulse train w=2ce品 2πn 2πn 502e0 s例-收w-s位合-点合2品

Sample 4.2 —— FT of impulse and impulse train ◼ impulse train ( )  ( ) 2 2 1 1 1 n n j t j t T T T n n n n S s t e e T T T T            =− =− =−       =  =  =  = −                    ( ) ( ) ( ) ( ) 2 2 2 2 2 0 2 2 2 , 1 1 1 1 1 n j t T T n n n n T T j t j t T T n T T T n j t T T n s t c e c s t e dt t e dt e T T T T s t e T         =−   − −  − −    =− = = = = =     =     

电子科发女学光电科学与工程学院 SCHOOL OF OPTOELECTRONIC SCIENCE AND ENGINEERING OF UESTC 5.Convolution Definition f(t)*h()=f()h(t-z)dr and FT 3()h(()h(-)drnd =∫fh-)e2h: =f(lH(We2rr=H(四F(四 Convolution theorem f(t)*h(t)台F()H() f(t)h(t)台F()*H()

f t h t f h t d ( ) * ( ) (   ) ( ) + − = −  ◼ Definition and FT ◼ Convolution theorem 5. Convolution  ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 2 2 * j t j t j f t h t f h t d e dt f h t e dt d f H e d H F                 − − −   − − −  − −    = −       = −     = =     