
北京邮电大学工学博士学位论文 当神经脉冲向周围散去,K+离子通道开始打开,并允许带正电的K+离子流出 细胞外,在这个过程,等于又将负电荷搬入了细胞膜内,于是,电压下降,细胞膜被 认为是再极化状态(repolarize state),因为细胞膜又回到了“外正内负”的状态。这 种神经元去极化和再极化的过程,称为动作电位或者神经冲动。 在神经冲动以后,由于电压门控飞+离子通道仍然打开,导致+离子继续流出 细胞膜外,这就导致细胞膜上的电压略低于静息电位电压,此时细胞膜处于超级化 状态(hyperpolarized state),在这个时间段内,神经元处于不应期(refractory period) 状态,并且持续的时间非常短暂,这时细胞膜上的N+离子流出到细胞外,K+离子 回到细胞内,因此回到了静息状态。总的来说,神经元的动作电位是一系列的电压 门控离子通道开启和关闭的过程。动作电位的产生,离子的跨膜流动,促使神经元 产生电信号,所以动作电位是神经信息的载体。 2.1.3神经突触 神经元之间是通过突触(synapse)相互连接,用神经递质(neurotransmitter)进行 神经信号传递,以实现神经元细胞间的信息交流。大脑神经元之间的信号传输也是通 过复杂的突触结构来完成的。突触既是生物神经元相互关联的结构,也是信号在生 物脑内传输的重要环节。如图24所示为典型的突触结构③。化学突触是脊椎动物大 图2-4神经元突触的结构示意图 14 (C)1994-2021 China Academic Joumal Electronic Publishing House.All rights reserved.http:/www.cnki.net
北 京 邮 电 大 学 工 学 博士 学 位 论文 当 神 经脉冲 向 周 围 散去 , 欠 + 离子 通道开始 打开 , 并允许带正 电 的 尤+ 离 子流 出 细 胞 外 , 在这个过程 , 等于又将 负 电 荷搬入 了 细 胞膜 内 , 于是 , 电 压下 降 , 细 胞膜被 认为 是再极化状态 ( r ep o l a ri z e s t at e ) , 因 为 细胞膜又 回 到 了 “ 外正 内 负 ” 的 状态 。 这 种 神 经元去极化 和 再极化 的 过程 , 称为 动作 电 位或者神 经 冲 动 。 在神 经 冲 动 以 后 , 由 于 电 压 门 控 欠+ 离子通道仍 然打开 , 导致 尤+ 离子继续流 出 细 胞膜 外 , 这就导致细 胞 膜上 的 电 压略 低于静 息 电 位 电 压 , 此 时 细 胞膜 处 于 超级 化 状态 ( h y p e rp o l a r i z e d s t at e ) , 在这个 时 间 段 内 , 神经元处于不 应期 ( r e fr a c t o ry p e r i o d ) 状态 , 并且持续 的 时 间 非常短暂 , 这时 细 胞膜上 的 离子流 出 到 细 胞 外 , 尤 + 离子 回 到 细 胞 内 , 因 此 回 到 了 静 息 状态 。 总 的 来说 , 神 经 元 的 动作 电 位 是 一 系 列 的 电 压 门 控 离子通 道开 启 和 关 闭 的 过程 。 动作 电 位 的 产生 , 离 子 的 跨膜 流动 , 促使 神 经元 产生 电信号 , 所 以 动作 电 位是神 经信息 的 载体 。 2 . 1 . 3 神 经 突 触 神经 兀 之 间 是 通过 突 触 ( s y n a p s e ) 相 互连接 , 用 神 经递 质 ( n e u r o t r a n s mi te r ) 进 行 神 经 信号传递 , 以 实 现神 经元 细 胞 间 的 信息交流 。 大脑 神 经 元之 间 的 信号传输也是通 过 复 杂 的 突触结 构来 完 成 的 。 突触 既是 生 物 神 经元 相 互关联 的 结 构 , 也是 信号在 生 物 脑 内 传输 的 重要环节 。 如 图 2 - 4 所示 为 典型 的 突触结构? 。 化 学 突 触是脊 椎 动物大 P r e s y na pt i c n e u r o n — j馨一 汄 ' ^ ^、 、 %, ^4 / / \ / A x o n t e r m i n a l / < V ; ; ? / ; 、 , ,' 、 ' v 、 ' 、 S y n a p t c ’ v e s i c ' e s N e u r o l r a n s mi t t e r s x x ; . S y n a p t s c L i g a n d - g a t e d c h a n n e l s 一_ c l e f t w i t h r e c e p t o r s f o r \ ^ n e u r o l r a n s m i t e r s ^ 图 2 - 4 神 经 元 突 触 的 结 构 示 意 图 1 4

第二章基本知识和基本概念 脑中最常见的突触类型。当突触前神经元产生兴奋,动作电位沿着细胞膜传到轴突 末端,引起细胞膜内外离子流动,它会触发突触前膜释放神经递质(neurotransmitter) 到突触间隙。当神经递质到达突触后神经元时,它们将与突触后神经元细胞膜上的 特异受体结合,并引导(直接或通过生化信号链)突触后膜打开特定的离子通道,使 细胞外液的离子流入细胞内。离子流入反过来改变突触后部位的膜电位,最终,化 学信号被转化为电反应,引起突触后神经元兴奋或者抑制。突触后神经元对突触前 尖蜂的电压响应称为突触后电位。除了化学突触,神经元也可以通过电突触(有时被 称为间隙连接)耦合。 神经元有多种不同的分类方式,根据神经元的耦合机制,突触可以划分为电突 触和化学突触两种类型,再按突触后神经元的响应特性又可以分为兴奋型和抑制型。 兴奋性突触后电位(EPSP):动作电位传至轴突末梢引起突触前膜释放兴奋性神 经递质,与突触后膜受体结合,突触后膜对N+离子和K+离子的通透性增强,从 而使突触后膜去极化,产生EPSP,通过EPSP累积引发动作电位。 抑制性突触后电位(PSP):动作电位传至轴突末梢引起突触前膜释放抑制性神 经递质,这些神经递质经过突触间隙的扩散与突触后膜受体结合,突触后膜对K+离 子和C~离子(主要对C离子)的通透性提高,引起突触后膜超极化,产生IPSP。 本研究中也对兴奋性和抑制性神经元的动力学特性进行了深入的讨论,将在后文中 具体介绍。 2.2计算神经科学模型及其动力学 人类对脑神经系统的研究源远流长,最早可以追溯到Waldycr于1891年提出的 神经元学说[5),它将细胞学说的观点应用于神经元并将其具体化。此后,意大利解 剖学家Gog在1873年通过镀银法可以显示出神经元的全貌,人们对神经元的认识 又前进了一大步。与此同时,西班牙的解剖学家Cajl通过大量的生物实验对之前的 方法进行了改进。百余年来,随着科学技术的不断进步,计算机和人工智能的发展 信息技术产业已经成为了现代经济的重心,经过几代科学家们的不断努力,计算神经 科学作为脑科学中跨领域的交叉学科逐步推动了人类对大脑的探索。它是一门集生 物,医学,统计学,物理学和计算机信息科学为一体的交叉学科,在计算神经科学领 域,为了模拟生物神经元的动作电位,众多学者进行了不断的探索。Hodgkin-Huxley ③图片来源于:hitp:/.baidu.com/item/突触前部2223895S C)199-01China Academie Joumal Electronic Publishing House.All rights reserved.http://www.nk
第 二章 基本知 i只 和 基本概 念 脑 中 最 常 见 的 突 触 类型 。 当 突触前神 经 元产生 兴奋 , 动 作 电 位沿着细 胞膜传到 轴 突 末端 , 引 起细 胞膜 内 外离子流动 , 它 会触发 突触前膜释放神经递质 ( ne uro trans mi tt e r ) 到 突触 间 隙 。 当 神 经递质到 达突触后神 经元 时 , 它 们 将与 突触后神经元细 胞膜上 的 特异 受 体结合 , 并 引 导 ( 直接或 通过生化 信号链) 突触后膜打开特定 的 离子通道 , 使 细 胞 外液 的 离子 流入细 胞 内 。 离子流入反 过来 改 变突 触后部位 的 膜 电 位 , 最终 , 化 学信号 被转化 为 电 反应 , 引 起突触后 神 经元兴 奋或者抑 制 。 突触 后神 经 元对突触前 尖峰 的 电压响 应称为突 触后 电位 。 除 了 化学 突触 , 神经元也可 以 通过 电 突触 ( 有时被 称为 间 隙连接) 耦合 。 神 经元 有 多 种不 同 的 分 类方式 , 根据神 经元 的 耦合机制 , 突触可 以 划 分 为 电突 触和 化 学突触两种 类型 , 再按 突触后神经元 的 响 应特性又可 以 分为 兴奋型和抑 制 型 。 兴奋性突触后 电 位 ( EP S P ) : 动作 电 位传至轴 突末梢 引 起 突触前膜释放兴奋性神 经递质 , 与突 触后膜受 体结 合 , 突触 后膜对 离子和 离子 的 通透性 增 强 , 从 而使突触后膜去极化 , 产生 EP S P , 通过 EP S P 累 积引 发 动作 电位 。 抑 制 性突触 后 电位 ( I P S P ) : 动作 电 位传至轴 突末 梢 引 起突触前膜释放抑制 性神 经递质 , 这些 神经递质 经过突触 间 隙 的 扩散与突触 后膜受体结合 , 突 触后膜对 欠 + 离 子和 C/ _ 离子 ( 主要对 C/ _ 离子 ) 的通透性 提高 , 引 起突触后 膜超极化 , 产生 I P S P 。 本研究 中 也对兴奋性和 抑 制性 神经元 的 动 力 学 特性进行 了 深入 的 讨论 , 将在后文 中 具体介 绍 。 2 . 2 计算神 经科 学 模型及 其 动 力 学 人类对脑神 经 系 统 的 研究源远流长 , 最早可 以 追溯 到 Wa l dy c r 于 1 8 9 1 年提 出 的 神 经元学说 [ 5 5 ] , 它 将细 胞学说 的 观点 应 用 于神经元并将其具体化 。 此后 , 意大利 解 剖学 家 Go l g i 在 1 8 7 3 年通过镀银法 可 以 显示 出 神 经元 的 全貌 , 人 们对神经 元 的 认识 又前进了 一 大步 。 与此 同 时 , 西班牙 的 解剖学 家 C aj al 通过大量 的 生物实验对之前的 方法进行了 改 进 。 百 余 年来 , 随着科学技术 的 不 断进步 , 计算机和 人工智 能 的 发展 , 信息技术产业 已 经 成 为 了 现代经济 的 重心 , 经过几代科学 家 们 的 不 断努力 , 计算神经 科学 作为脑科学 中 跨领域 的 交叉学科逐 步推 动 了 人类对大脑 的 探索 。 它 是一 门 集生 物 , 医 学 , 统计学 , 物理学和 计算机信息科学为 一 体的 交叉学 科 , 在计算神经科学领 域 , 为 了 模拟生物神经 元 的 动作 电位 , 众多 学者进行了 不断 的 探索 。 Ho dgki n- Huxl e y ③ 图 片 来源 f : htp s : / / b a i k e . b a i d u . c o m/ i t e m/ 突 触 前部/ 2 2 2 3 8 9 5 3 1 5

北京邮电大学工学博士学位论文 神经元模型的提出为计算神经科学领域开辟了新的方向,可以通过数学的角度对神 经元的放电行为进行模拟[S,接下来Hindmarsh-Rose神经元模型提出了比较简化的 表达方式,同时在数值计算和计算机模拟上提高了性能57。直到21世纪初期,二 维的Izhikevich神经元模型的提出大力促进了神经元在复杂大规模集群网络上的研 究5。 在这一节中,主要对本课题所涉及的数学模型和相关知识进行阐述。 2.21 Hodgkin-Huxley神经元模型 从生物学的观点来看,动作电位是通过细胞膜离子通道产生电流的结果。基于 神经元动作电位的动态特性,神经科学家们建立了许多数学模型,它们是构成神经 网络的基本单元,为深入研究神经网络的动力学特性奠定了基础。二十世纪四十年 代,Alan Hodgkin和Andrew Huxley阐明了神经细胞产生动作电位的基本物理机制。 他们在乌贼的巨轴突上进行了一系列广泛的实验,通过对电位数据的分析整理,提 出了一组由微分方程表示的数学模型以及对应的电路模拟,描述了神经元动作电位 的动力学机制[5阿。这个工作发表于1952年,完美的将生物实验结果与优雅的数学理 论相结合,并最终为霍奇金和赫胥黎在1963年获得了诺贝尔奖。可以说这是迄今为 止在神经科学领域最具影响力的论文,并为计算神经科学和人工智能领域的发展奠 定了基础。经典的Hodgkin-Huxley神经元模型可以由以下四个微分方程来表示: =8Nomh(Vxa-V)+8xn'(Vx-V)+&L(VL-V)+1. (2-1) dm =an(V1-m-B(W)m (2-2) =(V)(1-h)-B,(V)h, (2-3) 加出 =an(V)(1-n)-B.(V)n(V) (2-4) 其中a和B满足如下条件: (W+40)/10 a.W]=1-exp-V+40/10,BW))=4ep(-V+61/18, a4W)=007exp(-(V+65/20,mW)=1+ep(-V+35j/o (2-5) 0.01(W+55) (V)=1-exp(-(V+5)/10)' Bn(W)=0.125exp(-(V+65)/80). 16 (C)1994-2021 China Academie Joumal Electronic Publishing House.All rights reserved.http://www.cnki.net
北京 邮 电大学 工 学博士 学 位 论文 神经元模型 的 提 出 为 计算神 经科学领域开 辟 了 新 的 方 向 , 可 以 通过数学 的 角 度对神 经元 的放 电行为进行模拟 [ 5 6 ] , 接下来 Hi ndmar s h- Ro s e 神经元模型提 出 了 比较简化 的 表达方式 , 同 时在数值计算和 计算机模拟 上提 高 了 性 能 [ 5 7 ] 。 直 到 2 1 世 纪初 期 , 二 维 的 I zhi kev i c h 神 经 元模型 的 提 出 大 力 促进 了 神 经 元在复杂 大规模集群 网 络上 的 研 究 [ 5 8 ] 。 在这一 节 中 , 主要对本课题所涉及 的 数学模型和相关知 识进行 阐 述 。 2 . 2 . 1 Ho d gki n- Huxl ey 神 经 元模型 从生 物 学 的 观点 来看 , 动 作 电 位是通 过细 胞膜离子通道产生 电 流 的 结果 。 基于 神经 元动 作 电 位 的 动 态特性 , 神 经科学 家 们 建立了 许多 数学 模型 , 它 们 是构 成 神 经 网 络 的 基本单元 , 为 深入研究 神经 网 络 的 动 力 学 特性 奠定 了 基础 。 二十世纪 四 十年 代 , Al an Ho dgki n 和 Andr e w Huxl e y 阐 明 了 神 经 细 胞产生动 作 电 位 的 基本物 理机制 。 他们在乌 贼 的 巨 轴 突 上进行 了 一 系 列 广 泛 的 实验 , 通过对 电 位数据 的 分析整理 , 提 出 了 一 组 由 微分方程表示 的 数学模型 以 及对应 的 电 路模拟 , 描述了 神经 元动 作 电位 的 动 力 学 机制 [ 5 6 ] 。 这个工作 发表于 1 9 5 2 年 , 完美 的 将生物 实验结果与优雅 的 数学理 论相结合 , 并最终为 霍奇金和 赫胥黎在 1 9 6 3 年获得 了 诺贝 尔 奖 。 可 以说这是迄今为 止在神经科学领域最具影 响 力 的 论文 , 并 为计算神 经科学和 人工 智 能 领域 的 发展奠 定 了 基础 。 经典的 Ho d gki n-Huxl ey 神 经兀模型可 以 由 以下 四 个微分方程来表7K : ?”4 ( 心 — V ) + 豇 ㈧ - V ) + / , ( 2 - 1 )  ̄ m )  ̄ ^nSy ) m i ( 2 - 2 ) dh — = a/ i ( V ' ) ( l — h ) - ^h ( V ) h , ( 2 - 3 ) — = a? ( V ) ( l — n ) - j 5? ( V ) n ( V ) , ( 2 - 4) 其 中 a 和 满足如 下条件 : = 副 = 4-( — ( 嘴】 8 ) , ah ( V ) = 0 . 07 eXp ( - ( V + 6 5 ) / 20 ) , ,卜 】 + 一:“ . 司周 , ( 2 - 5 ) _ = 綱 , 副 ―p ( - ( V + 6 5 ) / 8 〇 ) . 1 6
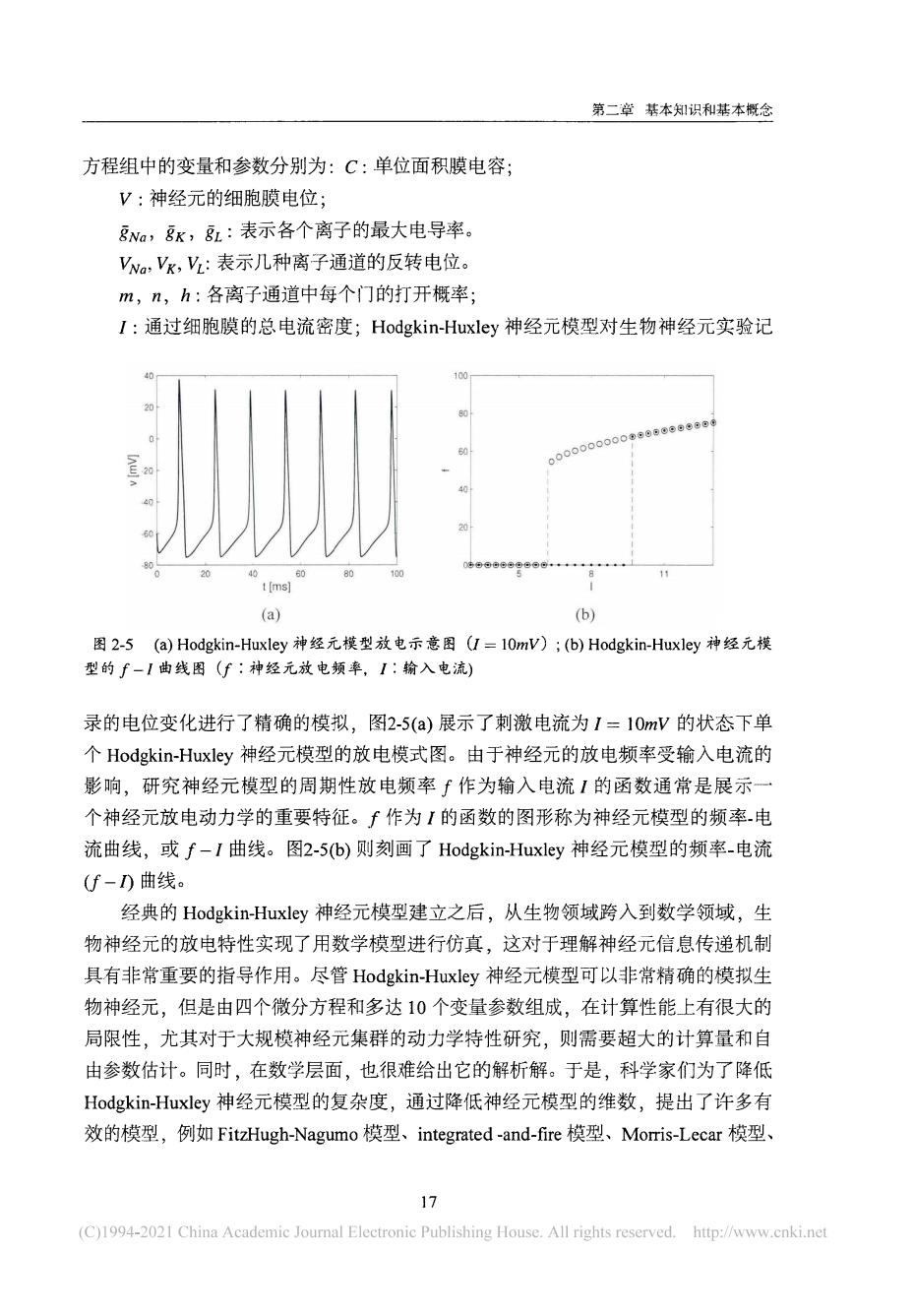
第二章基本识利和基本概念 方程组中的变量和参数分别为:C:单位面积膜电容; V:神经元的细胞膜电位; Na,K,:表示各个离子的最大电导率。 Va,Vk,2:表示几种离子通道的反转电位。 m,n,h:各离子通道中每个门的打开概率; I:通过细胞膜的总电流密度;Hodgkin-Huxley神经元模型对生物神经元实验记 .09 (a) (b) 图2-5(a)Hodgkin-HuxIey神经元模型放电示意图U=10mW):(b)Hodgkin-Huxley神经元模 型的f一I曲线图(f:种经元放电频率,1:输入电流) 录的电位变化进行了精确的模拟,图2-5(a)展示了刺激电流为I=10mV的状态下单 个Hodgkin-Huxley神经元模型的放电模式图。由于神经元的放电频率受输入电流的 影响,研究神经元模型的周期性放电频率∫作为输入电流1的函数通常是展示 个神经元放电动力学的重要特征。∫作为【的函数的图形称为神经元模型的频率电 流曲线,或f-I曲线。图2-5(b)则刻画了Hodgkin-Huxley神经元模型的频率-电流 (f-D曲线。 经典的Hodgkin-Huxley神经元模型建立之后,从生物领域跨入到数学领域,生 物神经元的放电特性实现了用数学模型进行仿真,这对于理解神经元信息传递机制 具有非常重要的指导作用。尽管Hodgkin-Huxley神经元模型可以非常精确的模拟生 物神经元,但是由四个微分方程和多达10个变量参数组成,在计算性能上有很大的 局限性,尤其对于大规模神经元集群的动力学特性研究,则需要超大的计算量和自 由参数估计。同时,在数学层面,也很难给出它的解析解。于是,科学家们为了降低 Hodgkin-Huxley神经元模型的复杂度,通过降低神经元模型的维数,提出了许多有 效的模型,例如FitzHugh-Nagumo模型、integrated-and-fire模型、Momris-Lecar模型、 1 C)1994-201China Academie Joumal Electronic Publishing House.All rights reserved.http://www.cnke
第 二章 基本 知 识 和 基 本 概 念 方程组 中 的 变量和 参数分别 为 : C : 单位面积膜 电 容 ; V : 神 经元 的 细胞膜 电 位 ; k , 表示 各个离子 的 最大 电 导率 。 表示几 种离子通道 的 反转 电 位 。 m , 《 , L 各 离子通 道 中 每个 门 的 打 开 概率 ; / : 通过细 胞膜 的 总 电 流 密 度 ; H o d g k i n - H u x l e y 神 经 兀 模型对 生物 神 经 元 实 验记 4 0 r - 1 1 0 0 2 0 8 0 - 。 。 。 。 。 。 。 一-一 1 7 6 。 。 。 〇 。 。 ■ ^ 2 〇 [ - I > 4 0 1 | ! - 4 0 [ VWWW 2 0 \ 0 2 0 4 0 6 0 8 0 1 0 0 5 8 1 1 t [ m s ] I ( a ) ( b ) 图 2 - 5 (f) H o d g k i n - H ux l e y 神 经 元 模 型 放 电 示 意 图 ( / = l O w V ) ; ( b ) H o d gk i n- H ux l e y 神 经 元 模 型 的 / — / 曲 线 图 ( / : 神 经 元 放 电 频 率 , / : 输 入 电 流 ) 录 的 电 位变 化 进行 了 精 确 的 模拟 , 图 2 - 5 ( a ) 展示 了 刺 激 电 流 为 / = l Ow V 的 状态下 单 个 H o d g k i n - H ux l e y 神 经 元模型 的 放 电 模式 图 。 由 于 神 经 元 的 放 电 频率受 输 入 电 流 的 影 响 , 研 究 神 经 元 模 型 的 周 期 性放 电 频 率 / 作 为 输 入 电 流 / 的 函 数 通 常 是 展 示 一 个 神 经元放 电 动 力 学 的 重要特征 。 / 作 为 / 的 函 数 的 图 形 称 为 神 经 元 模型 的 频 率- 电 流 曲 线 , 或 / - / 曲 线 。 图 2 - 5 ( b ) 则 刻 画 了 H o d g k i n - Hux l e y 神 经 元 模 型 的 频 率- 电 流 ( / - / ) 曲 线 。 经典 的 H o d g k i n - H ux l e y 神 经 元 模型 建立之 后 , 从 生 物 领域跨 入到 数 学 领域 , 生 物 神 经 元 的 放 电 特性 实 现 了 用 数学模型进 行仿真 , 这对于 理 解神 经元信息 传递机制 具有 非常重要 的 指导作 用 。 尽管 H o d g k i n - H u x l e y 神 经 元模型可 以 非常精 确 的 模拟 生 物 神 经元 , 但是 由 四 个微分方程和 多 达 1 0 个变量参数组成 , 在计算性 能上有很大 的 局 限 性 , 尤 其对于 大规模神 经 元 集 群 的 动 力 学 特 性 研究 , 则 需要 超大 的 计算量和 自 由 参数估计 。 同 时 , 在数学层面 , 也很难给 出 它 的 解析解 。 于是 , 科学 家 们 为 了 降 低 H o d g k i n - H ux l e y 神 经 元 模型 的 复 杂 度 , 通过 降 低 神 经 元模 型 的 维数 , 提 出 了 许多 有 效 的 模型 , 例 如 F i t zH ug h -Na g um o 模型 、 i n t e g ra t e d - a nd - fi r e 模型 、 Mo rr i s - L e c a r 模型 、 1 7

北京郎电大学工学博士学位论文 Hindmarsh-Rose模型Is9-62]和Izhikevich神经元模型IS.63,64。本课题研究中主要使用 Hindmarsh-Rose神经元模型和Izhikevich神经元模型,接下来将分别进行简单介绍。 2.2.2 Hindmarsb-Rose神经元模型 l984年,J.L.Hindmarsh和RM.Rose根据蜗牛神经细胞实验数据,首次建立了 三维Hindmarsh-.Rose神经元模型IS刃,详细地描述了软体动物神经元放电的规律。 两年后,他们在这个三维神经元模型的基础上做了进一步的改进6例,修改后的 Hindmarsh-Rose神经元模型如下: x=y-ax+bx2-z (2-6) y=c-dx-y (2-7) 之=r[s取-xo)-司 (2-8) 这组方程中,具体参数意义可参考文献6。本研究的第三章内容,将基于HR神经 元模型对突触可塑性进行深入研究。 2.2.3 Izhikevich神经元 Izhikevich神经元模型是由Izhikevich于二十一世纪初期提出8),一经提出它就 以绝对的优势在工程计算中得到了广泛的应用,不仅可以表现出生物神经元的复杂 特性还可以提高计算效率,具体的神经元模型简化成如下的两个微分方程的形式: =02+5+10-+1 (2-9) d =albv-u) (2-10) 若v≥Vak(+30mV),则 (2-11) u←u+d. 这个模型中,参数v代表穿过神经元的细胞膜的膜电势,w表示恢复变量,神经元 外部刺激电流则用I记录,根据公式2-l11所示,当膜电位达到阙值(Vpak=30mV) 18 (C)1994-2021 China Academic Joumal Electronic Publishing House.All rights reserved.http://www.cnki.net
北 京 邮 电 大学工学博 士 学 位 论文 H i ndmar s h- Ro s e 模型 [ 5 9 _ 6 2 ] 和 I zhi k ev i c h 神经兀模型 [ 5 8 , 6 3 , 6 4 ] 。 本课题研究 中 主要使用 Hi nd mar sh- Ro s e 神 经兀模型和 I zhi ke v i c h 神经兀模型 , 接下来将分别 进行简单介绍 。 2 . 2 . 2 Hi n d ma rs h - Ro s e 神经 元模型 1 9 8 4 年, J . L . Hi ndmar s h 和 R. M. Ro s e 根据 蜗 牛神经 细 胞 实 验数据 , 首 次建立 了 三 维 Hi ndmar s h- Ro s e 神 经 兀 模 型 [ 5 7 ] , 详 细 地描 述 了 软体 动 物 神 经 兀放 电 的 规 律 。 两 年 后 , 他 们 在 这 个 三 维 神 经 元 模 型 的 基 础 上 做 了 进一 步 的 改 进 [ 6 2 ] , 修 改 后 的 Hi ndmar s h- Ro s e 神 经兀模型如 下 : x = y — ax 3 + bx1 — z ( 2 - 6 ) y = c — dx ^ — y ( 2 - 7) z = r [ 5 ( x - x〇 ) - z] ( 2 - 8 ) 这组方 程 中 , 具体参数意义可参考文献 [ 6 2 ] 。 本研究 的 第三章 内 容 , 将基于 Z/i? 神经 元模型对突触可塑性进行深入研究 。 2 . 2 . 3 Izhi kevi c h 神 经 元 I zhi kevi c h 神 经 元模型 是 由 I zhi ke v i c h 于二H ■ 世纪初 期 提 出 [ 3 8 ] , — 经 提 出 它 就 以 绝对 的 优势在工程计算 中 得 到 了 广 泛 的 应用 , 不仅可 以表现 出 生物神 经 元 的 复杂 特性还可 以提高 计算效率 , 具体 的 神经元模型简化成如下 的 两个微分方程 的 形式 : ^ = 0 . 04 v 2 + 5 v + 1 40 - ? + / ( 2 - 9) a t —  ̄ a { b v — u ) ( 2 - 1 0 ) a t 若 v 2 F_( + 3 0mV ) , 则 1 ’ ( 2 - 1 1 ) I U i H  ̄ \ d . 这个模型 中 , 参数 V 代表 穿过神 经元 的 细 胞膜 的 膜 电势 , 《 表示恢 复 变 量 , 神 经 元 外 部刺 激 电 流则 用 H己 录 , 根据公式2 - 1 1 所示 , 当 膜 电 位达到 阈 值 ( Id = 3 0mV〇 1 8