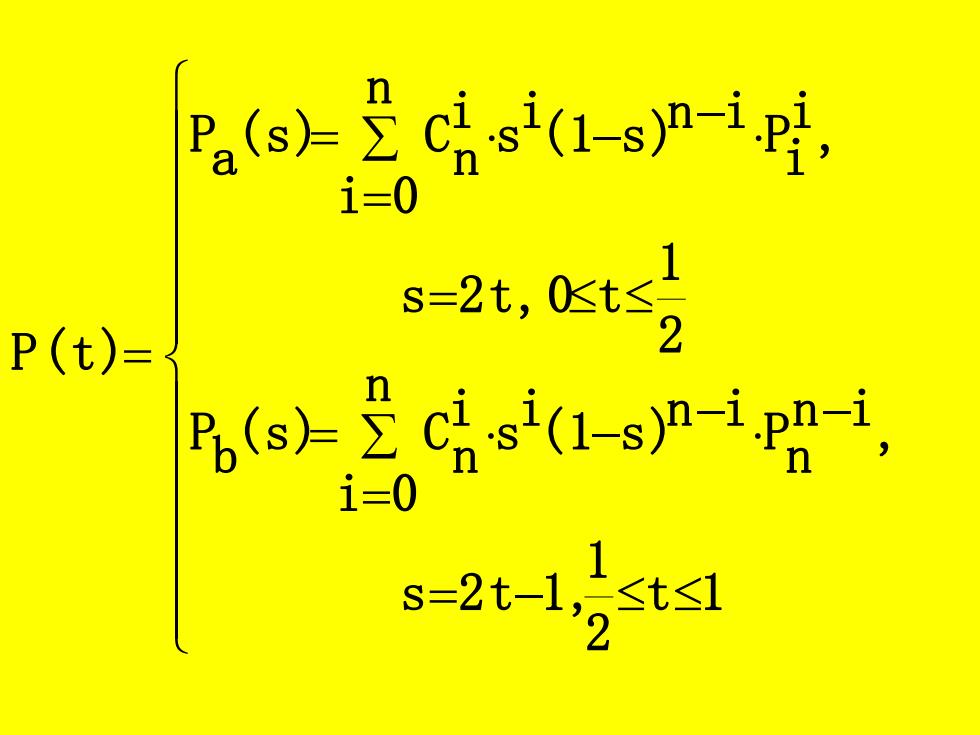
Pa(g>是cs(1-s-ip4, i=0 P(t)= s-2t,0etg Fp(s)c(1-si 1=0 s-2t-1 stal
= − = − − = − = = − = − = t 1 2 1 s 2 t 1 , , n i 0 n i n P n i ( 1 s ) i s i n (s) C b P 2 1 s 2t,0 t , n i 0 i i P n i ( 1 s ) i s i n (s) C a P P(t)

己知四点Po;P1,P23P3, 确定了一 条三次Bezierl曲线P(t),可写出下式, P(e)Bo,3e)8+B1,3e9+2,3e)2+3,3)B B0.32t)8+1,32t)月+2,32t)+,32t)写 0≤t≤ 0.32t-1)+81,32t-1)号+2,32t-1)g+,32t-1) 2Sts1
己知四点P0,P1,P2,P3,确定了一 条三次Bezier曲线P(t),可写出下式, − + − + − + − + + + = = + + + t 1 2 1 , 0 3 (2t 1)P 3,3 B 1 3 (2t 1)P 2,3 B 2 3 (2t 1)P 1,3 B 3 3 (2t 1)P 0,3 B 2 1 0 t , 3 3 (2t)P 3,3 B 2 2 (2t)P 2,3 B 1 1 (2t)P 1,3 B 0 0 (2t)P 0,3 B 3 (t)P 3,3 B 2 (t)P 2,3 B 1 (t)P 1,3 B 0 (t)P 0,3 P(t) B
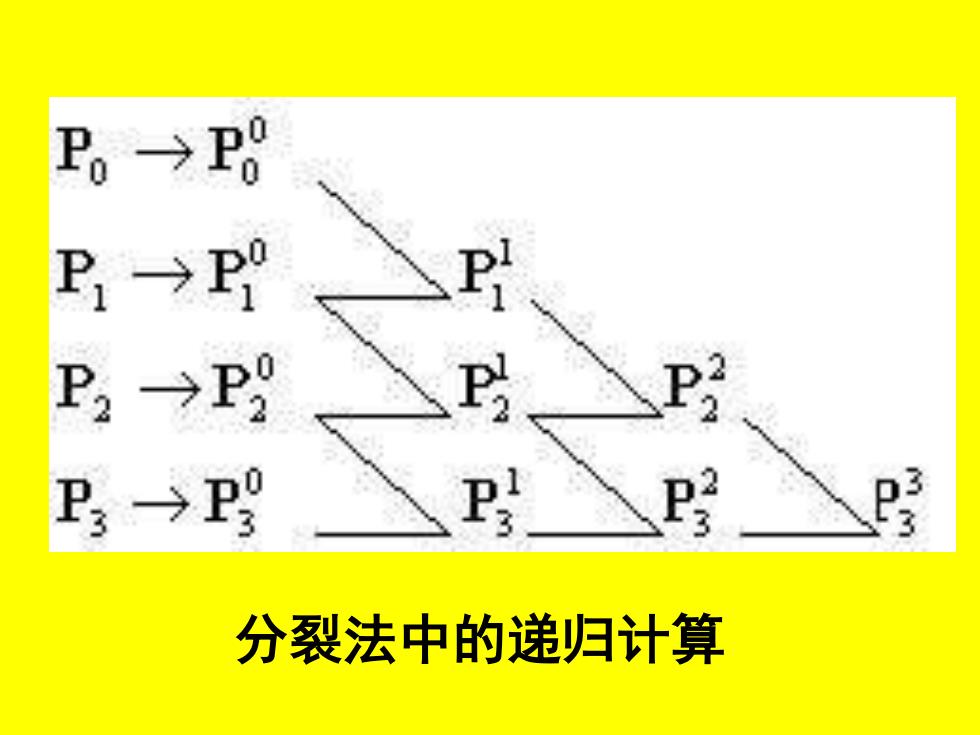
P→P8 P→ P2→P P3→9 分裂法中的递归计算
分裂法中的递归计算
P,2 P 分裂法的示意图
分裂法的示意图

可通过计算验证Bezier曲线由前 后两段构成。现以P的系数为例, 验证两端它的系数是相等的。 左端显然就是B.30)=(1-)3 先看右端。若0≤t≤§,这时就用 前半段的表达式,观察分裂计算图 注意到P中有1份Po,P中有2份, P中是份,P中是日份,因此 全部P的系数是:
可通过计算验证Bezier曲线由前 后两段构成。现以P0的系数为例, 验证两端它的系数是相等的。 左端显然就是 。 先看右端。若0≤t≤ ,这时就用 前半段的表达式,观察分裂计算图 注意到 中有1份P0, 中有 份, 中是 份, 中是 份,因此 全部P0的系数是: 3 ( ) (1 ) 0,3 B t = −t 2 0 1 P0 1 P1 2 1 2 P2 4 1 3 P3 8 1