
概率伦与散理统针」 因此得离散型随机变量关于X和Y的边缘分布函 数分别为 F,()=Fx,o)=∑2pg, x≤xj=l E,U)=Fo,)=∑Pg
( ) ( , ) , 1 = = = x x j X ij i F x F x p ( ) ( , ) . 1 = = = y y i Y ij j F y F y p 因此得离散型随机变量关于X 和Y 的边缘分布函 数分别为
概華伦与款程统外 例1已知下列分布律求其边缘分布律 0 1 16 12 49 49 12 9 49 49
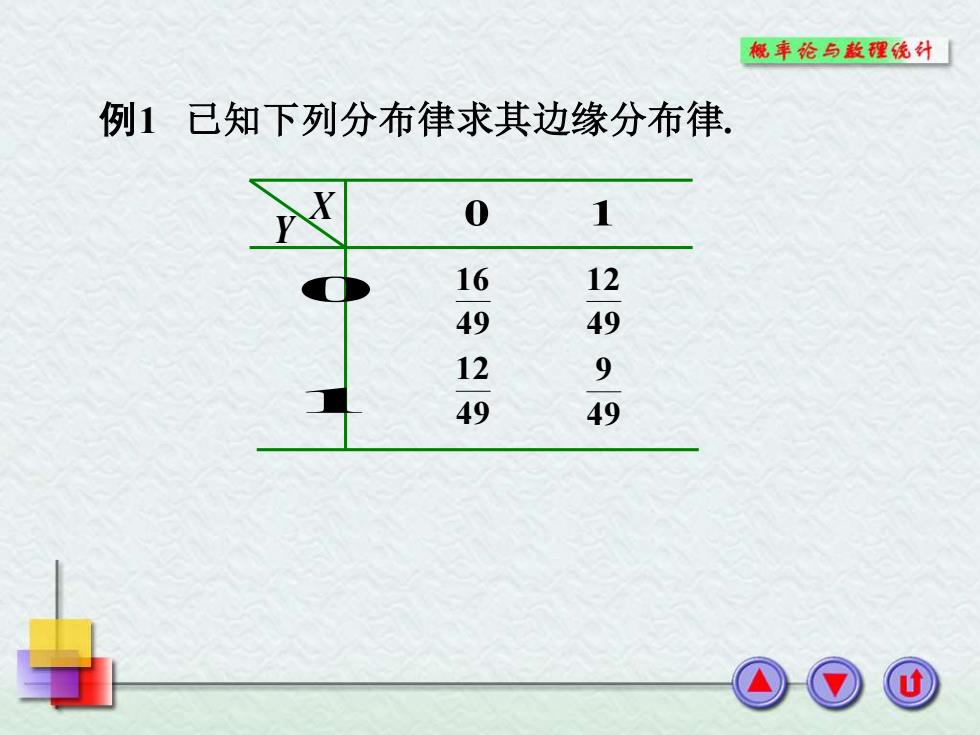
例1 已知下列分布律求其边缘分布律. X Y 0 1 49 16 49 12 49 12 49 9 1 0
棍丰伦与散程统针」 解 0 1 P.=P(Y=y} 2 12 4 + 老 73 42 + Pi.P(X=x} 4-7 13-7 注意 联合分布 二边缘分布
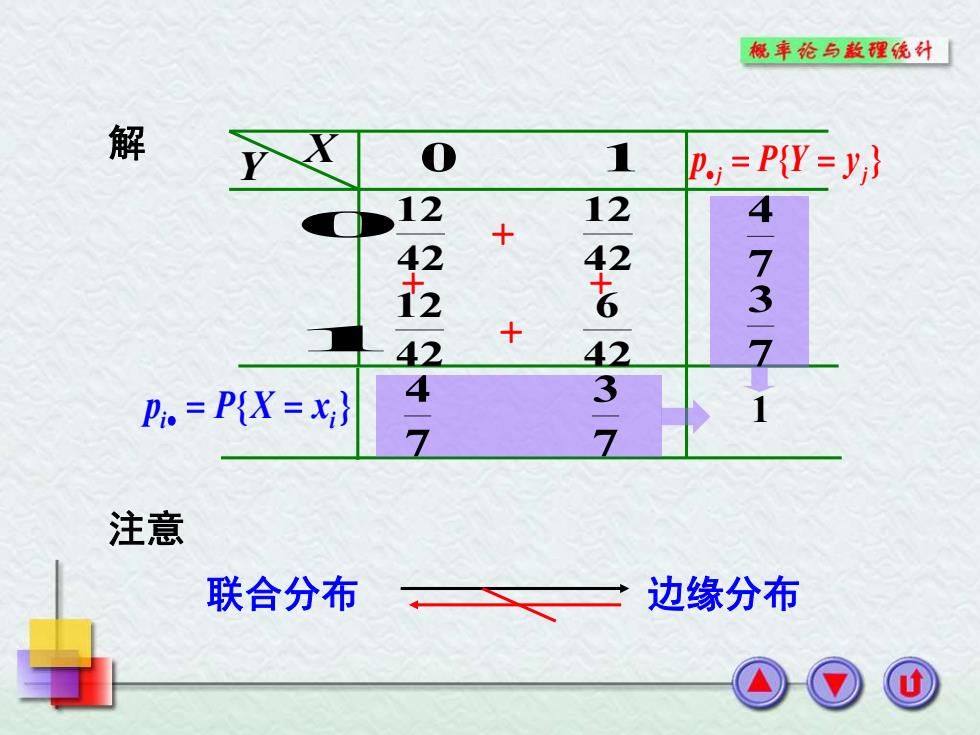
X Y 0 1 42 12 42 12 42 12 42 6 1 0 { } i i p = P X = x • { } j j p = P Y = y • 注意 联合分布 边缘分布 解 + + + + 7 4 7 3 1 7 4 7 3