
(5)至多有两个事件发生:(6)至少有两个事件发生: (7)恰有两个事件发生:(8)恰有一个事件发生. 分析:利用事件的运算关系及性质来描述事件 解:(1)ABC:(2)ABC:(3)ABC或AUBOC:(4)AUBUC 或ABCABCABCUABCABCUABCABC:(5)AUBUC或 ABCABCUABCUABCUABCUABCUABC: (6)ABUACBC ABCUABCABCUABC (7)ABCUABCUABC:(8)ABCABCUABC. 【例3】把n个不同的球随机地放入N(N≥)个盒子中,求下列事件的概率: (1)某指定的n个盒子中各有一个球: (2)任意n个盒子中各有一个球: (3)指定的某个盒子中恰有m(m<n)个球 分析:这是古典概率的一个典型问题,许多古典概率的计算问题都可归结为 这一类型.每个球都有N种放法,n个球共有N"种不同的放法.“某指定的n个 盒子中各有一个球”相当于n个球在n个盒子中的全排列:与(1)相比,(2) 相当于先在N个盒子中选n个盒子,再放球:(3)相当于先从n个球中取m个 放入某指定的盒中,再把剩下的n一m个球放入N-1个盒中. 解:样本空间中所含的样本点数为N”. )该事件所含的样本点数是川,故:p=以:
5 (5)至多有两个事件发生; (6)至少有两个事件发生; (7)恰有两个事件发生; (8)恰有一个事件发生. 分析:利用事件的运算关系及性质来描述事件. 解:(1) ABC ;(2) ABC ;(3) ABC 或 ABC ;(4) ABC 或 ABC ABC ABC ABC ABC ABC ABC ;(5) ABC 或 ABC ABC ABC ABC ABC ABC ABC ; (6) ABACBC 或 ABC ABC ABC ABC ; (7) ABC ABC ABC ;(8) ABC ABC ABC . 【例 3】把 n 个不同的球随机地放入 N(N n) 个盒子中,求下列事件的概率: (1)某指定的 n 个盒子中各有一个球; (2)任意 n 个盒子中各有一个球; (3)指定的某个盒子中恰有 m(m n) 个球. 分析:这是古典概率的一个典型问题,许多古典概率的计算问题都可归结为 这一类型.每个球都有 N 种放法, n 个球共有 n N 种不同的放法.“某指定的 n 个 盒子中各有一个球”相当于 n 个球在 n 个盒子中的全排列;与(1)相比,(2) 相当于先在 N 个盒子中选 n 个盒子,再放球;(3)相当于先从 n 个球中取 m 个 放入某指定的盒中,再把剩下的 n−m 个球放入 N −1 个盒中. 解:样本空间中所含的样本点数为 n N . (1)该事件所含的样本点数是 n! ,故: n N n p = ! ;

(2)在N个盒子中选n个盒子有C。种选法,故所求事件的概率为: p=C (3)从n个球中取m个有Cm种选法,剩下的n-m个球中的每一个球都有 N-l种放法,故所求事件的概率为:p=C.W-1人 N 【例4】随机地向由0<y<1州<所围成的正方形内璃一点,点落在该正方形 内任何区域的概率与区域面积成正比,求原点和该点的连线与x轴正向的夹角小 于红的版率 分析:这是一个几何概率问题,通常可借助几何上的度量(长度、面积、体 积或容积等)来合理地规定其概率. 解:用S表示该正方形的面积,S表示 图1.2阴影部分面积,则所求的概率为: 0 图1.2 【例5】设事件A与B互不相容,且P(A)=p,P(B)=q,求下列事件的概率: P(AB),P(AUB),P(AB),P(AB). 分析:按概率的性质进行计算. 解:A与B互不相容,所以AB=中,P(AB)=P()=0:
6 (2)在 N 个盒子中选 n 个盒子有 n CN 种选法,故所求事件的概率为: n n N N C n p ! = ; (3)从 n 个球中取 m 个有 m Cn 种选法,剩下的 n−m 个球中的每一个球都有 N −1 种放法,故所求事件的概率为: n n m n N N N p C − − = ( 1) . 【例 4】随机地向由 2 1 0 y 1、x 所围成的正方形内掷一点,点落在该正方形 内任何区域的概率与区域面积成正比,求原点和该点的连线与 x 轴正向的夹角小 于 4 3 的概率. 分析:这是一个几何概率问题,通常可借助几何上的度量(长度、面积、体 积或容积等)来合理地规定其概率. 解:用 S 表示该正方形的面积, 1 S 表示 图 1.2 阴影部分 面积,则所求的概率为: 8 7 1 ) 2 1 ( 2 1 1 2 1 = − = = S S p . 【例 5】设事件 A 与 B 互不相容,且 P(A) = p, P(B) = q ,求下列事件的概率: P(AB), P(A B), P(AB), P(AB) . 分析:按概率的性质进行计算. 解: A 与 B 互不相容,所以 AB = , P(AB) = P() = 0 ; x y 1 2 1 2 1 − 0 图 1.2

P(A+B)=P()+P(B)=p+q:由于A与B互不相容,这时AB=A,从而 P(AB)=P()=P:由于AB=AUB,从而 P(AB)=P(AUB)=1-P(AUB)=1-(p+q). 【例6】某住宅楼共有三个孩子,己知其中至少有一个是女孩,求至少有一个是 男孩的概率(假设一个小孩为男或为女是等可能的). 分析:在已知“至少有一个是女孩”的条件下求“至少有一个是男孩”的概 率,所以是条件概率间题根据公式P(B1A)=PL4,必须求出P(AB,P氏A). P(4) 解:设A={至少有一个女孩},B={至少有一个男孩},则A={三个全是男孩} B={仁个全是女孩},于是 11 PA)=2宁-8PB,事件AB为“至少有一个女孩且至少有一个男孩”,因 为AB=AUB,且AB=D,所以P(AB)=1-P(AB)=1-P(AUB)= 1-团+P=1--P=1-闭-从面:在起砂有 3 一个为女孩的条件下,求至少有一个是男孩的概率为: 3 【例7】某电子设备制造厂所用的品体管是由三家元件制造厂提供的.根据以往的 记录有以下的数据(表1-1)
7 P(A+ B) = P(A) + P(B) = p + q ;由于 A 与 B 互不相容,这时 AB = A ,从而 P(AB) = P(A) = p ;由于 AB = A B ,从而 P(AB) = P(A B) =1− P(A B) =1− ( p + q) . 【例 6】某住宅楼共有三个孩子,已知其中至少有一个是女孩,求至少有一个是 男孩的概率(假设一个小孩为男或为女是等可能的). 分析:在已知“至少有一个是女孩”的条件下求“至少有一个是男孩”的概 率,所以是条件概率问题.根据公式 ( ) ( ) ( | ) P A P AB P B A = ,必须求出 P(AB), P(A) . 解:设 A ={至少有一个女孩},B ={至少有一个男孩},则 A ={三个全是男孩}, B ={三个全是女孩},于是 ( ) 8 1 2 1 ( ) 3 P A = = = P B ,事件 AB 为“至少有一个女孩且至少有一个男孩”,因 为 AB = A B ,且 AB = ,所以 P(AB) =1− P(AB) =1− P(A B) = 8 7 , ( ) 1 ( ) 4 3 ) 8 1 8 1 1−[P(A) + P(B)] =1− ( + = P A = − P A = ,从而,在已知至少有 一个为女孩的条件下,求至少有一个是男孩的概率为: 7 6 8 7 4 3 ( ) ( ) ( | ) = = = P A P AB P B A . 【例 7】某电子设备制造厂所用的晶体管是由三家元件制造厂提供的.根据以往的 记录有以下的数据(表 1-1)
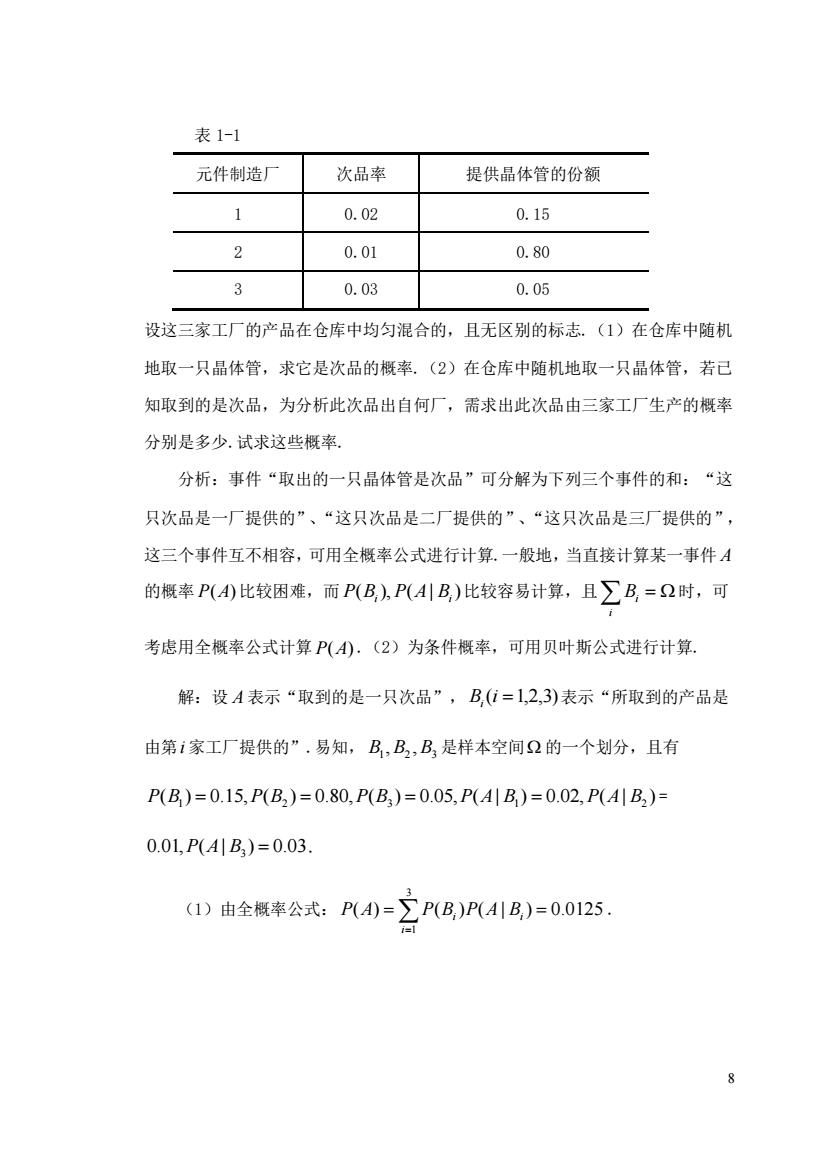
表1-1 元件制造厂 次品率 提供品体管的份额 1 0.02 0.15 2 0.01 0.80 0.03 0.05 设这三家工厂的产品在仓库中均匀混合的,且无区别的标志.(1)在仓库中随机 地取一只品体管,求它是次品的概率.(2)在仓库中随机地取一只品体管,若已 知取到的是次品,为分析此次品出自何厂,需求出此次品由三家工厂生产的概率 分别是多少.试求这些概率 分析:事件“取出的一只晶体管是次品”可分解为下列三个事件的和:“这 只次品是一厂提供的”、“这只次品是二厂提供的”、“这只次品是三厂提供的”, 这三个事件互不相容,可用全概率公式进行计算.一般地,当直接计算某一事件A 的概率P(4)比较困难,而P(B,)P(AB)比较容易计算,且∑B,=2时,可 考虑用全概率公式计算P(A).(2)为条件概率,可用贝叶斯公式进行计算 解:设A表示“取到的是一只次品”,B,(i=1,2,3)表示“所取到的产品是 由第1家工厂提供的”.易知,B,B2,B是样本空间2的一个划分,且有 P(B)=0.15,P(B,)=0.80,P(B,)=0.05,P(A|B)=0.02,P(A|B)= 0.0L,P(AB)=0.03. (I)由全概率公式:P4)=∑P(B,)PAB)=0.0125 8
8 表 1-1 元件制造厂 次品率 提供晶体管的份额 1 0.02 0.15 2 0.01 0.80 3 0.03 0.05 设这三家工厂的产品在仓库中均匀混合的,且无区别的标志.(1)在仓库中随机 地取一只晶体管,求它是次品的概率.(2)在仓库中随机地取一只晶体管,若已 知取到的是次品,为分析此次品出自何厂,需求出此次品由三家工厂生产的概率 分别是多少.试求这些概率. 分析:事件“取出的一只晶体管是次品”可分解为下列三个事件的和:“这 只次品是一厂提供的”、“这只次品是二厂提供的”、“这只次品是三厂提供的”, 这三个事件互不相容,可用全概率公式进行计算.一般地,当直接计算某一事件 A 的概率 P(A) 比较困难,而 ( ), ( | ) P Bi P A Bi 比较容易计算,且 = i Bi 时,可 考虑用全概率公式计算 P(A) .(2)为条件概率,可用贝叶斯公式进行计算. 解:设 A 表示“取到的是一只次品”, B (i =1,2,3) i 表示“所取到的产品是 由第 i 家工厂提供的”.易知, 1 2 3 B ,B ,B 是样本空间 的一个划分,且有 ( ) 0.15, ( ) 0.80, ( ) 0.05, ( | ) 0.02, ( | ) P B1 = P B2 = P B3 = P A B1 = P A B2 = 0.01,P(A| B3 ) = 0.03. (1)由全概率公式: ( ) ( ) ( | ) 0.0125 3 1 = = i= P A P Bi P A Bi

(2)由贝叶斯公式: P代B10=P1IB)B2=024,PA,1A0=064,PB1)=012.以上结 P(A) 果表明,这只次品来自第二家工厂的可能性最大 【例8】一名工人照看A、B、C三台机床,已知在1小时内三台机床各自不需 要工人照看的概率为P(A)=0.9,P(B)=0.8,P(C)=0.7.求1小时内三台机床至 多有一台需要照看的概率. 分析:每台机床是否需要照看是相互独立的,这样,可根据事件的独立性性 质及加法公式进行计算 解:各台机床需要照看的事件是相互独立的,而三台机床至多有一台需要照 看的事件D可写成:D=ABC+ABC+ABC+ABC,则由加法公式与独立性 性质得:P(D)=P(ABC+ABC+ABC+ABC)=P(ABC)H P(ABC)+P(ABC)+P(ABC)=P(A)P(B)P(C)+P(A)P(B)P(C)+ P(A)P(B)P(C)+P(A)P(B)P(C)=0.902. 【例9】某车间有10台同类型的设备,每台设备的电动机功率为10千瓦.己知每 台设备每小时实际开动12分钟,它们的使用是相互独立的.因某种原因,这天供 电部门只能给车间提供50千瓦的电力.问该天这10台设备能正常运作的概率是多 少? 分析:由题意知,所要求的概率就是求“该天同时开动的设备不超过5台” 这一事件的概率.因为每台设备的使用是相互独立的,且在某一时刻,设备只有开
9 (2)由贝叶斯公式: 0.24, ( | ) 0.64, ( | ) 0.12 ( ) ( | ) ( ) ( | ) 2 3 1 1 1 = = P B A = P B A = P A P A B P B P B A .以上结 果表明,这只次品来自第二家工厂的可能性最大. 【例 8】一名工人照看 A、B、C 三台机床,已知在 1 小时内三台机床各自不需 要工人照看的概率为 P(A) = 0.9, P(B) = 0.8, P(C) = 0.7 .求1小时内三台机床至 多有一台需要照看的概率. 分析:每台机床是否需要照看是相互独立的,这样,可根据事件的独立性性 质及加法公式进行计算. 解:各台机床需要照看的事件是相互独立的,而三台机床至多有一台需要照 看的事件 D 可写成: D = ABC + ABC + ABC + ABC ,则由加法公式与独立性 性质得: P(D) = P(ABC + ABC + ABC + ABC) = P(ABC) + P(ABC) + P(ABC) + P(ABC) = P(A)P(B)P(C) + P(A)P(B)P(C) + P(A)P(B)P(C) + P(A)P(B)P(C) =0.902. 【例 9】某车间有 10 台同类型的设备,每台设备的电动机功率为 10 千瓦.已知每 台设备每小时实际开动 12 分钟,它们的使用是相互独立的.因某种原因,这天供 电部门只能给车间提供50千瓦的电力.问该天这10台设备能正常运作的概率是多 少? 分析:由题意知,所要求的概率就是求“该天同时开动的设备不超过 5 台” 这一事件的概率.因为每台设备的使用是相互独立的,且在某一时刻,设备只有开