
回顾 方程求根:给定f,求x使得f(x)=0 -连续函数:二分法 - 1-Lipschitz:转换为不动点迭代方程后使用不动点迭代法 -根的敏感性 这节课: 一可导且导涵数也已知:牛顿法,二次收敛 -插值(Interpolation):给定一些不完整的观察值,想要推理出全景 图像 0.12 0.10 0.08 0.06 0.04 0.02 0 20 3040 4
回顾 • 方程求根:给定�,求�使得�(�) = 0 – 连续函数:二分法 – 1-Lipschitz: 转换为不动点迭代方程后使用不动点迭代法 – 根的敏感性 • 这节课: – 可导且导函数也已知:牛顿法,二次收敛 – 插值(Interpolation):给定一些不完整的观察值,想要推理出全景 图像 4
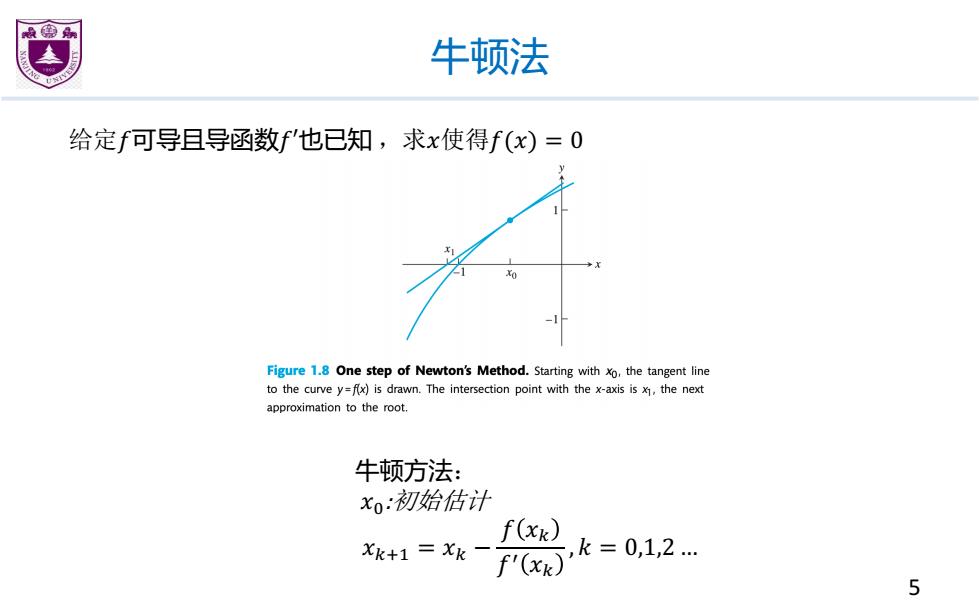
牛顿法 给定f可导且导函数f'也已知,求x使得f(x)=0 Figure 1.8 One step of Newton's Method.Starting with xo.the tangent line to the curve y=fx)is drawn.The intersection point with the x-axis is x,the next approximation to the root. 牛顿方法: xo:初始估计 f(xk) Xk+1=Xk- ,k=0,1,2. f'(xk 5
牛顿法 5 给定�可导且导函数�′也已知 ,求�使得�(�) = 0 牛顿方法: �!:初始估计 �"#$ = �" − � �" �% �" , � = 0,1,2 …

牛顿法的二次收敛(Quadratic convergence) 记e:=lx:一r为i次迭代的误差 局部收敛:在某个足够小的邻域里面,任意的初始值都 会收敛 二次收敛:如果M=即号<0,月 称该迭代方法二 次收敛。 定理.如果f二次可导且f'(r)≠0,其中r满足f(r)=0,那 么牛顿法在局部二次收敛到r,且 ei+1 e子 6
牛顿法的二次收敛 (Quadratic convergence) 记�/ = �/ − � 为i次迭代的误差 • 局部收敛:在某个足够小的邻域里面,任意的初始值都 会收敛 • 二次收敛:如果� = lim /→1 2!"# 2! $ < ∞,则称该迭代方法二 次收敛。 定理. 如果�二次可导且�! � ≠ 0,其中�满足� � = 0,那 么牛顿法在局部二次收敛到�,且 lim /→1 �/34 �/ 5 = �66 � 2�6 � 6

牛顿法的二次收敛分析:不动点方程 定理.如果f二次连续可导且f'(r)≠0,其中r满足fr)=0,那么 牛顿法在扃部二次收敛到,且 lim +1= f"(r) i-→00 e 2f'(r) 证明:首先注意到牛顿法等价于以下不动点方程xk+1=g(x), 其中g(x)=x- ·g的不动点对应于f的根。 f(x) g'(x)=1- f'(x)2-f(x)f"(x)f(x)f"(x) f'(x)2 f'(x)2 在g的不动点处,有g(r)=0.因此牛顿法是局部收敛的
牛顿法的二次收敛分析:不动点方程 定理. 如果�二次连续可导且�! � ≠ 0,其中�满足� � = 0,那么 牛顿法在局部二次收敛到�,且 lim /→1 �/34 �/ 5 = �66 � 2�6 � 证明:首先注意到牛顿法等价于以下不动点方程�734 = �(�7), 其中� � = � − 8 9 8% 9 . �的不动点对应于�的根。 �6 � = 1 − �6 � 5 − � � �66 � �6 � 5 = � � �66 � �6 � 5 . 在�的不动点处, 有�6 � = 0. 因此牛顿法是局部收敛的。 7

牛顿法的二次收敛分析 定理.如果f二次可导且f'()≠0,其中r满足f)=0,那么牛顿法在局部二次收敛到r,且 lim ei+1 f"(r) e 2f'r) 证明:考虑第i次迭代,在r处进行Taylor展开有: fr))(").for some5 2 因为r满足f(r)=0,化简得到 f(xi) Xi- -=-xf") f'(x) 2 f'(xi) 回顾牛顿法的迭代方程: eit1 1xit1 -rl e2 f"() 2f'(x) 由局部收敛可知,只要足够的接近r,则有x→r且→r。由f”和f'的连续性可知 f"(ξ) f"(r) lim ei+1 i→00 S3 lim 2f'(x:) 2f'(r) 8
牛顿法的二次收敛分析 定理. 如果�二次可导且�! � ≠ 0,其中�满足� � = 0,那么牛顿法在局部二次收敛到�,且 lim !→# �!$% �! & = �'' � 2�' � 证明:考虑第�次迭代,在�处进行Taylor展开有: � � = � �! + � − �! �' �! + � − �! & 2 �'' �! , for some �! 因为�满足� � = 0,化简得到 �! − � �! �' �! − � = � − �! & 2 �'' �! �' �! 回顾牛顿法的迭代方程: �!$% = |�!$% − �| = �! & �'' �! 2�' �! 由局部收敛可知,只要足够的接近�, 则有�! → �且�! → �。由�''和�' 的连续性可知 lim !→# �!$% �! & = lim !→# �'' �! 2�' �! = �'' � 2�' � 8