
8关于二端口的对称性 满足互易性质的二端口, 只有3个参数是独立的。 U, 若二端口的Y参数不仅 1'O 52 有Y2=Y2,而且还有 YY2,则这样的二端 对上图的Π型电路, 口在电气上是对称的, 当Y。=Y时,就变成 称为对称二端口,它只 对称二端口。 有2个参数是独立的。 不仅如此,它在结 把对称二端口的两个端 构上也是对称的。 口互换位置后与外电路 注意:电气上对称 连接,外部特性不会有 的二端口在结构上 任何变化。 不一定对称。 11
11 关于二端口的对称性 1 1' 2 2' Ya Yb Yc . I2 + - . U1 . I1 + - . U2 满足互易性质的二端口, 只有3个参数是独立的。 若二端口的Y参数不仅 有Y12 = Y21,而且还有 Y11=Y22,则这样的二端 口在电气上是对称的, 称为对称二端口,它只 有2个参数是独立的。 把对称二端口的两个端 口互换位置后与外电路 连接,外部特性不会有 任何变化。 对上图的P型电路, 当Ya =Yc时,就变成 对称二端口。 不仅如此,它在结 构上也是对称的。 注意:电气上对称 的二端口在结构上 不一定对称

二、Z(阻抗)参数方程及Z参数 1.Z参数方程可以仿照Y参数 用叠加原理得到。 U U, >Y参数方程与Z参数方程之间 有对偶关系:Y一Z 2.各参数的含义 i一U短路一开路 U=Z11+Z122 U2=Z21i1+Z22i 为口2开路,口1的输入阻抗。 02 Uz Z21= Z12= U i2-0 ii=0 1i=0 为口2(口1)开路,2与1(1与2) 为口1-1开路时,口 之间的开路转移阻抗。 2-2'的输入阻抗。 12
12 二、Z(阻抗)参数方程及Z参数 1. Z参数方程 可以仿照Y参数 用叠加原理得到。 ➢ Y参数方程与Z参数方程之间 有对偶关系: . I1 . I2 + - . U1 + - . U2 Y Z . I . U 短路 开路 . U1 = Z11 . I1 + Z12 . I2 . U2 = Z21 . I1 + Z22 . I2 Z11 = . U1 . I1 . I2=0 Z21 = . U2 . I1 . I2=0 Z12 = . U1 . I2 . I1=0 Z22 = . U2 . I2 . I1=0 为口2开路,口1的输入阻抗。 为口1-1'开路时,口 2-2'的输入阻抗。 为口2(口1)开路,2与1(1与2) 之间的开路转移阻抗。 2. 各参数的含义

把Z参数方程写成矩阵形式: 比较可知: 图-斗 开路阻抗矩阵Z与短路 导纳矩阵Y存在互为逆 阵的关系: 可得Z(阻抗)参数矩阵 Z=Y-1或Y=Zl def ZaZ 对具有互易性质的二端 口,总有Z2=Z12 Ay=Y1Y22-Y12Y21 3.与Y参数的关系 网 [U, 4.Z参数的求法开路法 实验测量或分析电路。 13
13 把Z参数方程写成矩阵形式: 可得Z(阻抗)参数矩阵 • 对具有互易性质的二端 口,总有Z21=Z12。 3. 与Y 参数的关系 . U1 . U2 = Z11 Z12 Z21 Z22 . I1 . I2 = Z . I1 . I2 Z def Z11 Z12 Z21 Z22 . I1 . I2 = Y11 Y12 Y21 Y22 . U1 . U2 = Y . U1 . U2 比较可知: 开路阻抗矩阵Z与短路 导纳矩阵Y存在互为逆 阵的关系: Z = Y -1 或 Y = Z -1 Z11 Z12 Z21 Z22 = DY 1 Y22 -Y12 -Y21 Y11 DY= Y11 Y22 - Y12Y21 4. Z参数的求法 开路法 实验测量或分析电路

举例:求P438习题16-2图(a)的Z参数矩阵。 12 解:为对称二端口, 只有两个独立参数。 12 根据参数的含义: 123 Z1=Z2= (1+1)×1 (1+1)+1 按定义求Z21: 43 Z= 要获得 =}i+i=号1 Y参数 号n Z2-Z12 -Z21 △zZ11Z22-Z12Z21 14
14 举例:求P438习题16-2图(a) 的Z参数矩阵。 解:为对称二端口, 只有两个独立参数。 根据参数的含义: 按定义求 Z21 : 1W 1W 1W 1W 1 1' 2 2' Z11 = Z22 = (1+1)+1 (1+1)×1 +1 W 1W 1W 1W 1W 1 1' 2 2' 1 3 1 I + - + - . U1 . U2 . I . 2=0 I1 . I1 . + I1 = . U2 = Z21 = . U2 . I1 . I2=0 Z = W Y11 Y12 Y21 Y22 = DZ 1 Z22 -Z12 -Z21 Z11 DZ= Z11 Z22 - Z12Z21 要获得 Y 参数 = 3 5 3 1 . I1 3 4 . I1 = W 3 4 Z12 = Z21 = W 3 4 3 5 3 4 3 4 3 5
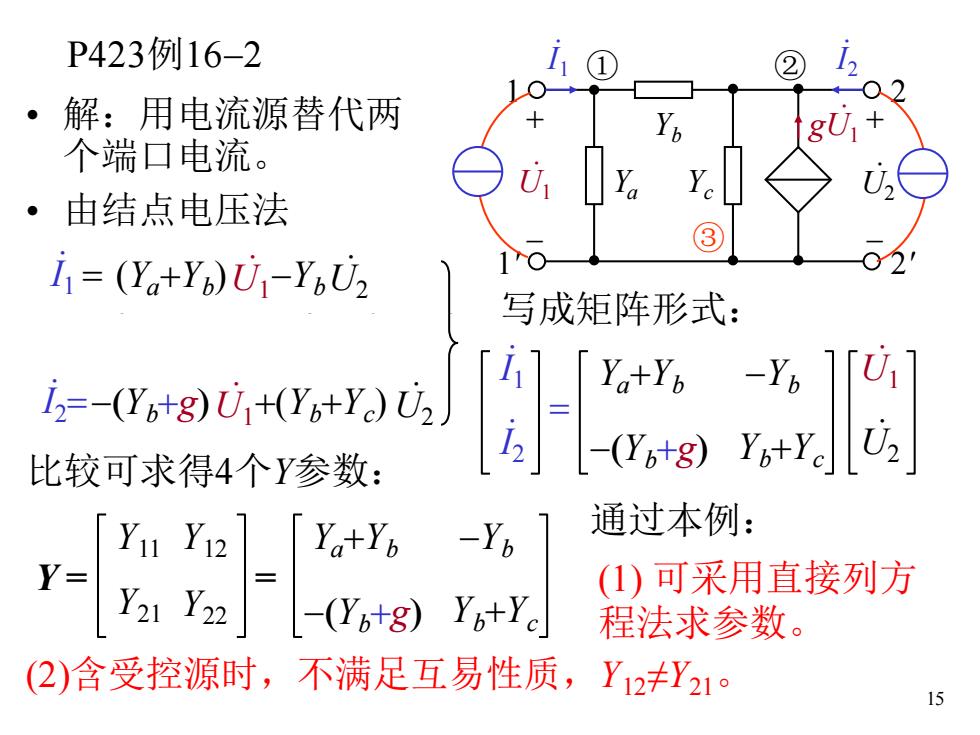
P423例16-2 ·解:用电流源替代两 个端口电流。 ·由结点电压法 ③ I=(Ya+Yb)U-YbU2 写成矩阵形式: 比较可求得4个Y参数: -Y6 通过本例: (1)可采用直接列方 YptYe 程法求参数。 (2)含受控源时,不满足互易性质,Y12≠Y21 15
15 P423例16-2 • 解:用电流源替代两 个端口电流。 • 由结点电压法 Ya Yc Yb + - + - . gU1 . U1 . U2 . I1 . I2 1 1' 2 2' ① ② ③ (Ya+Yb ) . U1 -Yb . U2 . I1 = -Yb . U1 + (Yb+Yc ) . U2 = . I2+ . gU1 . I2=-(Yb+g) . U1 +(Yb+Yc ) . U2 写成矩阵形式: . I1 . I2 = Ya+Yb -Yb -(Yb+g) Yb+Yc . U1 . U2 比较可求得4个Y参数: Y = Y11 Y21 Y12 Y22 = Ya+Yb -Yb -(Yb+g) Yb+Yc 通过本例: (1) 可采用直接列方 程法求参数。 (2)含受控源时,不满足互易性质,Y12≠Y21