
y=f(x) △f=fa+dx)-fa) △L=f'(a)dx (a,f(a)) dx When dx is a small change in x, Tangent the corresponding change in line the linearization is precisely df. →X 0 e a +dx
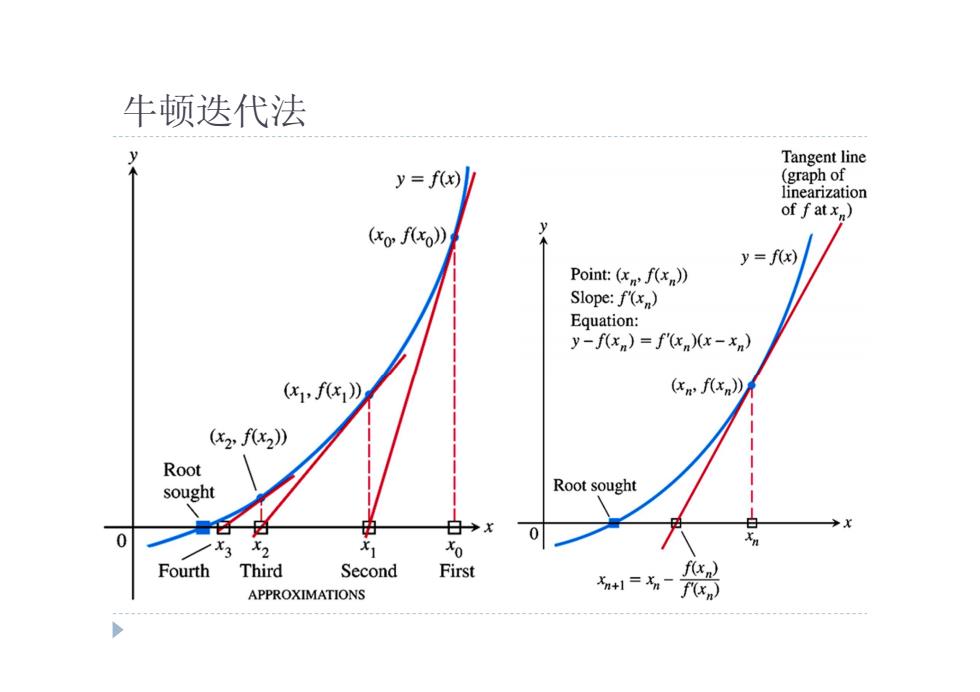
牛顿迭代法 Tangent line y=f(x)l (graph of linearization of f atxn) (xo f(xo)》 y=f(x) Point:(cn,fxn》 Slope:f(x) Equation: y-f(xn)=f(xn)(x-x) ,f) (xn f(xn)》 (2f0x2》 Root sought Root sought 日→x 0 3 0 0 Fourth Third Second First f(xn) APPROXIMATIONS ntl=n-f(xn
牛顿迭代法