
例2.6,2,以绝对收入假设为理论假设、以截面 数据为样本建立居民消费函数: C=Bo+BYi+14 将居民按照收入等距离分成组,取组平均数为样 本观测值。 一般情况下,居民收入服从正态分布:中等收入 组人数多,两端收入组人数少。而人数多的组平均 数的误差小,人数少的组平均数的误差大。 所以样本观测值的观测误差随着解释变量观测值 的不同而不同,往往引起异方差性
例2.6,2,以绝对收入假设为理论假设、以截面 数据为样本建立居民消费函数: Ci=0+1Yi+I 将居民按照收入等距离分成n组,取组平均数为样 本观测值。 一般情况下,居民收入服从正态分布:中等收入 组人数多,两端收入组人数少。而人数多的组平均 数的误差小,人数少的组平均数的误差大。 所以样本观测值的观测误差随着解释变量观测值 的不同而不同,往往引起异方差性

例2.6.3,以某一行业的企业为样本建立企业生产 函数模型 Yi=ABI KB2 LB3eui 被解释变量:产出量Y 解释变量:资本K、劳动L、技术A, 那么:每个企业所处的外部环境对产出量的影响被 包含在随机误差项中。 每个企业所处的外部环境对产出量的影响程度不 同,造成了随机误差项的异方差性。 这时,随机误差项的方差并不随某一个解释变量 观测值的变化而呈规律性变化,呈现复杂型
例2.6.3,以某一行业的企业为样本建立企业生产 函数模型 Yi=Ai 1 Ki 2 Li 3e i 被解释变量:产出量Y 解释变量:资本K、劳动L、技术A, 那么:每个企业所处的外部环境对产出量的影响被 包含在随机误差项中。 每个企业所处的外部环境对产出量的影响程度不 同,造成了随机误差项的异方差性。 这时,随机误差项的方差并不随某一个解释变量 观测值的变化而呈规律性变化,呈现复杂型

四、异方差的类型 同方差性假定:σ2=常数≠f仪) 异方差时: o2=f(Xi) 异方差一般可归结为三种类型: (1)单调递增型:ō随X的增大而增大 (2)单调递减型:σ随X的增大而减小 (3)复杂型:ō2与X的变化呈复杂形式
四、异方差的类型 同方差性假定:i 2 = 常数 f(Xi ) 异方差时: i 2 = f(Xi ) 异方差一般可归结为三种类型: (1)单调递增型: i 2随X的增大而增大 (2)单调递减型: i 2随X的增大而减小 (3)复 杂 型: i 2与X的变化呈复杂形式
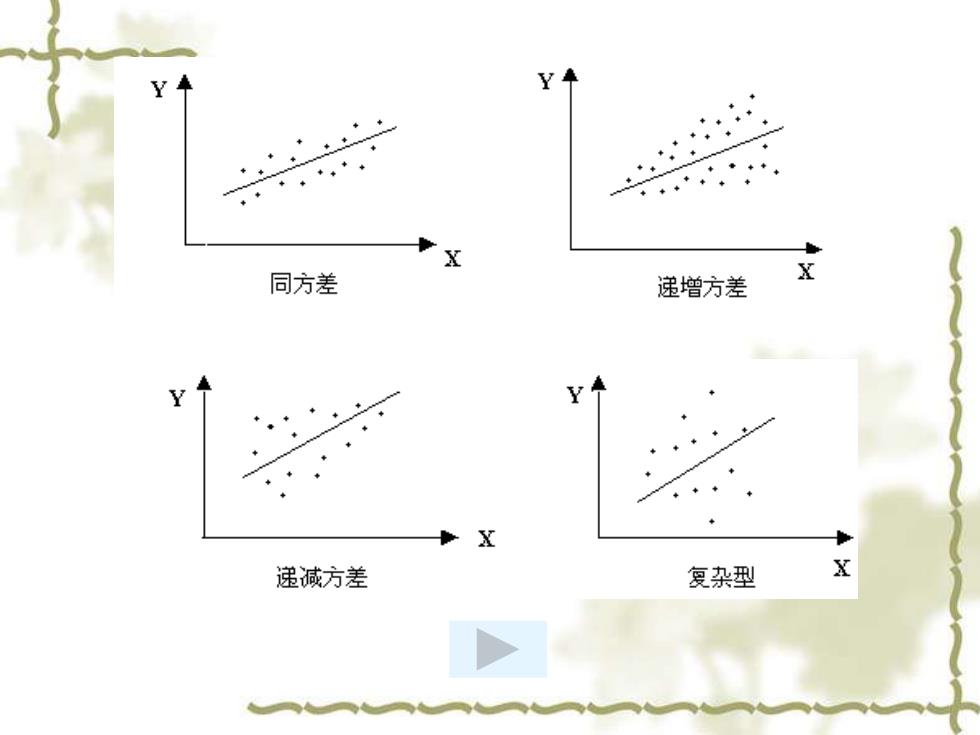
同方差 递增方差 递减方差 复杂型

四、异方差性的后果 计量经济学模型一旦出现异方差性,如果仍采 用OLS估计模型参数,会产生下列不良后果: 1、参数估计量非有效 OLS估计量仍然具有无偏性,但不具有有效性 因为在有效性证明中利用了 E(μμ')=o2I 而且,在大样本情况下,尽管参数估计量具有 一致性,但仍然不具有渐近有效性
四、异方差性的后果 计量经济学模型一旦出现异方差性,如果仍采 用OLS估计模型参数,会产生下列不良后果: 1、参数估计量非有效 OLS估计量仍然具有无偏性,但不具有有效性 因为在有效性证明中利用了 E(’)=2 I 而且,在大样本情况下,尽管参数估计量具有 一致性,但仍然不具有渐近有效性