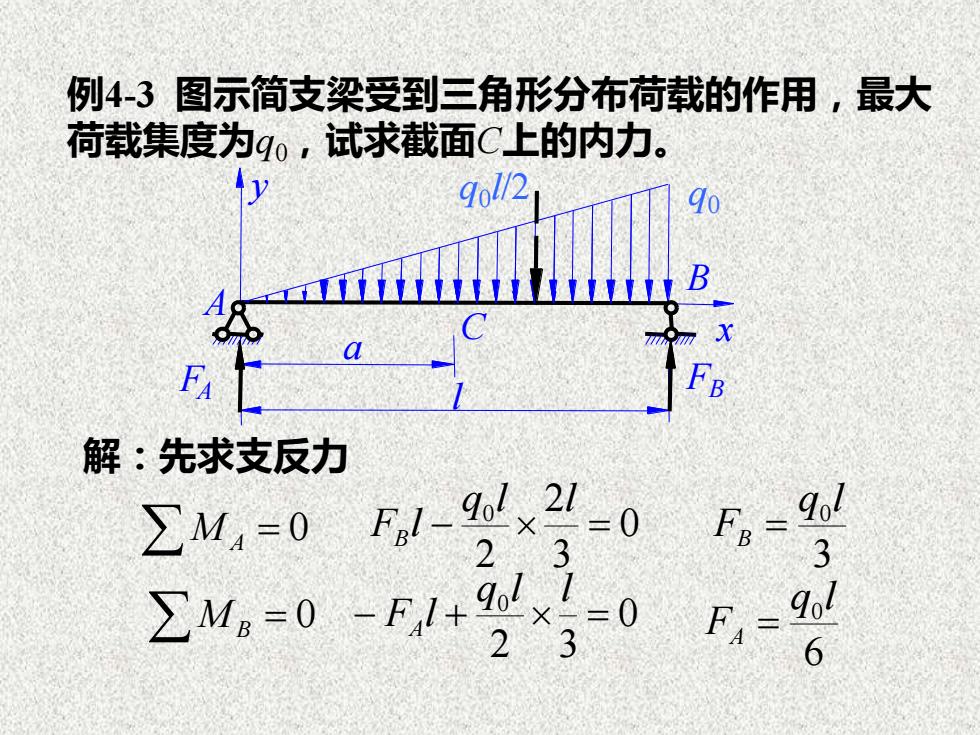
例4-3图示简支梁受到三角形分布荷载的作用,最大荷载集度为g。,试求截面C上的内力ty9ol/2qoB-C17aFBFA解:先求支反力9o/ 219olFsl=0FBZM.=0X37329ol9ol-F,I+ZM=0二=0F =X236
例4-3 图示简支梁受到三角形分布荷载的作用,最大 荷载集度为q0,试求截面C上的内力。 解:先求支反力 M A = 0 M B = 0 0 3 2 2 0 − = q l l F l B 0 2 3 0 − + = q l l F l A 3 0 q l FB = 6 0 q l FA = x y A B a l C q0 FA FB q0 l/2

截面C的内力a/3Mqorq(x) =福1aFscTA9012a-29la=FFsc+A1621la3ayqolJoaaMc= F xa+O+213661思考:是否可以将梁上的分布荷载全部用静力等效后的合力代替来求截面C的内力?
截面C的内力 l q l q l l a q a F C FA 2 6 2 2 0 0 0 S = − = − l q a a a q l l a q a MC FA a 2 3 6 6 3 0 0 0 = − = − 思考: 是否可以将梁上的分布荷载全部用静力等效后的 合力代替来求截面C的内力? FSC MC FA a A a/3 l q x q x 0 ( ) =

Ⅱ、剪力方程和弯矩方程·剪力图和弯矩图反映梁的横截面上的剪剪力方程Fs = Fs(x)力和弯矩随截面位置变弯矩方程M = M(x)化的函数式显示剪力和弯矩随截面位移的变化规律的图形则分别称为剪力图和弯矩图
Ⅱ、剪力方程和弯矩方程•剪力图和弯矩图 显示剪力和弯矩随截面位移的变化规律的图形则 分别称为剪力图和弯矩图。 ( ) S S F = F x M = M (x) 剪力方程 弯矩方程 反映梁的横截面上的剪 力和弯矩随截面位置变 化的函数式

例4-4图示悬臂梁受集度为g的满布均布荷载作用,试作梁的剪力图和弯矩图。PxA1解:1、以自由端为坐标原点,则可不求反力列剪力方程和弯矩方程:M(x)纯理维维室RF,(x)= qx(0 ≤x<1)xFs(x)xqxM()--x-2--(0≤x<l)M2
例4-4 图示悬臂梁受集度为q的满布均布荷载作用。 试作梁的剪力图和弯矩图。 解:1、以自由端为坐标原点,则可不求反力 列剪力方程和弯矩方程: F (x) = qx(0 x l) S ( ) ( x l) x qx M x = −qx = − 0 2 2 2 A B x l B x FS (x) M(x)

2、作剪力图和弯矩图F,(x)= qxqxBAM(x) = --2IFs0Fs,max = qlX82q12M.max1/22x注意:IM弯矩图中正的弯矩值绘在x轴的下方(即弯矩值绘在弯曲时梁的受拉侧)
2、 作剪力图和弯矩图 注意: 弯矩图中正的弯矩值绘在x轴的下方(即弯矩值绘在 弯曲时梁的受拉侧)。 F (x) = qx S ( ) 2 2 qx M x = − x ql FS ql 2 2 x M l/2 ql 2 8 A B l F = ql S,max 2 2 max ql M =