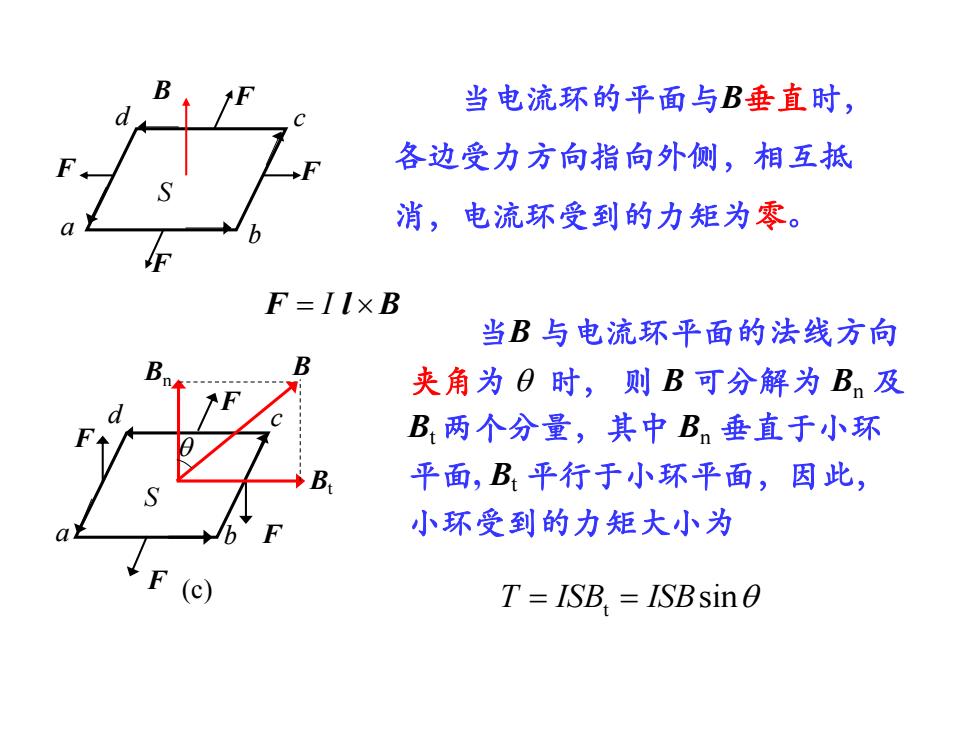
当电流环的平面与B垂直时,各边受力方向指向外侧,相互抵FS消,电流环受到的力矩为零。IFF=IlxB当B与电流环平面的法线方向BB夹角为 时,则B可分解为B,及dB两个分量,其中B,垂直于小环F平面,B平行于小环平面,因此,BS小环受到的力矩大小为aT = ISB, = ISBsin0
F d c b a F F B F S d c a b F F B B n Bt F F S (c) 当电流环的平面与B垂直时, 各边受力方向指向外侧,相互抵 消,电流环受到的力矩为零。 当B 与电流环平面的法线方向 夹角为 时, 则 B 可分解为 Bn 及 Bt两个分量,其中 Bn 垂直于小环 平面, Bt 平行于小环平面,因此, 小环受到的力矩大小为 T ISBt ISBsin F I l B

若定义有向面S的方向与电流方向构成右旋关系,则上式可写成失量形式T = I(S×B)可以证明,此式适用于任何形状的小电流环。通常,乘积IS称为小电流环的磁矩,以m表示,即m= IS则前式又可写为T=mxB此式表明,当m//B时,力矩为零;当mlB时,力矩最大
若定义有向面 S 的方向与电流方向构成右旋关系, 则上式可写成矢量形式 T I(S B) 可以证明,此式适用于任何形状的小电流环。通常, 乘积 IS 称为小电流环的磁矩,以 m表示,即 m IS 则前式又可写为 T mB 此式表明,当 时,力矩为零;当 时, 力矩最大。 m // B m B

磁通密度B通过某一表面S的通量称为磁通,以Φ表示,即@=[Bds磁通的单位为Wb(韦)磁通密度也可用一系列有向曲线来表示。曲线上某点的切线方向为磁通密度失量的方向,这些曲线称为磁场线。磁场线的矢量方程为B×dl = 0磁场线也不可相交。与电场线一样,若以磁场线构成磁场管,且规定相邻磁场管中的磁通相等,则磁场线的疏密程度也可表示磁场的强弱,磁场线密表示磁通密度大
磁通密度也可用一系列有向曲线来表示。曲线上某 点的切线方向为磁通密度矢量的方向,这些曲线称为磁 场线。磁场线的矢量方程为 B dl 0 磁场线也不可相交。与电场线一样,若以磁场线构 成磁场管,且规定相邻磁场管中的磁通相等,则磁场线 的疏密程度也可表示磁场的强弱,磁场线密表示磁通密 度大。 磁通密度 B 通过某一表面 S 的通量称为磁通,以 表示,即 B dS S 磁通的单位为Wb(韦)

磁场力已知F= Idl x B12112那么,由回路电流Ⅱ产生的dlr磁场B对于电流元Idl的作dl2用力dF21为r2ydF,, = I,dl, × BB1对于整个回路12的作用力F21因此,为I,dl, ×[1,d, ×(r, -r)]$,!F21 =4元91.12[r2 -rlB,(r)= od Ldl x(z -n)式中磁通密度B为4元1[r2 -ril
磁场力 已知 F Idl B 21 2 2 1 dF I dl B 式中磁通密度B1为 1 0 1 1 2 1 1 3 2 1 d ( ) ( ) 4π l I l r r B r r r 因此, B1 对于整个回路 l2 的作用力F21 为 1 2 0 2 2 1 1 2 1 21 3 2 1 d [ d ( )] 4π l l I I l l r r F r r 那么,由回路电流 I1 产生的 磁场 B1对于电流元 I2dl 的作 用力 dF21为 dl1 O z y x dl2 l2 l1 I2 I1 r2 - r1 r2 r1

同理,回路电流12产生的磁场B,对于整个回路I的作用力F12 为Fiz =ddx[d, ×(-)]4元9,[ri -r/上述两式称为安培定律。根据牛顿定律得知,应该F,=-F2。也可直接由上式获得证明。如果回路形状复杂,上述积分计算是很困难的。为了计算磁场力,类似计算电场力一样,也可采用虚位移方法,利用能量关系可以获得计算磁场力的简便方式。下面直接利用前述广义力和广义坐标的概念,导出计算磁场力的一般公式
同理,回路电流 I2 产生的磁场 B2 对于整个回路 l1 的作用力F12 为 1 2 0 1 1 2 2 1 2 12 3 1 2 d [ d ( )] 4π l l I I l l r r F r r 上述两式称为安培定律。 根据牛顿定律得知,应该 。也可直接由 上式获得证明。 F21 F12 如果回路形状复杂,上述积分计算是很困难的。 为了计算磁场力,类似计算电场力一样,也可采用虚 位移方法,利用能量关系可以获得计算磁场力的简便方式。 下面直接利用前述广义力和广义坐标的概念,导出 计算磁场力的一般公式