
第二章晶体振荡器概述 在谐振时并联RLC网络退化为一个简单的电阻R,因此谐振时平均功耗为: Pn-hcaR (2.8) 所以该网络在谐振时的Q值为: Q=Wo EtoL=WoRC= (2.9) Pavg LIC 同理,串联谐振时电感两端的峰值电流为lpeak,此时电感储能为 Eu-L (2.10) 2 所以串联RLC网络在谐振时的Q值为: Q=“4、1 (2.11) R w RC 注意到晶体模型中的电感非常大而电容非常小,将晶体模型中的串联LC 参数带入式(2.9)中可以估算出晶体的品质因数,可以高达10e。 2.3振荡器的分析方法 2.3.1反馈系统分析 Vout F(jw) 图2-4振荡器的正反馈模型 如图2-4所示,放大器的增益AGw)是频率的函数,反馈网络的增益为F(w), 也是频率的函数。若使电路能够正常振荡,在输入Vn为零的情况下,信号V 经过环路AGw)F(w)后的信号V:必须维持原信号的大小来维持振荡.放大网络为 非线性有源网络,反馈网络为线性无源网络,且具有选频特性,能够对单一频率 的噪声信号进行放大。据此,该系统起振的巴克豪森必要条件为 =A(wF(w≥1 (2.12) 告=,+,=0 这两个条件是形成振荡的必要条件但并非充分条件。由于存在着工艺和温度 的变化,为了确保振荡,电路在设计时通常将环路增益取为3。电路不可避免的 9
第二章 晶体振荡器概述 9 在谐振时并联 RLC 网络退化为一个简单的电阻 R,因此谐振时平均功耗为: 2 avg peak 1 2 P IR (2.8) 所以该网络在谐振时的 Q 值为: tot 0 0 avg / E R Q ω ω RC P L C (2.9) 同理,串联谐振时电感两端的峰值电流为 Ipeak,此时电感储能为 2 tot peak 1 2 E LI (2.10) 所以串联 RLC 网络在谐振时的 Q 值为: 0 0 ω L 1 Q R ω RC (2.11) 注意到晶体模型中的电感非常大而电容非常小,将晶体模型中的串联 RLC 参数带入式(2.9)中可以估算出晶体的品质因数,可以高达 10e6 。 2.3 振荡器的分析方法 2.3.1 反馈系统分析 图 2-4 振荡器的正反馈模型 如图 2-4 所示,放大器的增益 A(jω)是频率的函数,反馈网络的增益为 F(jω), 也是频率的函数。若使电路能够正常振荡,在输入 Vin 为零的情况下,信号 VƐ 经过环路 A(jω)F(jω)后的信号 Vf 必须维持原信号的大小来维持振荡。放大网络为 非线性有源网络,反馈网络为线性无源网络,且具有选频特性,能够对单一频率 的噪声信号进行放大。据此,该系统起振的巴克豪森必要条件为 f ε f A F ε ( )( )1 Φ Φ 0 V A jw F jw V V V (2.12) 这两个条件是形成振荡的必要条件但并非充分条件。由于存在着工艺和温度 的变化,为了确保振荡,电路在设计时通常将环路增益取为 3。电路不可避免的

差分结构数字控制晶体振荡器设计 存在着内部噪声,经过选频网络之后的具有特定频率的噪声信号经过环路不断被 放大,信号通路上的各级电路会经历非线性并最终达到“饱和”,限制了最大振 幅,最终保持环路的增益为1维持振荡。 2.3.2阻抗分离法 除了基于反馈网络的传递函数分析法,巴克豪森准则还可以另一种更加直观 的方式来表述,即阻抗分离法,后者对分析由有源电路和无源电路两部分构成的 系统非常的直接和方便。 对于理想的电感电容谐振电路,在正常振荡状态下电路中储存的电磁能在L 和C之间以固定的频率做周期性的交换,相互完全补偿,自成独立系统,与外 部无能量交换。但是无损元件是很难实现的,振荡器等效模型中的R。表征了晶 体的能量损失,因此很自然的可以想到,如果存在一个负阻,与R,相互抵消, 即可使电路达到振荡的状态,这就为阻抗分离法提供了理论基础。 当对RLC并联电路施加电流脉冲激励时电路将会发生振荡,电阻R,将会使 振荡慢慢的衰减为零,但是根据阻抗分离法分析的结果,如果可以产生一个“负 阻R,”并将其并联在电路两端,即使RLC中的并联电阻为O,即可使振荡持续 维持下去。 图2-5RLC并联电路的脉冲响应 实际电路中的负阻可以通过有源器件来实现,因此对于一个振荡器电路,可 以将系统划分为正阻电路(耗能部分)和负阻电路(供能部分)来进行分析。 将放大器A(Gw)用电路阻抗Zr代替,反馈网络用谐振器的阻抗Zes代替, 如图2-6所示。在振荡器达到稳态之后,能量的交换和补偿发生于系统内部, 因而不需要外部输入,即系统的输入导纳为零: Yres +Ycir=0 (2.13) 10
差分结构数字控制晶体振荡器设计 10 存在着内部噪声,经过选频网络之后的具有特定频率的噪声信号经过环路不断被 放大,信号通路上的各级电路会经历非线性并最终达到“饱和”,限制了最大振 幅,最终保持环路的增益为 1 维持振荡。 2.3.2 阻抗分离法 除了基于反馈网络的传递函数分析法,巴克豪森准则还可以另一种更加直观 的方式来表述,即阻抗分离法,后者对分析由有源电路和无源电路两部分构成的 系统非常的直接和方便。 对于理想的电感电容谐振电路,在正常振荡状态下电路中储存的电磁能在 L 和 C 之间以固定的频率做周期性的交换,相互完全补偿,自成独立系统,与外 部无能量交换。但是无损元件是很难实现的,振荡器等效模型中的 Rp 表征了晶 体的能量损失,因此很自然的可以想到,如果存在一个负阻,与 Rp 相互抵消, 即可使电路达到振荡的状态,这就为阻抗分离法提供了理论基础。 当对 RLC 并联电路施加电流脉冲激励时电路将会发生振荡,电阻 Rp将会使 振荡慢慢的衰减为零,但是根据阻抗分离法分析的结果,如果可以产生一个“负 阻 Rp”并将其并联在电路两端,即使 RLC 中的并联电阻为 0,即可使振荡持续 维持下去。 图 2-5 RLC 并联电路的脉冲响应 实际电路中的负阻可以通过有源器件来实现,因此对于一个振荡器电路,可 以将系统划分为正阻电路(耗能部分)和负阻电路(供能部分)来进行分析。 将放大器 A(jω)用电路阻抗 Zcir 代替,反馈网络用谐振器的阻抗 Zres 代替, 如图 2-6 所示。在振荡器达到稳态之后,能量的交换和补偿发生于系统内部, 因而不需要外部输入,即系统的输入导纳为零: Y Y res cir 0 (2.13)

第二章晶体振荡器概述 11 -=0 Zres Zor (2.14) 乙+Z=0 (2.15) ZrosZcr Re(Zres +Zcir)=0 (2.16) Im(Zes +Zcir )=0 (2.17) Ycir+Yres res 图2-6振荡器的负阻模型 阻抗分离法采用实部和虚部的形式来取代振幅和相位的形式来表示巴克豪 森准则,实际上两种形式是相关的,式(2.16)确定了电路振荡所需要的最小增益, 式(2.17)则确定了振荡频率[7]。 2.4常见晶体振荡器的结构 从晶体的阻抗频率响应曲线可以看出,晶体在串联谐振点与并联谐振点之间 呈电感的特性,根据负阻模型的分析,适当的选择有源电路来抵消晶体模型中电 阻的能量损耗,并引入容性负载即可实现振荡。在实际应用中可以根据具体的应 用要求来选择晶体振荡器的结构。按照晶体振荡器输出方式的不同可以分为单端 晶体振荡器和差分晶体振荡器。 2.4.1单端晶体振荡器 CMOS工艺下的单管有源器件足以提供有效的增益使晶体起振,因此可以 从基本的单晶体管振荡器出发来讨论单端输出晶体振荡器结构。单晶体管振荡器 也被称为三点式振荡器,根据接地点的不同,单晶体管振荡器可进一步分为 Pierce,Colpitts和Santos结构。 Pierce振荡器中晶品体管的源极接地,晶体连接在栅极和漏极之间,在电路达 到稳态之后晶体表现为一个小的电阻,漏极和栅极的电压几乎相等,因此输出可 以由漏极或者栅极得到。偏置电路可以由一个电流源和一个栅极电压偏置实现, 结构比较简单,但是由于晶体并没有接地端,因此需要两个管脚外接晶体。 在Colpitts结构的振荡器中栅极接地,晶体连接在栅极和漏极之间,在漏极 获得输出振荡电压,但是由于晶体表现为一个小的电阻,因此漏极上只有很小的
第二章 晶体振荡器概述 11 res cir 1 1 0 Z Z (2.14) res cir res cir 0 Z Z Z Z (2.15) Re( ) 0 Z Z res cir (2.16) Im( ) 0 Z Z res cir (2.17) 图 2-6 振荡器的负阻模型 阻抗分离法采用实部和虚部的形式来取代振幅和相位的形式来表示巴克豪 森准则,实际上两种形式是相关的,式(2.16)确定了电路振荡所需要的最小增益, 式(2.17)则确定了振荡频率[7]。 2.4 常见晶体振荡器的结构 从晶体的阻抗频率响应曲线可以看出,晶体在串联谐振点与并联谐振点之间 呈电感的特性,根据负阻模型的分析,适当的选择有源电路来抵消晶体模型中电 阻的能量损耗,并引入容性负载即可实现振荡。在实际应用中可以根据具体的应 用要求来选择晶体振荡器的结构。按照晶体振荡器输出方式的不同可以分为单端 晶体振荡器和差分晶体振荡器。 2.4.1 单端晶体振荡器 CMOS 工艺下的单管有源器件足以提供有效的增益使晶体起振,因此可以 从基本的单晶体管振荡器出发来讨论单端输出晶体振荡器结构。单晶体管振荡器 也被称为三点式振荡器,根据接地点的不同,单晶体管振荡器可进一步分为 Pierce,Colpitts 和 Santos 结构。 Pierce 振荡器中晶体管的源极接地,晶体连接在栅极和漏极之间,在电路达 到稳态之后晶体表现为一个小的电阻,漏极和栅极的电压几乎相等,因此输出可 以由漏极或者栅极得到。偏置电路可以由一个电流源和一个栅极电压偏置实现, 结构比较简单,但是由于晶体并没有接地端,因此需要两个管脚外接晶体。 在 Colpitts 结构的振荡器中栅极接地,晶体连接在栅极和漏极之间,在漏极 获得输出振荡电压,但是由于晶体表现为一个小的电阻,因此漏极上只有很小的
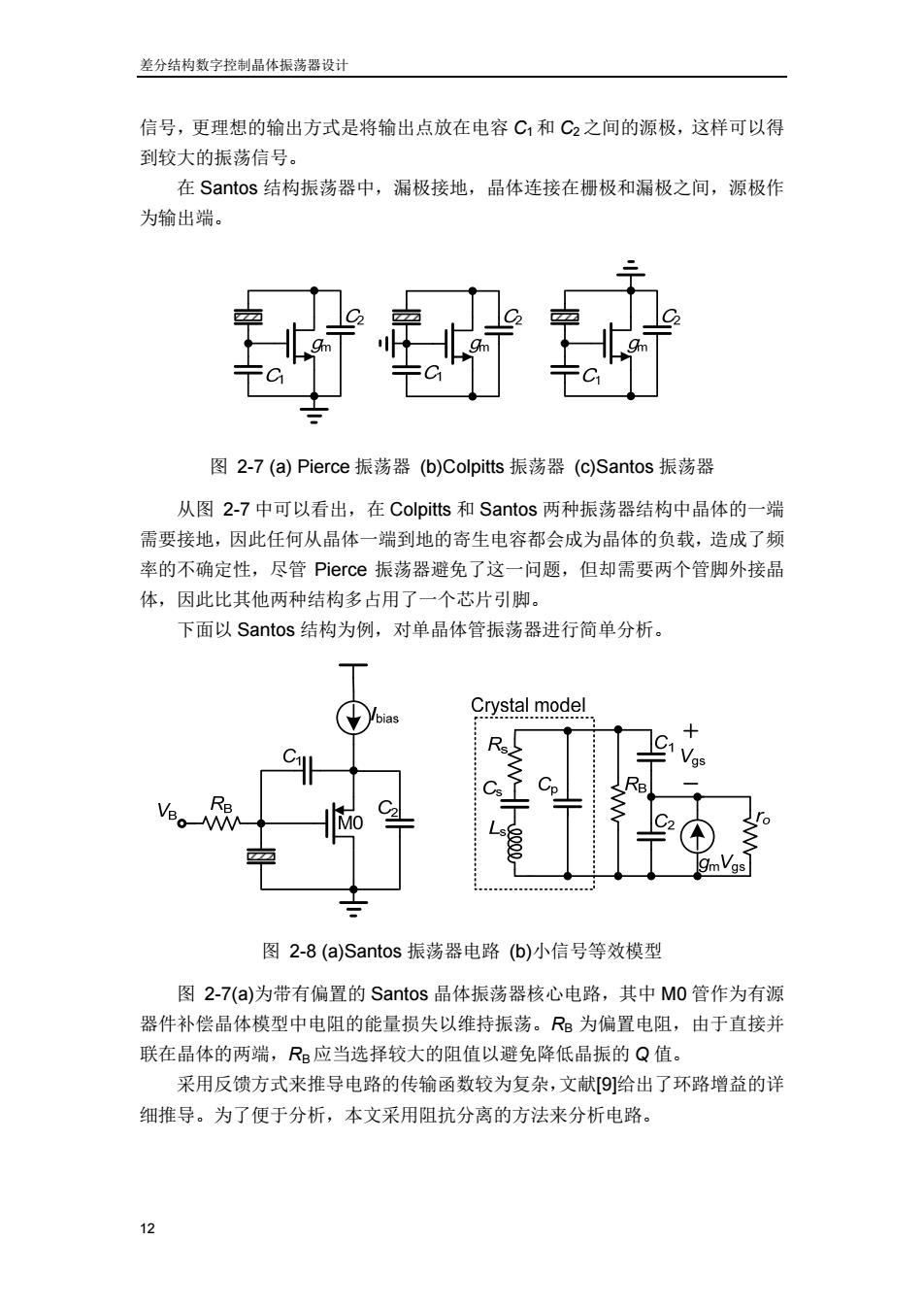
差分结构数字控制晶体振荡器设计 信号,更理想的输出方式是将输出点放在电容C1和C2之间的源极,这样可以得 到较大的振荡信号。 在Santos结构振荡器中,漏极接地,晶体连接在栅极和漏极之间,源极作 为输出端。 图2-7(a)Pierce振荡器(b)Colpitts振荡器(c)Santos振荡器 从图2-7中可以看出,在Colpitts和Santos两种振荡器结构中晶体的一端 需要接地,因此任何从晶体一端到地的寄生电容都会成为晶体的负载,造成了频 率的不确定性,尽管Pierce振荡器避免了这一问题,但却需要两个管脚外接晶 体,因此比其他两种结构多占用了一个芯片引脚。 下面以Santos结构为例,对单晶体管振荡器进行简单分析。 Crystal model VB。W c gmVgs 图2-8(a)Santos振荡器电路(b)小信号等效模型 图2-7(a)为带有偏置的Santos晶体振荡器核心电路,其中M0管作为有源 器件补偿晶体模型中电阻的能量损失以维持振荡。R:为偏置电阻,由于直接并 联在晶体的两端,R:应当选择较大的阻值以避免降低晶振的Q值。 采用反馈方式来推导电路的传输函数较为复杂,文献[⑨]给出了环路增益的详 细推导。为了便于分析,本文采用阻抗分离的方法来分析电路
差分结构数字控制晶体振荡器设计 12 信号,更理想的输出方式是将输出点放在电容 C1和 C2 之间的源极,这样可以得 到较大的振荡信号。 在 Santos 结构振荡器中,漏极接地,晶体连接在栅极和漏极之间,源极作 为输出端。 图 2-7 (a) Pierce 振荡器 (b)Colpitts 振荡器 (c)Santos 振荡器 从图 2-7 中可以看出,在 Colpitts 和 Santos 两种振荡器结构中晶体的一端 需要接地,因此任何从晶体一端到地的寄生电容都会成为晶体的负载,造成了频 率的不确定性,尽管 Pierce 振荡器避免了这一问题,但却需要两个管脚外接晶 体,因此比其他两种结构多占用了一个芯片引脚。 下面以 Santos 结构为例,对单晶体管振荡器进行简单分析。 图 2-8 (a)Santos 振荡器电路 (b)小信号等效模型 图 2-7(a)为带有偏置的 Santos 晶体振荡器核心电路,其中 M0 管作为有源 器件补偿晶体模型中电阻的能量损失以维持振荡。RB 为偏置电阻,由于直接并 联在晶体的两端,RB 应当选择较大的阻值以避免降低晶振的 Q 值。 采用反馈方式来推导电路的传输函数较为复杂,文献[9]给出了环路增益的详 细推导。为了便于分析,本文采用阻抗分离的方法来分析电路
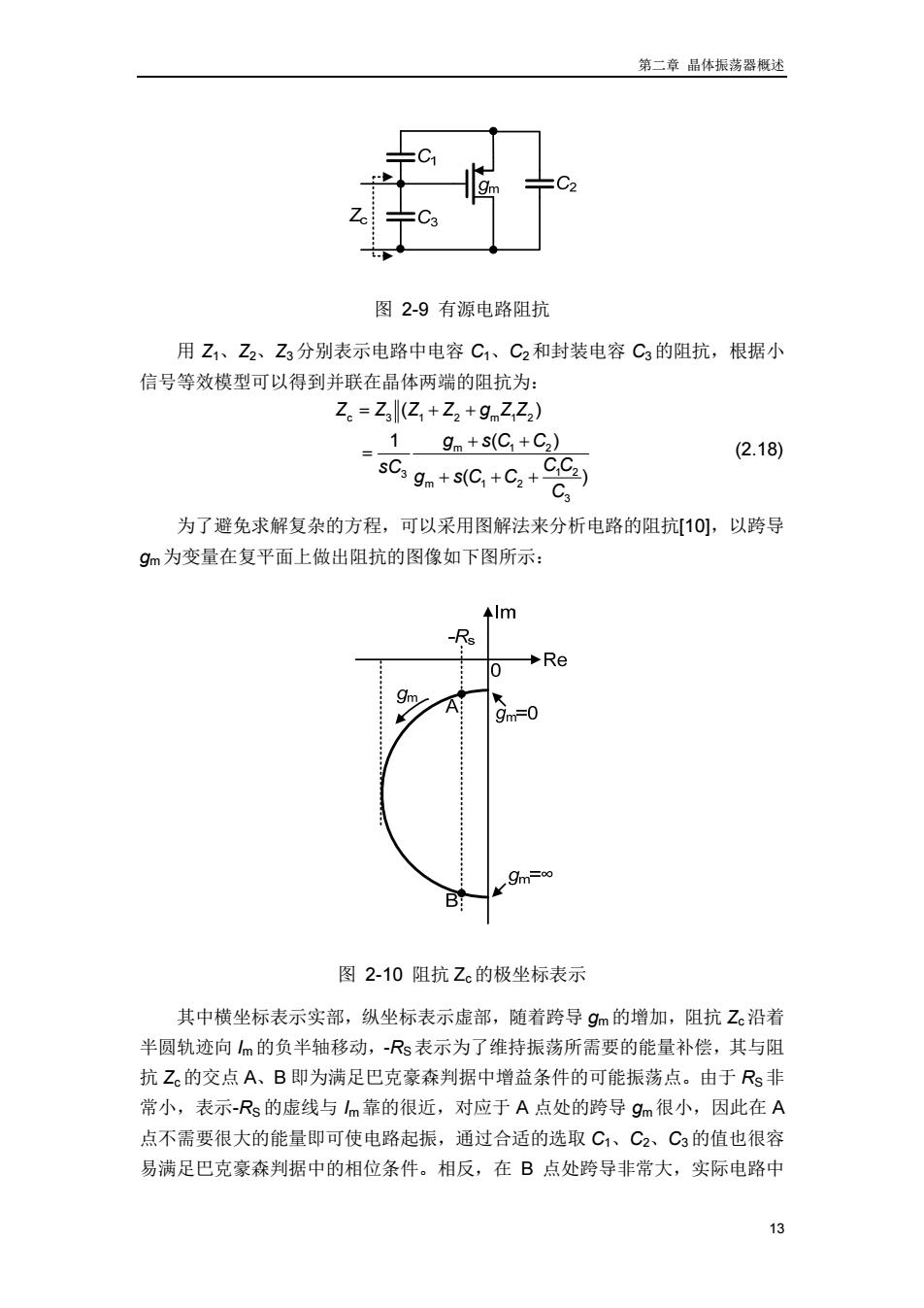
第二章晶体振荡器概述 图2-9有源电路阻抗 用Z1、Z2、Z3分别表示电路中电容C1、C2和封装电容C3的阻抗,根据小 信号等效模型可以得到并联在晶体两端的阻抗为: Z。=Z31(Z,+Z2+9mZ,Z2) 1 9m+s(C,+C2) (2.18) sCgn+sC,+C2+©e) C 为了避免求解复杂的方程,可以采用图解法来分析电路的阻抗[10],以跨导 gm为变量在复平面上做出阻抗的图像如下图所示: ◆m -Rs Re 0 9m A gm=0 gm=oo B: 图2-10阻抗Z。的极坐标表示 其中横坐标表示实部,纵坐标表示虚部,随着跨导9m的增加,阻抗Z。沿着 半圆轨迹向的负半轴移动,-Rs表示为了维持振荡所需要的能量补偿,其与阻 抗Z。的交点A、B即为满足巴克豪森判据中增益条件的可能振荡点。由于Rs非 常小,表示-Rs的虚线与Im靠的很近,对应于A点处的跨导gm很小,因此在A 点不需要很大的能量即可使电路起振,通过合适的选取C1、C2、C3的值也很容 易满足巴克豪森判据中的相位条件。相反,在B点处跨导非常大,实际电路中 13
第二章 晶体振荡器概述 13 图 2-9 有源电路阻抗 用 Z1、Z2、Z3分别表示电路中电容 C1、C2和封装电容 C3的阻抗,根据小 信号等效模型可以得到并联在晶体两端的阻抗为: c 3 1 2 m12 m 12 3 1 2 m 12 3 ( ) 1 ( ) ( ) Z Z Z Z g ZZ g sC C sC C C g sC C C (2.18) 为了避免求解复杂的方程,可以采用图解法来分析电路的阻抗[10],以跨导 gm为变量在复平面上做出阻抗的图像如下图所示: 图 2-10 阻抗 Zc 的极坐标表示 其中横坐标表示实部,纵坐标表示虚部,随着跨导 gm的增加,阻抗 Zc 沿着 半圆轨迹向 Im的负半轴移动,-RS表示为了维持振荡所需要的能量补偿,其与阻 抗 Zc 的交点 A、B 即为满足巴克豪森判据中增益条件的可能振荡点。由于 RS非 常小,表示-RS的虚线与 Im靠的很近,对应于 A 点处的跨导 gm很小,因此在 A 点不需要很大的能量即可使电路起振,通过合适的选取 C1、C2、C3 的值也很容 易满足巴克豪森判据中的相位条件。相反,在 B 点处跨导非常大,实际电路中