复旦大学：《集成电路工程》教学资源（硕士士学位论文）差分结构数字控制晶体振荡器设计

第一章概述 1.3论文组织结构 本文对通信系统常用的频率源一数字控制晶体振荡器的理论和实现进行了 系统的分析和研究，论文的具体组织结构如下： 第二章“晶体振荡器概述”简单介绍了晶体的特性及其电学等效模型，分析 了振荡器的基本原理和晶体振荡器的分类，同时对不同类型的晶体振荡器性能进 行了比较，提出了差分结构晶体振荡器所具有的优势。 第三章“可变电容特性分析”介绍了射频电路中常用的几种可变电容的类型， 详细分析了CMOS电容的结构及其电容一电压特性，通过大信号分析得到了其 周期内的等效电容值，阐述了调节可变电容能够进行频率控制的本质。 第四章“相位噪声分析”对线性时不变模型，非线性时不变模型和线性相位 时变模型进行了系统的阐述，对不同分析方法的优缺点进行了分析和比较，并采 用非线性时不变模型对振荡器的输出噪声进行了详细的分析。 第五章“差分结构晶体振荡器电路设计”给出了本次设计所采用的晶体参数， 根据应用需要分析了各项设计指标，并根据指标要求给出了在TSMC0.18um CMOS射频工艺上的数字控制晶体振荡器的设计实现及其仿真结果。 第六章“总结和展望”总结了本论文的工作，给出了今后需要进一步研究的 方向。 3

第一章 概述 3 1.3 论文组织结构 本文对通信系统常用的频率源—数字控制晶体振荡器的理论和实现进行了 系统的分析和研究，论文的具体组织结构如下： 第二章“晶体振荡器概述”简单介绍了晶体的特性及其电学等效模型，分析 了振荡器的基本原理和晶体振荡器的分类，同时对不同类型的晶体振荡器性能进 行了比较，提出了差分结构晶体振荡器所具有的优势。 第三章“可变电容特性分析”介绍了射频电路中常用的几种可变电容的类型， 详细分析了 CMOS 电容的结构及其电容—电压特性，通过大信号分析得到了其 周期内的等效电容值，阐述了调节可变电容能够进行频率控制的本质。 第四章“相位噪声分析”对线性时不变模型，非线性时不变模型和线性相位 时变模型进行了系统的阐述，对不同分析方法的优缺点进行了分析和比较，并采 用非线性时不变模型对振荡器的输出噪声进行了详细的分析。 第五章“差分结构晶体振荡器电路设计”给出了本次设计所采用的晶体参数， 根据应用需要分析了各项设计指标，并根据指标要求给出了在 TSMC 0.18 μm CMOS 射频工艺上的数字控制晶体振荡器的设计实现及其仿真结果。 第六章“总结和展望”总结了本论文的工作，给出了今后需要进一步研究的 方向

第二章晶体振荡器概述 第二章晶体振荡器概述 2.1晶体振荡器的分类 国际电工委员会(EC)将石英晶体振荡器分为四大类： 一是普通晶体振荡器(SPXO),即没有对频率漂移做任何补偿的晶体振荡器， 因其低廉的价格使其在温度变化不大或不需要精确频率源的电路中广泛应用。 二是电压控制品体振荡器(VCXO),电压控制晶体振荡器在较宽的线性调频 范围内具有良好的频率稳定度，因此通常应用于数字通讯、传输系统中。VCXO 具有频率稳定度高、调频范围宽、线性好等优点，因此适合应用于直接频率调制 电路中。 三是温度补偿式晶体振荡器(TCXO)。温度补偿式晶体振荡器是通过附加温 度补偿电路使得振荡频率随温度变化较小，由于具有体积小、重量轻、耗电少的 优点，广泛的应用于通讯、导航、通用仪器等电子设备中 四是恒温槽晶体振荡器(OCXO)。恒温槽晶体振荡器是通过恒温槽来使晶体 振荡器工作的环境温度保持恒定。根据具体的精度需求可以只将晶体置于恒温槽 中，也可将晶体和核心电路置于恒温槽中，还有的电路将晶体置于内部恒温槽中， 而将振荡电路置于外部的恒温槽中实现双重恒温槽控制。其频率的长期稳定性、 短期稳定性都很高，相位噪声小，但价格昂贵且功耗较大，适用于对频率稳定度 要求极高的电子设备及精密测量仪器中，由于结构限制，其体积和尺寸缩小的余 地非常有限。 近年来随着通讯系统中频率校正信道的出现以及芯片集成度的不断提高，可 以由集成数字基带产生频率控制码直接控制振荡器的负载电容阵列，从而实现对 频率的校正。数字控制晶体振荡器以其优良的性能在通讯系统中得到了广泛的应 用，并呈现出取代电压控制晶体振荡器的趋势。 2.2晶体谐振特性 石英晶体属于机械谐振腔，它的谐振依赖于外部施加的激励。由于晶体谐振 器有极高的频率稳定度和极低的功耗，被广泛的应用于频率控制和时钟电路中。 在实际应用中，晶体的切割方式，封装方式和振荡电路的设计都会对晶体的谐振 特性造成影响⑤]，因此需要在了解晶体的谐振特性及电学等效模型的基础上针对 不同的应用需求进行设计，尽管如此，在大多数应用中并不需要深入和全面的晶 体知识，因此本章节只介绍基本的晶体特性。 5

第二章 晶体振荡器概述 5 第二章 晶体振荡器概述 2.1 晶体振荡器的分类 国际电工委员会(IEC)将石英晶体振荡器分为四大类： 一是普通晶体振荡器(SPXO)，即没有对频率漂移做任何补偿的晶体振荡器， 因其低廉的价格使其在温度变化不大或不需要精确频率源的电路中广泛应用。 二是电压控制晶体振荡器(VCXO)，电压控制晶体振荡器在较宽的线性调频 范围内具有良好的频率稳定度，因此通常应用于数字通讯、传输系统中。VCXO 具有频率稳定度高、调频范围宽、线性好等优点，因此适合应用于直接频率调制 电路中。 三是温度补偿式晶体振荡器(TCXO)。温度补偿式晶体振荡器是通过附加温 度补偿电路使得振荡频率随温度变化较小，由于具有体积小、重量轻、耗电少的 优点，广泛的应用于通讯、导航、通用仪器等电子设备中 四是恒温槽晶体振荡器(OCXO)。恒温槽晶体振荡器是通过恒温槽来使晶体 振荡器工作的环境温度保持恒定。根据具体的精度需求可以只将晶体置于恒温槽 中，也可将晶体和核心电路置于恒温槽中，还有的电路将晶体置于内部恒温槽中， 而将振荡电路置于外部的恒温槽中实现双重恒温槽控制。其频率的长期稳定性、 短期稳定性都很高，相位噪声小，但价格昂贵且功耗较大，适用于对频率稳定度 要求极高的电子设备及精密测量仪器中，由于结构限制，其体积和尺寸缩小的余 地非常有限。 近年来随着通讯系统中频率校正信道的出现以及芯片集成度的不断提高，可 以由集成数字基带产生频率控制码直接控制振荡器的负载电容阵列，从而实现对 频率的校正。数字控制晶体振荡器以其优良的性能在通讯系统中得到了广泛的应 用，并呈现出取代电压控制晶体振荡器的趋势。 2.2 晶体谐振特性 石英晶体属于机械谐振腔，它的谐振依赖于外部施加的激励。由于晶体谐振 器有极高的频率稳定度和极低的功耗，被广泛的应用于频率控制和时钟电路中。 在实际应用中，晶体的切割方式，封装方式和振荡电路的设计都会对晶体的谐振 特性造成影响[5]，因此需要在了解晶体的谐振特性及电学等效模型的基础上针对 不同的应用需求进行设计，尽管如此，在大多数应用中并不需要深入和全面的晶 体知识，因此本章节只介绍基本的晶体特性

差分结构数字控制晶体振荡器设计 2.2.1晶体的压电特性 晶体谐振器是由一定厚度的压电效应物质，如石英(Quartz)、氧化锌或氮化 物构成，可以实现电能和机械能的相互转化。以石英晶体为例，在石英晶体的两 侧施加机械力，则会在晶体的两个极板之间产生一定的电场：反之，如果在晶体 的两极板之间施加电场，则会使晶体产生机械形变。如果在晶体两侧的基板上施 加交变电压，晶体就会产生机械振动，同时晶体的表面又会因为机械振动而产生 交变电场。 一般情况下，晶体机械振动的振幅和交变电场的振荡幅度是微小的，振动频 率稳定。当外压交变电压的频率与晶体的固有频率一致时，机械振动及其产生的 交变电场就会显著增大，称为压电谐振，此时的振荡频率称为晶体的谐振频率。 交变频率不同，晶体的振动强度不同，从而表现出对频率的选择性。 每个晶体都有自己的固有谐振频率，该频率同晶体的尺寸密切相关，晶体越 薄，固有振动频率越高。通常制作的晶体振荡器频率为100kHz到50MHz之间， 对于更高的频率，石英晶体则会变得太薄而易碎6]。 2.2.2晶体的电学等效模型及品质因子 谐振频率附近晶体的电学等效模型是串联的RCL电路，其谐振频率为∫s, 串联电阻为Rs,如图2-1所示。 Rs Ls 。。 ， Cp 图2-1晶体的电学等效模型 其中C。是连接晶体的两块平板之间的电容，也包括了封装电容和焊接电容， 数量级为pF,串联电容Cs在f数量级。从图2-1可以看出，电容Cp和Ls组 成了串联谐振电路，而封装电容C。和Ls组成了并联谐振电路，下面先从串、并 联谐振电路模型入手，进一步分析晶体的电学模型。 串联谐振和并联谐振的阻抗和导纳表达式分别为： C+jwL=R+1-WLC Z(ω)=R+1 (2.1) jwC Y(ω)=G+1 L +/wC=G+1-w*LC (2.2) jwL 从上式中可以看出，在频率非常低时，串联谐振表达式中的电容占主导地位 6

差分结构数字控制晶体振荡器设计 6 2.2.1 晶体的压电特性 晶体谐振器是由一定厚度的压电效应物质，如石英(Quartz)、氧化锌或氮化 物构成，可以实现电能和机械能的相互转化。以石英晶体为例，在石英晶体的两 侧施加机械力，则会在晶体的两个极板之间产生一定的电场；反之，如果在晶体 的两极板之间施加电场，则会使晶体产生机械形变。如果在晶体两侧的基板上施 加交变电压，晶体就会产生机械振动，同时晶体的表面又会因为机械振动而产生 交变电场。 一般情况下，晶体机械振动的振幅和交变电场的振荡幅度是微小的，振动频 率稳定。当外压交变电压的频率与晶体的固有频率一致时，机械振动及其产生的 交变电场就会显著增大，称为压电谐振，此时的振荡频率称为晶体的谐振频率。 交变频率不同，晶体的振动强度不同，从而表现出对频率的选择性。 每个晶体都有自己的固有谐振频率，该频率同晶体的尺寸密切相关，晶体越 薄，固有振动频率越高。通常制作的晶体振荡器频率为 100 kHz 到 50 MHz 之间， 对于更高的频率，石英晶体则会变得太薄而易碎[6]。 2.2.2 晶体的电学等效模型及品质因子 谐振频率附近晶体的电学等效模型是串联的 RCL 电路，其谐振频率为 ƒs， 串联电阻为 RS，如图 2-1 所示。 图 2-1 晶体的电学等效模型 其中 Cp是连接晶体的两块平板之间的电容，也包括了封装电容和焊接电容， 数量级为 pF，串联电容 Cs 在 fF 数量级。从图 2-1 可以看出，电容 Cp和 Ls 组 成了串联谐振电路，而封装电容 Cp和 Ls 组成了并联谐振电路，下面先从串、并 联谐振电路模型入手，进一步分析晶体的电学模型。 串联谐振和并联谐振的阻抗和导纳表达式分别为：     2 1 1 ( ) s ω LC Z ω R jωL R jωC jωC (2.1)     2 1 1 ( ) p ω LC Y ω G jωC G jωL jωL (2.2) 从上式中可以看出，在频率非常低时，串联谐振表达式中的电容占主导地位

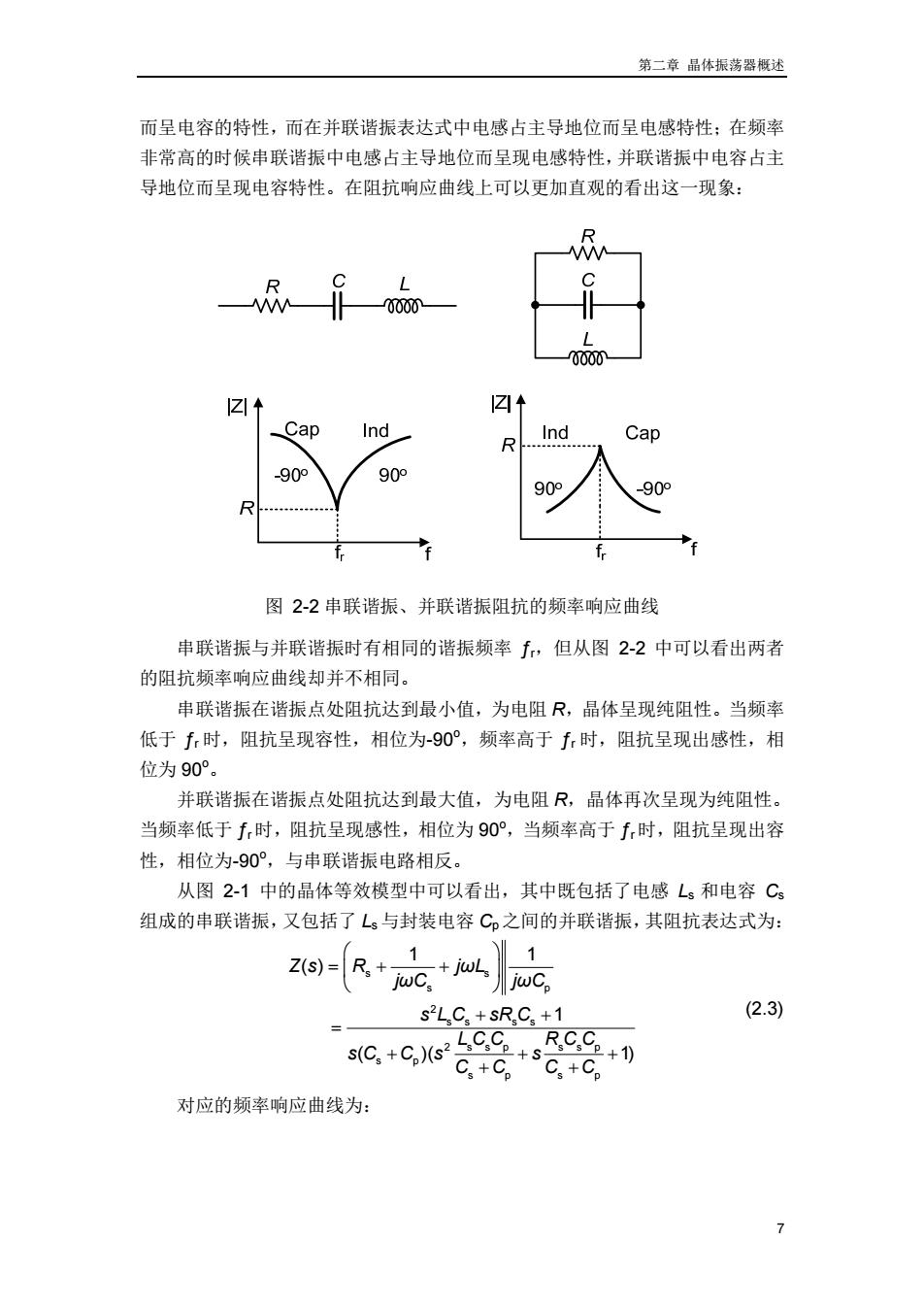
第二章晶体振荡器概述 而呈电容的特性，而在并联谐振表达式中电感占主导地位而呈电感特性；在频率 非常高的时候串联谐振中电感占主导地位而呈现电感特性，并联谐振中电容占主 导地位而呈现电容特性。在阻抗响应曲线上可以更加直观的看出这一现象： C 0000 L 00 Z ☑↑ Cap Ind Ind R Cap -90° 90° 90o -90° fr 图2-2串联谐振、并联谐振阻抗的频率响应曲线 串联谐振与并联谐振时有相同的谐振频率f,但从图2-2中可以看出两者 的阻抗频率响应曲线却并不相同。 串联谐振在谐振点处阻抗达到最小值，为电阻R,晶体呈现纯阻性。当频率 低于f,时，阻抗呈现容性，相位为-90°，频率高于f时，阻抗呈现出感性，相 位为90°。 并联谐振在谐振点处阻抗达到最大值，为电阻尺，晶体再次呈现为纯阻性。 当频率低于f,时，阻抗呈现感性，相位为90°，当频率高于时，阻抗呈现出容 性，相位为-90°，与串联谐振电路相反。 从图2-1中的晶体等效模型中可以看出，其中既包括了电感Ls和电容Cs 组成的串联谐振，又包括了Ls与封装电容C。之间的并联谐振，其阻抗表达式为： 1 jC。 S2L C+SR C+1 (2.3) S(C.+CN LCCRCC+0 C+C。C+C。 对应的频率响应曲线为：

第二章 晶体振荡器概述 7 而呈电容的特性，而在并联谐振表达式中电感占主导地位而呈电感特性；在频率 非常高的时候串联谐振中电感占主导地位而呈现电感特性，并联谐振中电容占主 导地位而呈现电容特性。在阻抗响应曲线上可以更加直观的看出这一现象： 图 2-2 串联谐振、并联谐振阻抗的频率响应曲线 串联谐振与并联谐振时有相同的谐振频率 ƒr，但从图 2-2 中可以看出两者 的阻抗频率响应曲线却并不相同。 串联谐振在谐振点处阻抗达到最小值，为电阻 R，晶体呈现纯阻性。当频率 低于 ƒr 时，阻抗呈现容性，相位为-90o ，频率高于 ƒr 时，阻抗呈现出感性，相 位为 90o 。 并联谐振在谐振点处阻抗达到最大值，为电阻 R，晶体再次呈现为纯阻性。 当频率低于 ƒr时，阻抗呈现感性，相位为 90o ，当频率高于 ƒr时，阻抗呈现出容 性，相位为-90o ，与串联谐振电路相反。 从图 2-1 中的晶体等效模型中可以看出，其中既包括了电感 Ls 和电容 Cs 组成的串联谐振，又包括了 Ls 与封装电容 Cp之间的并联谐振，其阻抗表达式为： s s s p 2 ss ss 2 ssp ssp s p sp sp 1 1 ( ) 1 ( )( 1) Zs R jωL jωC jωC s L C sR C LCC RCC sC C s s CC CC                 (2.3) 对应的频率响应曲线为：

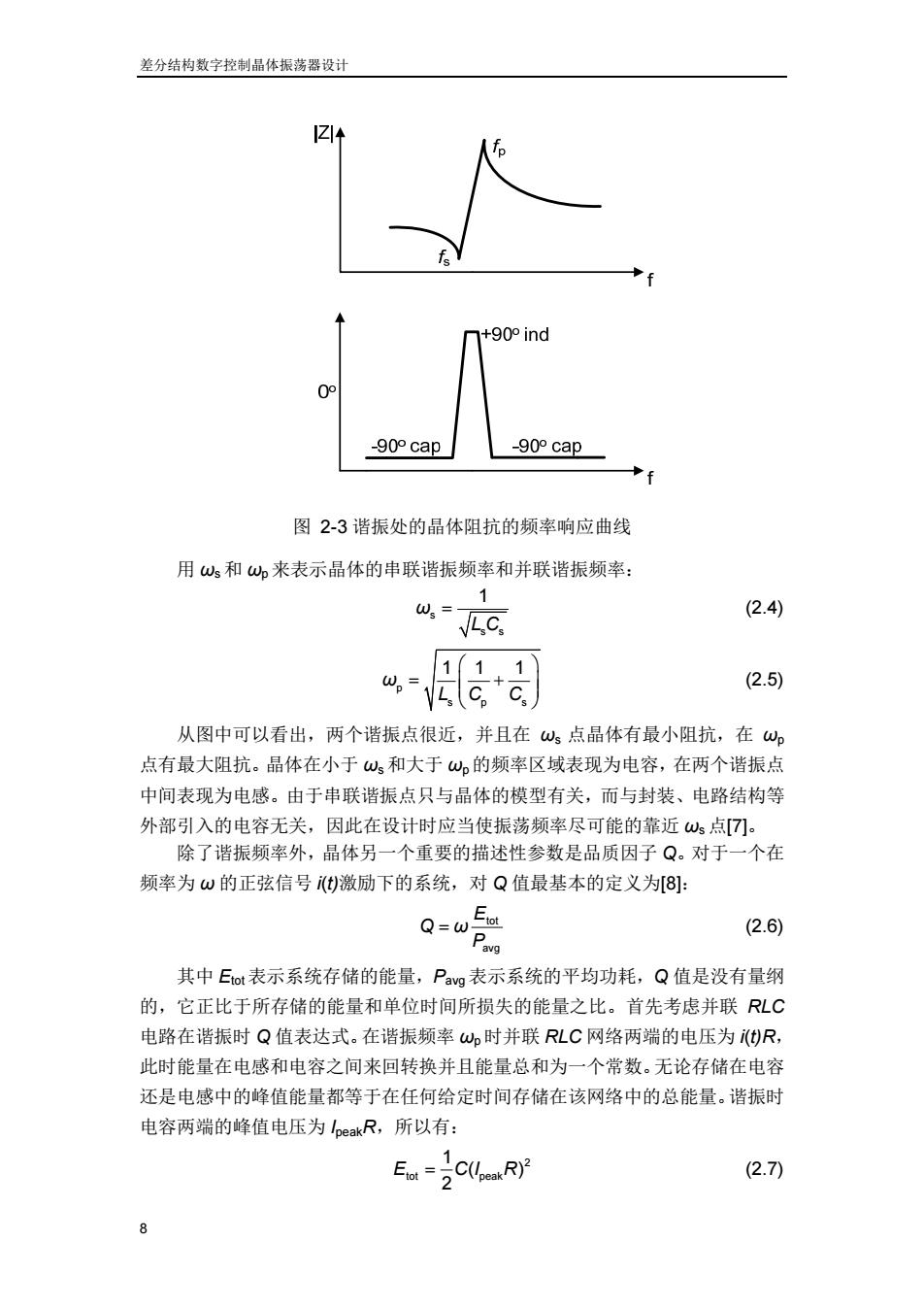
差分结构数字控制晶体振荡器设计 +90°ind 0° -90°cap -90°cap 图2-3谐振处的晶体阻抗的频率响应曲线 用ws和w来表示晶体的串联谐振频率和并联谐振频率： W3= (2.4) LC. 11,1 (2.5) 从图中可以看出，两个谐振点很近，并且在ω点晶体有最小阻抗，在w 点有最大阻抗。晶体在小于ω和大于ω。的频率区域表现为电容，在两个谐振点 中间表现为电感。由于串联谐振点只与晶体的模型有关，而与封装、电路结构等 外部引入的电容无关，因此在设计时应当使振荡频率尽可能的靠近s点[7]。 除了谐振频率外，晶体另一个重要的描述性参数是品质因子Q。对于一个在 频率为ω的正弦信号(t)激励下的系统，对Q值最基本的定义为[8]： Q=w ioL Pavg (2.6) 其中Eot表示系统存储的能量，Pavg表示系统的平均功耗，Q值是没有量纲 的，它正比于所存储的能量和单位时间所损失的能量之比。首先考虑并联RLC 电路在谐振时Q值表达式。在谐振频率wo时并联RLC网络两端的电压为(t)R, 此时能量在电感和电容之间来回转换并且能量总和为一个常数。无论存储在电容 还是电感中的峰值能量都等于在任何给定时间存储在该网络中的总能量。谐振时 电容两端的峰值电压为peakR,所以有： ECVR) (2.7) 8

差分结构数字控制晶体振荡器设计 8 图 2-3 谐振处的晶体阻抗的频率响应曲线 用 ωs 和 ωp来表示晶体的串联谐振频率和并联谐振频率： s  s s 1 ω L C (2.4)         p sp s 11 1 ω LC C (2.5) 从图中可以看出，两个谐振点很近，并且在 ωs 点晶体有最小阻抗，在 ωp 点有最大阻抗。晶体在小于 ωs 和大于 ωp的频率区域表现为电容，在两个谐振点 中间表现为电感。由于串联谐振点只与晶体的模型有关，而与封装、电路结构等 外部引入的电容无关，因此在设计时应当使振荡频率尽可能的靠近 ωs 点[7]。 除了谐振频率外，晶体另一个重要的描述性参数是品质因子 Q。对于一个在 频率为 ω 的正弦信号 i(t)激励下的系统，对 Q 值最基本的定义为[8]：  tot avg E Q ω P (2.6) 其中 Etot表示系统存储的能量，Pavg表示系统的平均功耗，Q 值是没有量纲 的，它正比于所存储的能量和单位时间所损失的能量之比。首先考虑并联 RLC 电路在谐振时 Q 值表达式。在谐振频率 ωp时并联 RLC 网络两端的电压为 i(t)R， 此时能量在电感和电容之间来回转换并且能量总和为一个常数。无论存储在电容 还是电感中的峰值能量都等于在任何给定时间存储在该网络中的总能量。谐振时 电容两端的峰值电压为 IpeakR，所以有：  2 tot peak 1 ( ) 2 E CI R (2.7)