
Properties of the electron density p()is a non-negative function depending on only three variables .p()vanishes at infinity and integrates to the total number of electrons N: limp()=0 →0 p(di=N p()can be measured experimentally (e.g.by X-ray diffraction) at the position of atoms,the gradient of p()has a discontinuity: l层+2z6=0 Z being the nuclear charge and p()the spherical average of p() decays exponentially for large distances from nuclei p()~exp(-2v2) I being the exact first ionization energy of the system Function:y=f(x) p=p(xy,Z) Functional:y=F[f(x)] E=F[p(x,y,z)]
Properties of the electron density Function: y=f(x) ρ = ρ(x,y,z) Functional: y=F[f(x)] E=F[ ρ(x,y,z)]
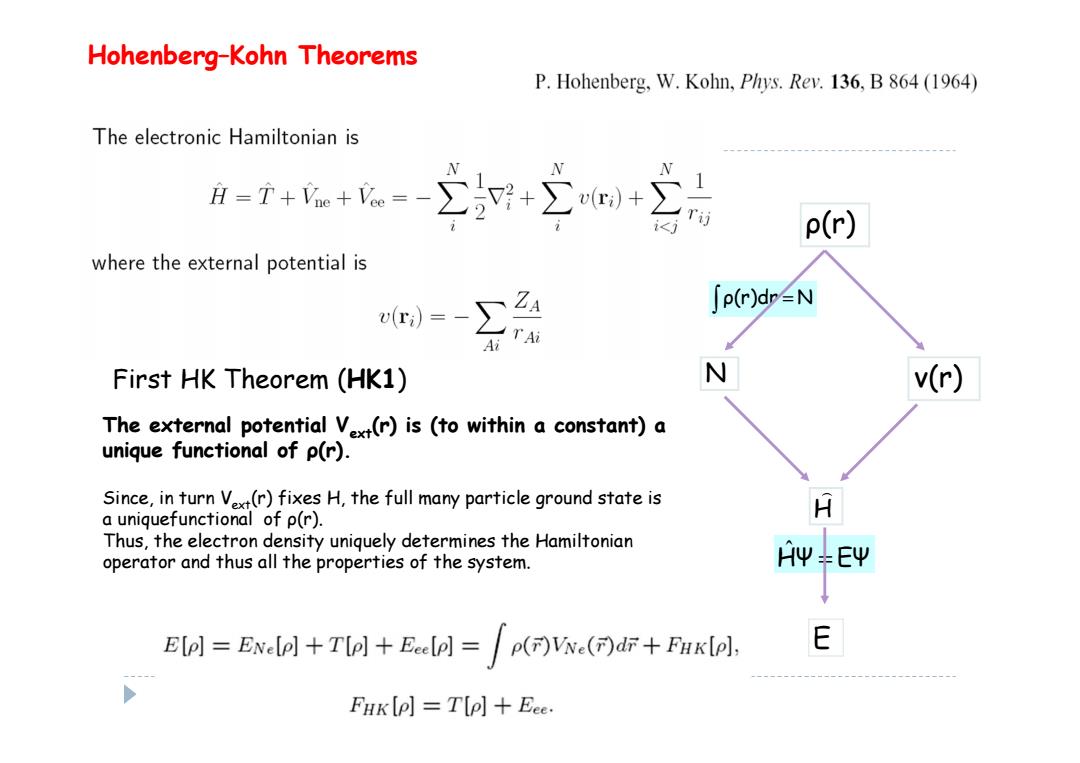
Hohenberg-Kohn Theorems P.Hohenberg,W.Kohn,Phys.Rev.136,B 864 (1964) The electronic Hamiltonian is A=T++=-∑+∑+ i p(r) where the external potential is r)=-∑24 ∫p(rdr2N Ai T Ai First HK Theorem (HK1) N v(r) The external potential Vx(r)is (to within a constant)a unique functional of p(r). Since,in turn Vext(r)fixes H,the full many particle ground state is a uniquefunctional of p(r). A Thus,the electron density uniquely determines the Hamiltonian operator and thus all the properties of the system. AΨ+EΨ Elo]=ENe+Tol+Eeeel =()Vx()dr+Fuklol, E FHK (P]T(p]Eee
ρ(r) ν(r) H E N ρ(r)dr = N HΨ = EΨ ˆ First HK Theorem (HK1) Hohenberg–Kohn Theorems The external potential Vext(r) is (to within a constant) a unique functional of ρ(r). Since, in turn Vext(r) fixes H, the full many particle ground state is a uniquefunctional of ρ(r). Thus, the electron density uniquely determines the Hamiltonian operator and thus all the properties of the system

A=T+V+Va→平→D←平=F=T+V+V 儿 E 国 Proof: 4'as a test function for H: E。< (平'平= =ΨΨ+(平-Ψ E。< E6+(Ψ'T+Ve+Vet-i-Ve-V|平 E。< E+p(F){Ves-Ves}dr Y as a testfunction for H': Eo<Eo-p(F)[Ves-Ves}dr Summing up the last two inequalities: E+E%<E+E。 Contradiction!
Ψ’ as a test function for H: Ψ as a testfunction for H’: Summing up the last two inequalities: Proof: Contradiction!

Eo[Po]=T[Po]+Eee[Po]+ENe[Po]. Eo[Po]=|Po(F)VNedi T[Po]+Eee[Po] system dependent univgfsally valid Eo[Po]=Po()VNedi +Fik[po] FHk??? Fak[p]=T[p]+E.[p]=(T+Vw E1-50@+5l=+E的

E[p]=ENe [p]+T[p]+Eee [p]=p(r)VNe (F)dr +FK[p] with f4K[pl=I可 Eee -打8d+5回5西 Only J[p]is known! The explicit form of T[p]and EnnLp]is the major challenge of DFT contains all the effects of self-interaction correction and exchange and Coulomb correlation